在图搜索算法中,如果按估价函数f(x)=g(x)+h(x)作为OPEN表中的结点排序的依据,则该算法就是深度优先算法。
题目
在图搜索算法中,如果按估价函数f(x)=g(x)+h(x)作为OPEN表中的结点排序的依据,则该算法就是深度优先算法。
相似考题
参考答案和解析
更多“在图搜索算法中,如果按估价函数f(x)=g(x)+h(x)作为OPEN表中的结点排序的依据,则该算法就是深度优先算法。”相关问题
-
第1题:
设函数f(x)为奇函数,g(x)为偶函数,则复合函数()是奇函数。A.f(f(x))
B.g(f(x))
C.f(g(x))
D.g(g(x))
正确答案:A
-
第2题:
阅读下列函数说明和C代码,将应填入(n) 处的字句写在对应栏内。
【说明】
函数print(BinTreeNode*t; DateType &x)的功能是在二叉树中查找值为x的结点,并打印该结点所有祖先结点。在此算法中,假设值为x的结点不多于一个。此算法采用后序的非递归遍历形式。因为退栈时需要区分右子树。函数中使用栈ST保存结点指针ptr以及标志tag,Top是栈顶指针。
【函数】
void print( BinTreeNode * t; DateType &x) {
stack ST; int i, top; top = 0;//置空栈
while(t! = NULL &&t-> data!= x || top!=0)
{ while(t!= NULL && t-> data!=x)
{
/*寻找值为x的结点*/
(1);
ST[top]. ptr = t;
ST[top]. tag = 0;
(2);
}
if(t!= Null && t -> data == x) { /*找到值为x的结点*/
for(i=1;(3);i ++)
printf("%d" ,ST[top]. ptr ->data);
else {
while((4))
top--;
if(top>0)
{
ST[top]. tag = 1;
(5);
}
}
}
正确答案:(1)top++ (2)t=t->leftChild (3)i=top (4)top>0 && ST[top].tag=1 (5)t=ST[top].ptr->rightChild
(1)top++ (2)t=t->leftChild (3)i=top (4)top>0 && ST[top].tag=1 (5)t=ST[top].ptr->rightChild 解析:这个程序是一个典型二叉树后序遍历非递归算法的应用。算法的实现思路是:先扫描根结点的所有左结点并入栈;当找到一个结点的值为x,则输入出栈里存放的数据,这些数据就是该结点所有祖先结点;然后判断栈顶元素的右子树是否已经被后序遍历过,如果是,或者右子树为空,将栈顶元素退栈,该子树已经全部后序遍历过;如果不是,则对栈顶结点的右子树进行后序遍历,此时应把栈顶结点的右子树的相结点放入栈中。再重复上述过程,直至遍历过树中所有结点。
(1)、(2)空年在循环就是扫描根结点的所有左结点并入栈,根据程序中的栈的定义,栈空时top=0,因此在入栈时,先将栈顶指针加1,因此(1)空处应填写“top++”或其等价形式,(2)空是取当前结点的左子树的根结点,因此应填写“t=t->leftChild”。
(3)空所在循环是处理找到值为x的结点,那么该结点的所有祖先结点都存放在栈中,栈中的栈底是二叉树的根,而栈顶元素是该结点的父结点,因此,(3)空处应填写“i=top”。
(4)空所在循环是判断栈顶元素的右子树是否已经被后序遍历过,如果是,或者右子树为空,将栈顶元素退栈,这里要填写判断条件。 tag=0表示左子树,tag=1表示右子树,因此,(4)空处应填写“top> 0&&ST [top].tag=1”。
(5)空所在语句块是处理栈顶元素的右子树没有被后序遍历情况,则将右子树入栈,因此(5)空处应填写“t=ST[top].ptr->rightChild”。 -
第3题:
如果求一个连通图中以某个顶点为根的高度最小的生成树,应采用()A、深度优先搜索算法
B、广度优先搜索算法
C、求最小生成树的prim算法
D、拓扑排序算法
参考答案:B
-
第4题:
设f(x)为偶函数,g(x)为奇函数,则下列函数中为奇函数的是( )。A. f[g(x)]
B. f[f(x)]
C. g[f(x)]
D. g[g(x)]答案:D解析:D项,令T(x)=g[g(x)]。因为T(-x)=g[g(-x)]=g[-g(x)]=-g[g(x)],所以T(-x)=-T(x),所以g[g(x)]为奇函数。 -
第5题:
设函数f(x),g(x)是大于零的可导函数,且f′(x)g(x)-f(x)g′(x)<0,则当a<x<b时有( )《》( )A.f(x)g(b)>f(b)g(x)
B.f(x)g(a)>f(a)g(x)
C.f(x)g(x)>f(b)g(b)
D.f(x)g(x)>f(a)g(a)答案:A解析: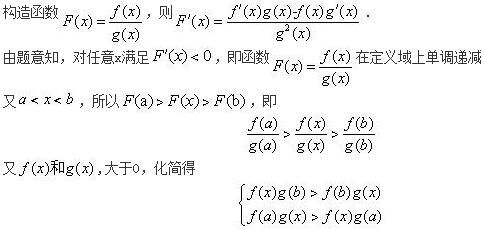
-
第6题:
在A算法中,当h(n)≡0时,则A算法演变为()
- A、爬山法
- B、动态规划法
- C、A*算法
- D、深度优先算法
正确答案:B -
第7题:
如果问题存在最优解,则下面几种搜索算法中,()必然可以得到该最优解
- A、广度优先搜索
- B、深度优先搜索
- C、有界深度优先搜索
- D、启发式搜索
正确答案:A -
第8题:
利用评价函数f(n)=g(n)+h(n)来排列OPEN表节点顺序的图搜索算法称为()
- A、深度优先算法
- B、宽度优先算法
- C、盲搜索算法
- D、A算法
正确答案:D -
第9题:
单选题如果问题存在最优解,则下面几种搜索算法中,()可以认为是“智能程度相对比较高”的算法A广度优先搜索
B深度优先搜索
C有界深度优先搜索
D启发式搜索
正确答案: A解析: 暂无解析 -
第10题:
单选题利用评价函数f(n)=g(n)+h(n)来排列OPEN表节点顺序的图搜索算法称为()A深度优先算法
B宽度优先算法
C盲搜索算法
DA算法
正确答案: A解析: 暂无解析 -
第11题:
单选题设函数f(x),g(x)在[a,b]上均可导(a<b),且恒正,若f′(x)g(x)+f(x)g′(x)>0,则当x∈(a,b)时,下列不等式中成立的是( )。[2018年真题]Af(x)/g(x)>f(a)/g(b)
Bf(x)/g(x)>f(b)/g(b)
Cf(x)g(x)>f(a)g(a)
Df(x)g(x)>f(b)g(b)
正确答案: C解析:
因为[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)>0,所以函数f(x)g(x)在[a,b]上单调递增。所以,当x∈(a,b)时,f(a)g(a)<f(x)g(x)<f(b)g(b)。 -
第12题:
问答题设函数f(x),g(x)二次可导,满足函数方程f(x)g(x)=1,又f′(x)≠0,g′(x)≠0,则f″(x)/f′(x)-f′(x)/f(x)=g″(x)/g′(x)-g′(x)/g(x)。正确答案:
f(x)g(x)=1,则f′(x)g(x)+f(x)g′(x)=0①
即f′(x)/f(x)=-g′(x)/g(x)②
对①两边求导得f″(x)g(x)+2f′(x)g′(x)+f(x)g″(x)=0,即f″(x)+2f′(x)g′(x)/g(x)+f(x)g″(x)/g(x)=0,即f″(x)/f′(x)+2f′(x)g′(x)/f′(x)g(x)+f(x)g″(x)/f′(x)g(x)=0。
由①得f″(x)/f′(x)+2g′(x)/g(x)-f(x)g″(x)/f(x)g′(x)=0,则f″(x)/f′(x)+2g′(x)/g(x)=g″(x)/g′(x)。
又由②得f″(x)/f′(x)-f′(x)/f(x)=g″(x)/g′(x)-g′(x)/g(x)。解析: 暂无解析 -
第13题:
如果问题存在最优解,则下面几种搜索算法中,()必然可以得到该最优解。A.广度优先搜索
B.深度优先搜索
C.有界深度优先搜索
D.启发式搜索
答案:A
-
第14题:
图的遍历算法有深度优先搜索算法和广度优先搜索算法。()此题为判断题(对,错)。
正确答案:√
-
第15题:
图的深度优先搜索算法类似于二叉树的(51)。
A.前序遍历
B.中序遍历
C.后序遍历
D.按层次遍历
正确答案:A
解析:深度优先搜索是从图中某个顶点V出发,访问此顶点,然后依次从V的未被访问的邻接点出发深度优先遍历图,直至图中所有和V有路径相通的顶点都被访问到。深度搜索遍历类似于树的先根遍历,是树的先根遍历的推广,所以答案为A。同理,由广度优先搜索遍历的定义可知其类似于按层次遍历的过程。 -
第16题:
设函数f(x),g(x)在[a,b]上均可导(a<b),且恒正,若f′(x)g(x)+f(x)g′(x)>0,则当x∈(a,b)时,下列不等式中成立的是( )。A. [f(x)/g(x)]>[f(a)/g(b)]
B. [f(x)/g(x)]>[f(b)/g(b)]
C. f(x)g(x)>f(a)g(a)
D. f(x)g(x)>f(b)g(b)答案:C解析:因为[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)>0,所以函数f(x)g(x)在[a,b]上单调递增。所以,当x∈(a,b)时,f(a)g(a)<f(x)g(x)<f(b)g(b)。 -
第17题:
若函数f(x)=(k-1)ax- ax (a>0且α≠1)在R上既是奇函数,又是减函数,则g(x)=loga (x+k)的图象是( )。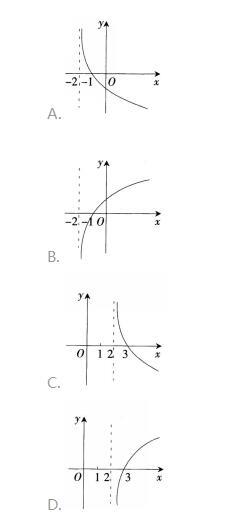 答案:A解析:函数f(x)是奇函数,则有f(0)=(k-1)-1=0,得k=2.f(x)=ax-a-x。又f(x)在R上是减函数,则有0
答案:A解析:函数f(x)是奇函数,则有f(0)=(k-1)-1=0,得k=2.f(x)=ax-a-x。又f(x)在R上是减函数,则有0第18题:
如果问题存在最优解,则下面几种搜索算法中,()可以认为是“智能程度相对比较高”的算法
- A、广度优先搜索
- B、深度优先搜索
- C、有界深度优先搜索
- D、启发式搜索
正确答案:D第19题:
广度优先搜索算法中,OPEN表的数据结构实际是一个二叉树,深度优先搜索算法中,OPEN表的数据结构实际是一个()。
正确答案:单链表第20题:
在F[x]中,有f(x)+g(x)=h(x)成立,若将x用矩阵A代替,将有f(A)+g(A)≠h(A)。
正确答案:错误第21题:
单选题设f(x)为偶函数,g(x)为奇函数,则下列函数中为奇函数的是()。Af[g(x)]
Bf[f(x)]
Cg[f(x)]
Dg[g(x)]
正确答案: D解析:第22题:
单选题如果问题存在最优解,则下面几种搜索算法中,( )必然可以得到该最优解。A广度优先搜索
B深度优先搜索
C有界深度优先搜索
D启发式搜索
正确答案: B解析:
广度优先搜索中,若问题有解,则可找到最优解,其他搜素不具有此特点,所以选择A项。第23题:
填空题广度优先搜索算法中,OPEN表的数据结构实际是一个二叉树,深度优先搜索算法中,OPEN表的数据结构实际是一个()。正确答案: 单链表解析: 暂无解析第24题:
单选题设f(x)为偶函数,g(x)为奇函数,则下列函数中为奇函数的是( )。[2018年真题]Af[g(x)]
Bf[f(x)]
Cg[f(x)]
Dg[g(x)]
正确答案: C解析:
D项,令T(x)=g[g(x)]。因为T(-x)=g[g(-x)]=g[-g(x)]=-g[g(x)],所以T(-x)=-T(x),所以g[g(x)]为奇函数。
