设X~N（1,2)，则3X+4服从A．N(0,1)B．N(7,18)C．N(3,18)D．N(7,6)

题目

设X~N（1,2)，则3X+4服从

A．N(0,1)

B．N(7,18)

C．N(3,18)

D．N(7,6)

相似考题

1.设X~N(0,1),Y~N(0,1),且X与Y相互独立,则X＋Y服从的分布为()A、X+Y服从N(0，1)B、X+Y不服从正态分布C、X+Y~X2(2)D、X+Y也服从正态分布

2.X服从标准正态分布(0,1),则Y=1＋2X的分布是:()A、N(1,2);B、N(1,4)C、N(2,4);D、N(2,5)。

3.设随机变量X服从正态分布N（2，4），Y服从均匀分布U（3，5），则E（2X-3Y）= __________.

4.设X~N(3,42),且Y=3X＋4,则DY等于()。A、27B、25C、144D、43

参考答案和解析
错误
更多“设X~N（1,2)，则3X+4服从”相关问题

  • 第1题：

    设X服从正态分布N(0,4),则E[x(x－2)]=()

    A、2

    B、4

    C、0

    D、1


    答案：B

    解析：

            E[x(x-2)]

        =    E(x2)-E(2x)

        =    E(x2)

        =    (E(x))2+D(x)

        =    D(x)

        =    4

  • 第2题：

    设Xi(i＝1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。

    A．若Xi(i＝1，2，…，n)服从正态分布，且分布参数相同，则服从正态分布

    B．若Xi(i＝1，2，…，n)服从指数分布，且λ相同，则服从正态分布

    C．若Xi(i＝1，2，…，n)服从[a，b]上的均匀分布，则服从正态分布

    D．无论Xi(i＝1，2，…，n)服从何种相同的分布，其均值都服从正态分布


    正确答案：D
    解析：中心极限定理指出，无论共同的分布是什么，只要随机变量的个数n相当大时，的分布总近似于正态分布。

  • 第3题：

    设X,Y相互独立且都服从分布N(0,4),则( ).


    答案：B
    解析：

  • 第4题：

    设总体X服从分布N(0，2^2)，而X1，X2，…，X15是来自总体X的简单随机样本，则随机变量服从_______分布，参数为________.


    答案：1、F 2、(10，5)
    解析：
    本题是数三的考题，由于X～N(0，2^2)，则　
    且相互独立，故

    答案应填服从F分布，参数为(10，5).

  • 第5题：

    设随机变量X～N(1,2),Y～N(-1,2),Z～N(0,9)且随机变量X,Y,Z相互独立,已知a(X+Y)2＋bZ2～χ2(n)(ab≠O),则a=_______,b=_______,Z=_______.


    答案：
    解析：
    由X～N(1，2)，Y～N(-1，2)，Z～N(0，9)，得X+Y～N(0，4)，且，故.

  • 第6题：

    设二维随机变量(X，Y)服从正态分布N(μ，μ；σ^2，σ^2；0)，则E(XY^2)=________.


    答案：
    解析：

  • 第7题：

    设随机变量X服从正态分布N（1，2），Y服从泊松分布P（2）。求期望E=（2X—y+3）。


    答案：
    解析：
    解：本题考查一些重要分布的数字特征与参数之间的关系。E（X）=1，E（y）=2 E（2X-y+3）=2E（X）-E（y）+3=3。

  • 第8题：

    设（X1，X2，…，X）是抽自正态总体N（0，1）的一个容量为n的样本，记，则下列结论中正确的是（）。

    • A、服从正态分布N（0，1）
    • B、n服从正态分布N（0，1）
    • C、服从自由度为n的x2分布
    • D、服从自由度为（n-1）的t分布

    正确答案:C

  • 第9题：

    设随机变量X与Y相互独立，且X~N（1，2），Y~N（0，1）。令Z=-Y+2X+3，则D（Z）=（）。


    正确答案:9

  • 第10题：

    设某质量特性X服从正态分布N(μ,σ),则P(︱X-μ︱≥3σ)等于（）。

    • A、973%
    • B、2700ppm
    • C、63ppm
    • D、0027

    正确答案:B,C

  • 第11题：

    设X服从N（0，4），则E[X（X-2）]=（）。

    • A、2
    • B、4
    • C、0
    • D、1

    正确答案:B

  • 第12题：

    设随机变量X服从正态分布N（μ，16），Y服从正态分布N（μ，25）.记p=P（X≤μ-4），g=P（Y≥μ+5），则p与q的大小关系是（）．

    • A、p>q
    • B、p
    • C、p=q
    • D、不能确定

    正确答案:C

  • 第13题：

    设X～N(μ，σ2)，σ未知，xi为样本(i=1，2，…，n)。H0:μ≤μ0，H1:μ＞μ0，α为显著性水平，则接受域( )。


    正确答案：C
    解析：对单侧要求的假设检验，σ未知，采用t检验，检验统计量，拒绝域为，所以接受域为。

  • 第14题：

    设X～t(2),则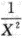服从的分布为( ).

    A.χ^2(2)
    B.F(1,2)
    C.F(2,1)
    D.χ^2(4)

    答案：C
    解析：
    因为X～t(2)，所以存在U～N(0，1)，V～χ^2(2)，且U，V相互独立，使得，则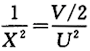，因为V～χ^2(2)，U^2～χ^2(1)且V，U^2相互独立，所以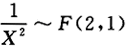，选(C).

  • 第15题：

    设X~N(μ，σ2)，σ已知，xi为样本（i= 1，2，…，n）。 H0：μ=μ0 ， H1：μ≠μ0 ，则检验统计量指的是（ ）。


    答案：B
    解析：
    对于单个正态总体，当总体方差σ2已知时，均值μ的检验统计量为。

  • 第16题：

    设随机变量X在［-1,2］上服从均匀分布,随机变量=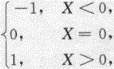则D(Y)=_______.


    答案：
    解析：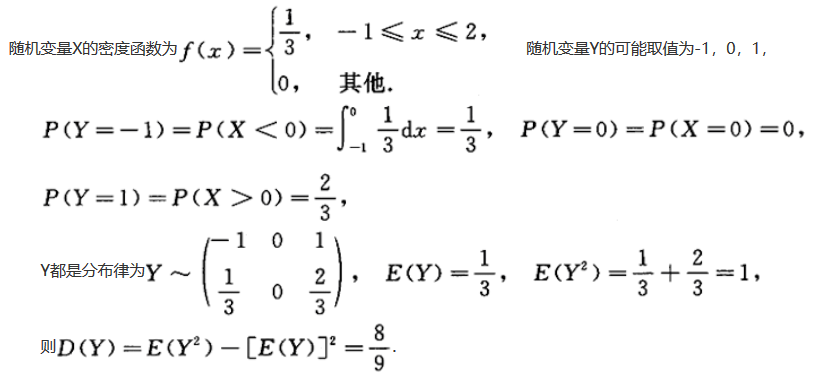

  • 第17题：

    设X1,2X,…,Xn（n>2）相互独立且都服从N(0,1),Yi=Xi-X（i=1,2,…,n）.求：
    　　(1)D(Yi)(i=1,2,…,n);(2)Cov(Y1,Yn);(3)P(Yn+Yn≤0).


    答案：
    解析：

  • 第18题：

    设随机变量X服从N（0，2），则（ ）。



    答案：D
    解析：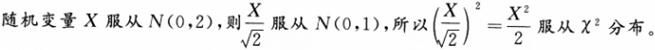

  • 第19题：

    设un≤vn(n=1，2，…)，则（）



    答案：D
    解析：
    un、vn可能为任意数值，因此正项级数的比较判别法不能成立，可知应选D．

  • 第20题：

    设随机变量X服从以n，p为参数的二项分布，且EX=15，DX=10，则n=（）。


    正确答案:45

  • 第21题：

    设X为服从正态分布N（-1，2）的随机变量，则E（2X-1）=（）。

    • A、9
    • B、6
    • C、4
    • D、-3

    正确答案:D

  • 第22题：

    设随机变量X服从正态分布N（-1，9），则随机变量Y=2-X服从（）．

    • A、正态分布N（3，9）
    • B、均匀分布
    • C、正态分布N（1，9）
    • D、指数分布

    正确答案:A

  • 第23题：

    设随机变量X服从N（-1，4），则P｛X+1＜0｝=（）


    正确答案:0.5

  • 第24题：

    单选题
    设X～N（0，1），则X2服从（）．
    A

    χ2（n）

    B

    χ2（1）

    C

    t（1）

    D

    N（0，1）


    正确答案： B
    解析： 暂无解析

相关内容