掷一枚硬币，观察其出现的是正面还是反面，并将事件A定义为：事件A=出现正面，这一事件的概率记作P（A)。则概率P（A)=1/2的含义是（）。A．抛掷多次硬币，出现正面的次数接近一半B．抛掷多次硬币，恰好有一半结果正面朝上C．抛掷两次硬币，恰好有一次结果正面朝上D．掷一次硬币，出现的恰好是正面

题目

掷一枚硬币，观察其出现的是正面还是反面，并将事件A定义为：事件A=出现正面，这一事件的概率记作P（A)。则概率P（A)=1/2的含义是（）。

A．抛掷多次硬币，出现正面的次数接近一半

B．抛掷多次硬币，恰好有一半结果正面朝上

C．抛掷两次硬币，恰好有一次结果正面朝上

D．掷一次硬币，出现的恰好是正面

相似考题

1.掷硬币两次，事件“全是正面或全是反面”的概率是( )。A．1/4B．1/2C．3/4D．1

2.一枚硬币掷3次,出现两次或两次以上正面的概率是()。A.0.1B.0.9C.0.8D.0.5

3.一枚硬币投掷三次，或三枚硬币各掷一次，出现两次或两次以上正面的概率是1/2。()

4.掷均匀硬币一次,事件“出现正面或反面”的概率为________。A．0.1B．0.5C．0.4D．1

参考答案和解析
B
更多“掷一枚硬币，观察其出现的是正面还是反面，并将事件A定义为：事件A=出现正面，这一事件的概率记作P（A)。则概率P（A)=1/2的含义是（）。”相关问题

  • 第1题：

    抛掷一枚硬币，观察其出现正面或反面的过程，就是随机试验，“正面向上”就是随机事件。()


    参考答案：正确

  • 第2题：

    将一枚匀称的硬币连续掷两次，则正面只出现一次的概率为()

    A、1/3

    B、0.5

    C、0.6

    D、0.1


    参考答案：B


  • 第3题：

    关于频率与概率有下列几种说法
    ①“明天下雨的概率是90％”，表示明天下雨的可能性很大
    ②“抛一枚硬币正面朝上的概率为50％”，表示每抛两次硬币就有一次正面朝上
    ③“某彩票中奖的概率是1％”，表示买10张该种彩票不可能中奖
    ④“抛一枚硬币正面朝上的概率为50％”，表示随着抛掷硬币次数的增加，“抛出正面朝上”这一事件发生的频率稳定在50％附近
    其中正确的说法是()。

    A.①④
    B.②③
    C.④
    D.①③

    答案：A
    解析：
    事件A的概率P(A)是对事件A发生可能性大小的一个度量，它是一个确定的数值，与试

  • 第4题：

    计算以下事件的概率可以用古典概率方法解决的是()。

    A:明天是晴天的概率
    B:抛一枚硬币出现正面的概率
    C:明天股票上涨的概率
    D:某地发生交通事故的概率

    答案：B
    解析：
    可以使用古典概率方法计算概率的事件需具备三个条件：事件可能产生的结果是有限的，所有结果之间两两互不相容的，所有的结果发生都是等可能的。依据这三个条件，只有B项符合。

  • 第5题：

    随机投一枚硬币共10次，其中3次为正面，7次为反面。则该随机事件（ ）为3/10。

    A：出现正面的频数
    B：出现正面的频率
    C：出现正面的概率
    D：出现正面的可能性

    答案：B
    解析：

  • 第6题：

    掷一枚均匀的硬币若干次，当正面向上次数大于反面向上次数时停止，则在4次之内停止的概率为



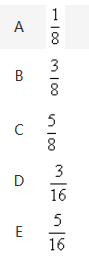    答案：C
    解析：

  • 第7题：

    掷均勻硬币一次，事件“出现正面或反面”的概率为（ ）。
    A. 0. 1 B. 0.4 C. 0. 5 D. 1


    答案：D
    解析：
    掷硬币一次，不是出现正面，就是出现反面，所以事件“出现正面或反面”为必然事件，其概率为1。

  • 第8题：

    将一枚硬币独立地掷两次，引进事件：A1={掷第一次出现正面}，A2={掷第二次出现正面}，A3={正、反面各出现一次}，A4={正面出现两次}，则事件（）

    • A、A1，A2，A3相互独立
    • B、A2，A3，A4相互独立
    • C、A1，A2，A3两两独立
    • D、A2，A3，A4两两独立

    正确答案:C

  • 第9题：

    一枚硬币被投掷三次并且三次都是正面，第四次试验出现正面的概率（）

    • A、比出现背面的概率小
    • B、比出现背面的概率大
    • C、是1/16
    • D、是1/2

    正确答案:D

  • 第10题：

    单选题
    掷硬币两次，事件“全是正面或全是反面”的概率是（　　）。
    A

    1/4

    B

    1/2

    C

    3/4

    D

    1


    正确答案： A
    解析： 掷硬币两次，样本空间为{（正面，正面），（正面，反面），（反面，正面），（反面，反面）}，故“全是正面或全是反面”的概率为2/4＝1/2。

  • 第11题：

    单选题
    掷均匀硬币一次，事件“出现正面或反面”的概率为（　　）。
    A

    0.1

    B

    0.4

    C

    0.5

    D

    1


    正确答案： B
    解析： 掷硬币一次，不是出现正面，就是出现反面，所以事件“出现正面或反面”为必然事件，其概率为1。

  • 第12题：

    单选题
    随机投一枚硬币共10次，其中3次为正面，7次为反面。则该随机事件（）为3/10。
    A

    出现正面的频数

    B

    出现正面的频率

    C

    出现正面的概率

    D

    出现正面的可能性


    正确答案： C
    解析： 暂无解析

  • 第13题：

    相继掷硬币两次，则样本空间为

    A、Ω={(正面,反面),(反面,正面),(正面,正面),(反面,反面)}

    B、Ω={(正面,反面),(反面,正面)}

    C、{(正面,反面),(反面,正面),(正面,正面)}

    D、{(反面,正面),(正面,正面)}


    参考答案：A


  • 第14题：

    （2）连续4次抛掷一枚硬币，求恰出现两次是正面的概率和最后两次出现是正面的概率。


    正确答案：
              

  • 第15题：

    扔一枚质地均匀的硬币，我们知道出现正面或反面的概率都是0.5，这属于概率应用方法中的()。

    A:古典概率方法
    B:统计概率方法
    C:主观概率方法
    D:样本概率方法

    答案：A
    解析：

  • 第16题：

    如下事件发生的概率等于1/4的是()。

    A:抛两枚普通的硬币，出现的均是正面
    B:一个不透明的袋子里装着黑白红蓝四种颜色的球，随机拿出一个恰好为红色球
    C:抛两枚普通的硬币，出现一个正面和一个反面
    D:掷一枚普通的骰子，出现点数小于3
    E:掷两枚普通的骰子，出现点数之和小于

    答案：A,B
    解析：
    A选项，出现两个都是正面的概率=1/2*1/2=1/4；B选项，考查古典概率计算方法的使用，随机拿出一个球可能有4种颜色，红色只占其中一种，所以拿出恰为红色球的概率=1/4；C选项，出现一个正面和一个反面应该包括两种情况：正反、反正，因此其概率=1/4+1/4=1/2；D选项，掷出的点数总共有6种情况，而小于3的只有l和2两种情况，所以其概率=2/6=1/3；E选项，掷两枚骰子，出现的点数和最小为2，即两枚骰子的点数都是1，因此其和小于2是不可能事件，所以概率=0。

  • 第17题：

    随机投一枚硬币共10 次，其中3 次为正面， 7 次为反面。则该随机事件( )为3/10，

    A.出现正面的频数
    B. 出现正面的频率
    C. 出现正面的概率
    D.出现正面的可能性

    答案：B
    解析：

  • 第18题：

    一枚硬币掷三次，出现两次正面在上的概率是

    A.0.25
    B.0.375
    C.0.50
    D.0.625

    答案：B
    解析：
    一枚硬币掷三次，有八种情况，分别是正正正，正正反，正反正，正反反，反正正，反反正，反正反，反反反。根据概率乘法规则计算，每种情况出现的概率是1/2x1/2x1/2= 1/8。再根据加法法则，两次正面在上的概率为3/8。

  • 第19题：

    扔一枚硬币，正反面出现的概率相等，任一面朝上这一事件所获得的自信息量是（）。

    • A、1/2
    • B、-log（1/2）
    • C、-1
    • D、-log1

    正确答案:B

  • 第20题：

    对掷一枚硬币的试验，“出现正面”称为（）。

    • A、随机事件
    • B、必然事件
    • C、不可能事件
    • D、样本空间

    正确答案:A

  • 第21题：

    下列关于概率的说法，正确的是（）

    • A、事件M发生的概率0＜P（M）＜1
    • B、若事件M确定发生，则P（M）=1
    • C、事件M发生的概率0＜P（M）≤1
    • D、若事件M不确定发生，则P（M）=0

    正确答案:B

  • 第22题：

    单选题
    下列关于概率的说法，正确的是（）
    A

    事件M发生的概率0＜P（M）＜1

    B

    若事件M确定发生，则P（M）=1

    C

    事件M发生的概率0＜P（M）≤1

    D

    若事件M不确定发生，则P（M）=0


    正确答案： C
    解析： 暂无解析

  • 第23题：

    单选题
    将一枚硬币独立地掷两次，以A1、A2、A3、A4依次表示事件“第一次出现正面”，“第二次出现正面”、“正、反面各出现一次”，“正面出现两次”，则事件（　　）。
    A

    A1，A2，A3相互独立

    B

    A2，A3，A4相互独立

    C

    A1，A2，A3两两独立

    D

    A2，A3，A4两两独立


    正确答案： C
    解析：
    因为A4发生，则A1，A2必然发生，A2与A4不独立，从而排除B，D项；若A3发生则A1，A2中有且仅有一个发生，则A1，A2，A3不相互独立，故排除A项。

  • 第24题：

    单选题
    下列事件中，必然事件是(　　)．
    A

    掷一枚硬币出现正面    

    B

    掷一枚硬币出现反面

    C

    掷一枚硬币，或者出现正面，或者出现反面  

    D

    掷一枚硬币，出现正面和反面


    正确答案： A
    解析： 根据必然事件的定义可以知道

相关内容