在由两个不同组别消费者组成的市场1和市场2上，产量分别为Y1和Y2，消费者反需求函数为P1（Y1）和P2（Y2），用C（Y1+Y2）表示生产的成本，则在三级价格歧视下，厂商在两个市场上总产量分割满足什么条件时，以实现利润最大化。（）A.MC（Y1+Y2）=MR1（Y1）=MR2（Y2B.MR2（Y2）>MC（Y1+Y2）=MR1（Y1）C.MR1（Y1）>MC（Y1+Y2）=MR2（Y2）D.MR1（Y1）=MR2（Y2）=MC（Y1+Y2）

题目

在由两个不同组别消费者组成的市场1和市场2上，产量分别为Y1和Y2，消费者反需求函数为P1（Y1）和P2（Y2），用C（Y1+Y2）表示生产的成本，则在三级价格歧视下，厂商在两个市场上总产量分割满足什么条件时，以实现利润最大化。（）

A.MC（Y1+Y2）=MR1（Y1）=MR2（Y2

B.MR2（Y2）>MC（Y1+Y2）=MR1（Y1）

C.MR1（Y1）>MC（Y1+Y2）=MR2（Y2）

D.MR1（Y1）=MR2（Y2）=MC（Y1+Y2）

相似考题

1.有以下程序： float f1(float n) { return n*n； } float f2(float n) { return 2*n； } main() {float(*p1)(float)，(*p2)(float)，(*t)(float)，y1，y2； p1：f1; p2=f2； y1=p2(p1(2.0))； t=p1； p1=p2； p2=t； y2=p2(p1(2.0))； printf("%3.0f，%3.0f\n",y1,y2)； } 程序运行后的输出结果是 ______。A．8， 16B．8， 8C．16， 16D．4， 8

2.有以下程序:include float f1 (float n ){return n*n;}float f2 ( float n){return 2有以下程序:#include ＜stdio.h＞float f1 (float n ){ return n*n;}float f2 ( float n){ return 2 * n;}main( ){ float ( * p1)(float),( * p2)(float),(*t)(float) ,y1,y2; p1 = f1;p2 = f2; y1 = p2(p1(2.0) ); t =p1;p1 = p2;p2 =t; y2=p2(p1(2.0)); prinff("% 3.0f, %3.Of\n" ,y1,y2);}程序运行后的输出结果是( )。A．8,16B．8,8C．16,16D．4,8

3.已知二次函数y1=x2-x-2和一次函数y2=x+1的两个交点分别为A(-1，0)，B(3，4)，当y1＞y2时，自变量x的取值范围是（ ）A．x＜-1或x＞3 B．-1＜x＜3 C．x＜-1 D．x＞3

4.有以下程序 float fl(float n) { return n*n； } float f2(float n) { return 2*n；} main() {float(*p1)(float)，(*p2)(float)，(*t)(float)，y1，Y2； p1=f1； p2=f2； y1=p2(p1(2.O))； t=p1； p1=p2； p2=t； y2=p2(pl(2.0))； printf("%3.0f，%3，Of\n"，y1，y2)； } 程序运行后的输出结果是A．8，16B．8，8C．16，16D．4，8

参考答案和解析
参考答案：A
更多“在由两个不同组别消费者组成的市场1和市场2上，产量分别为Y1和Y2，消费者反需求函数为P1（Y1）和P2（Y ”相关问题

  • 第1题：

    设非齐次线性微分方程y′+P(x)y=Q(x)有两个不同的解y1(x)，y2(x)，C为任意常数，则该方程通解是( )。

    A.C[y1(x)-y2(x)]
    B.y1(x)+C[y1(x)-y2(x)]
    C.C[y1(x)+y2(x)]
    D.y1(x)+C[y1(x)+y2(x)]

    答案：B
    解析：
    因为y1(x)，y2(x)是y′+P(x)y=Q(x)的两个不同的解，所以C(y1(x)-y2(x))是齐次方程y′+P(x)y=0的通解，进而y1(x)+C[y1(x)-y2(x)]是题中非齐次方程的通解。

  • 第2题：

    在一个人（既是消费者又是生产者）的经济e={X，y，ω}中，商品1和商品2在消费和生产中分别满足下面的条件：X一{z∈R2 ▏x1≥2，x2≥0}Y={y∈R2▏y2≤2(-y1)2,y1≤0）。效用函数为U(x1，x2)-（x1-2）x2，初始资源禀赋为ω=(4，0)。 对于价格p=（p1，p2）∈R2++,写出生产者问题并求解最大化利润下的y1和y2。


    答案：
    解析：
    生产者问题可表述为：

    构造拉格朗日辅助函数： L=p1y1+p2 y2 +λ1(-y1)+λ2(2y12－y2) 根据K-T条件及经济学含义，得：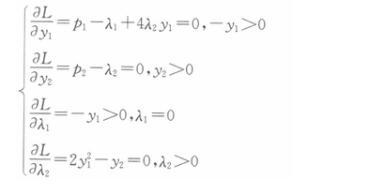

    解得：

  • 第3题：

    在一个人（既是消费者又是生产者）的经济e={X，y，ω}中，商品1和商品2在消费和生产中分别满足下面的条件：X一{z∈R2 ▏x1≥2，x2≥0}Y={y∈R2▏y2≤2(-y1)2,y1≤0）。效用函数为U(x1，x2)-（x1-2）x2，初始资源禀赋为ω=(4，0)。现在假设财富取决于初始禀赋和利润，请推导出商品1的市场均衡条件。假如此时p1=1，p2为多少？


    答案：
    解析：
    若财富取决于初始禀赋和利润，则此时w=4p1+P1 y1 +p2y2，将(1)中结果代入，得：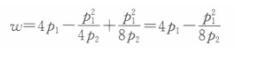

    将上式代入(2)中结果，得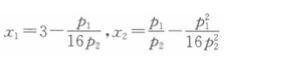

    商品1的市场均衡时，商品需求等于初始禀赋加上商品供给，即均衡条件为x1=ωx+y1，即： 当P1=1时，解得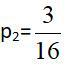

    综上，商品1达到市场均衡时，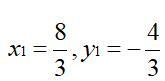

    假如此时p1=1，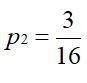

    那么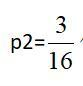

  • 第4题：

    设非齐次线性微分方程y´+P(x)y=Q(x)有两个不同的解析：y1(x)与y2(x)，C为任意常数，则该方程的通解是( ).

    A.C[(y1(x)-y2(x)]
    B.y1(x)+C[(y1(x)-y2(x)]
    C.C[(y1(x)+y2(x)]
    D.y1(x)+C[(y1(x)+y2(x)]

    答案：B
    解析：
    y1(x)-y2(x)是对应的齐次方程y

  • 第5题：

    在一个人（既是消费者又是生产者）的经济e={X，y，ω}中，商品1和商品2在消费和生产中分别满足下面的条件：X一{z∈R2 ▏x1≥2，x2≥0}Y={y∈R2▏y2≤2(-y1)2,y1≤0）。效用函数为U(x1，x2)-（x1-2）x2，初始资源禀赋为ω=(4，0)。假设财富满足ω≥2P1， 对于P=(p1，p2)∈R2++写出消费者问题并求解对x1和x2的需求量。


    答案：
    解析：
    消费者问题可表述为：

    构造拉格朗日辅助函数：L=(X1-2)X2+μ(ω-p1x1-p2x2) 利润最大化的一阶条件为：

    解得：

相关内容