简要说明消费函数。

题目

简要说明消费函数。

相似考题

1.简要说明网络经济下，消费者行为理论发生了哪些变化？

2.持久收入假说是如何说明消费函数的稳定性的？

3.简要说明消费函数的稳定性的意义。

4.生命周期假说是如何说明消费函数的稳定性的？

更多“简要说明消费函数。 ”相关问题

  • 第1题：

    假定： (a)消费函数为c=50+0.8y，投资函数为=100（亿美元）- 5r; (b)消费函数为c=50 +0. 8y，投资函数为=100（亿美元）- 1Or； (c)消费函数为c=50 +0. 75y，投资函数为i=100（亿美元）- 1Or。 (1)求(a)、(b)、(c)的IS曲线。 (2)比较(a)和(b)，说明投资对利率更敏感时，IS曲线的斜率发生什么变化。 (3)比较(b)和(c)，说明边际消费倾向变动时，IS曲线的斜率发生什么变化。


    答案：
    解析：
    (1)根据y=c+s，得到s=y-c=y-(50+0.8y)=-50+0.2y，再根据均衡条件i=s，可得100 -5r= - 50 +0. 2y，解得(a)的IS曲线为y=750 - 25r;同理，可得(b)的IS曲线为y=750 -50r，(c)的IS曲线为y=600 - 40r。 (2)比较(a)和(b)，可知(b)的IS曲线斜率的绝对值变小，即IS曲线平坦一些，即投资函数中的投资对利率更敏感。 (3)比较(b)和(c)，当边际消费倾向变小（从0.8变为0.75）时，IS曲线斜率的绝对值变大了，即IS曲线更陡峭一些。

  • 第2题：

    说明消费函数与储蓄函数之间的关系。
    消费函数与储蓄之间的关系可以概括为以下三个方面：
    第一，消费函数和储蓄函数之和等于总收入，即
    C（Y）＋S（Y）＝Y
    第二，平均消费倾向APC、与平均储蓄倾向APS之和恒等于1，即
    APC＋APS＝l
    第三，边际消费倾向MPC、和边际储蓄倾向MPS之和恒等于1，即
    MPC＋MPS=1
    由此可见，消费函数和储蓄函数中只要有一个确立，另一个也随之确立。
    略

  • 第3题：

    请简要说明构造函数和析构函数各自的作用。


    创建和撤销对象

  • 第4题：

    简要说明在短期中，生产函数与成本函数之间的关系


    答案：
    解析：
    (1)厂商的短期成本函数可以由成本、产量以及要素投入量之间的关系推导得出，因为一定的要素投入量生产一定产量的产品，同时也必然花费一定的成本。成本与产量之间的对应关系即为成本函数。即若给定生产函数为Q= f(L，K)，以及成本方程为C=L·PLK·PK+ CO，根据最优要素投入量的选择原则MPL/PL= MPK/PK，就可以获得短期成本函数C=C(Q)。 (2)平均可变成本AVC与给定要素价格下的可变要素数量及产量相关，因而也就与其平均产量相关；边际成本MC与给定要素价格下的边际产量相关。即：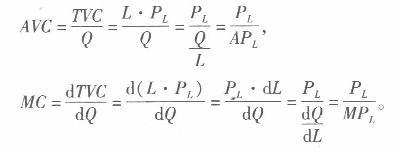

    所以，APL与4VC的变化趋势相反，APL曲线呈倒U形，AVC曲线呈U形；MPL与MC的变化趋势也相反，MP。曲线呈倒U形，MC曲线则呈U形。

  • 第5题：

    简要说明灰色关联聚类和基于可能度函数的灰色聚类评估模型


    根据序列曲线几何形状的相似程度来判断联系是否紧密

相关内容