在生命周期假设中，消费对积累的储蓄比率一直至退休时都是下降的。（1）为什么？是有关消费的什么假设导致这个结果？（2）在退休以后，这个比率如何变化？

题目

在生命周期假设中，消费对积累的储蓄比率一直至退休时都是下降的。（1）为什么？是有关消费的什么假设导致这个结果？（2）在退休以后，这个比率如何变化？

相似考题

1.根据生命周期假说，消费者的消费对积累财富的比率变化情况是（）A.在退休前，这个比率是上升的，退休后这个比率为下降；B.在退休前，这个比率是下降的，退休后则为上升；C.在退休前后，这个比率都保持不变；D.在退休前后，这个比率都下降。

2.根据生命周期假说，人们在工作期间储蓄，以便在退休是消费。()

3.人们在工作期间储蓄是为了在退休时消费的观点被称为()。A:凯恩斯的消费函数B:生命周期假说C:持久收入假说D:预期收入假说

4.依据生命周期理论，下列说法正确的有（）A.个人在一生中每年的消费水平都是大致相当的B.个人在一生中每年的收入水平都是大致相当的C.个人在一生中每年的储蓄水平都是大致相当的D.工作期间的消费支出由当前收入提供E.退休期间的消费支出由工作期间积累的储蓄实现

参考答案和解析
参考答案：

（1）根据生命周期假设，消费者每年消费C=WL(工作期限)*YL（年收入）/NL（预期寿命），则退休前每年储蓄为S=YL-C=(NL-WL)*YL/NL。至T年时积累的储蓄为WR=S*T，则消费对积累的储蓄比率为C/WR=WL/(NL-WL)*T。显然，随着T的增大，消费对积累的储蓄比例逐渐减少。这主要是由消费者将其工作收入均匀的用于其一生的消费这一假设导致的。
（2）退休后，消费者每年消费不变。而积累的储蓄为：WR=(NL-WL)*YL*WL/NL-(T-WL)*C
=(NL-T)*YL*WL/NL，其中WL≤T≤NL。则消费对积累的储蓄比例为C/WR=1/(NL-T)。显然，随着T的增大，消费对积累的储蓄比例也逐渐增大。


更多“在生命周期假设中，消费对积累的储蓄比率一直至退休时都是下降的。（1）为什么？是有关消费的什么假设 ”相关问题

  • 第1题：

    消费与储蓄的生命周期的含义是：工作期进行储蓄，退休期则使用过去的储蓄。 ( )

    此题为判断题(对，错)。


    正确答案：√

  • 第2题：

    在生命周期假设中，消费对积累的储蓄比率一直到退休时都是下降的， (1)为什么？有关消费的什么假设导致了这个结果？ (2)在退休以后，这个比率如何变化？


    答案：
    解析：
    (1)根据生命周期假设，消费者每年消费G=WL(工作期限)×YL(年收入)/NL（预期寿命），则退休前每年储蓄为S= YL -C=(NL - WL)×YUNL。至T年时积累的储蓄为WR=SxT则消费对积累的储蓄比率为C/WR= WL/（NL - WL）×T。显然，随着71的增大，消费对积累的储蓄比例逐渐减少。这主要是由消费者将其工作收入均匀地用于其一生的消费这一假设导致的。 (2)退休后，消费者每年消费不变。而积累的储蓄为WR=（NL - WL）×YL×WL/NL -（T-WL）×C=（NL -T）×YL×WL/NL，其中，WL≤T≤NL。则消费对积累的储蓄比例为C/ WR=1／(NL -T)。显然，随着T的增大，消费对积累的储蓄比例也逐渐增大。

  • 第3题：

    3、（1）假设消费者是借款者，利率上升后，如果消费者仍然是借款者，那么消费者的境况是变好还是变坏；如果消费者由借款者变成储蓄者，那么，消费者的境况是变好还是变坏？ （2）假设消费者是储蓄者，利率下降后，如果消费者仍然是储蓄者，那么消费者的境况是变好还是变坏；如果消费者由储蓄者变成借款者，那么，消费者的境况是变好还是变坏？


    如果利率上升后，消费者仍为借款者，其境况会变差;如果利率上升后，消费者变为贷款者，其境况变化取决于具体情况

  • 第4题：

    陈军打算在20年后退休，他可以在每年储蓄10000元直至退休，假设年回报率是6%，那么当他退休时收入是( )元。

    A．412523.29

    B．389927.27

    C．367855.91

    D．276513


    参考答案：C
    解析：运用财务计算器：PMT=-10000，N=20，I=6，P/YR=1，求9V7FV=367855.91。

  • 第5题：

    假设消费者生活两期，在第一期消费者劳动，获得收入，用来满足该期的消费和储蓄。消费者在第二期不劳动,用第一*期的储蓄来满足该期的消费。假设消费者在第一期的消费为c1，消费为s，劳动收入为w;在第二期的消费为c2,假设市场利率为r,贴现因子为0＜β＜1。设消费者的效用函数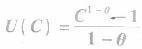

    其中，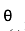

    为正常数。求： (1)写出消费者的效用极大化问题。 (2)求出消费者的储蓄函数，讨论利率的改变与储蓄的关系。 (3)将上面的结论与我国当前实际相结合，分析利率下降与储蓄的关系。


    答案：
    解析：

相关内容