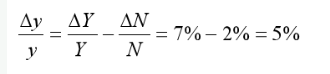计算分析题:已知资本增长率为K=2%,劳动增长率为L=0.8%,产出或收入增长率为Y=3.1%,资本的国民收入份额为a=0.25,问;技术进步对经济的贡献为多少?
题目
计算分析题:已知资本增长率为K=2%,劳动增长率为L=0.8%,产出或收入增长率为Y=3.1%,资本的国民收入份额为a=0.25,问;技术进步对经济的贡献为多少?
相似考题
更多“计算分析题:已知资本增长率为K=2%,劳动增长率为L=0.8%,产出或收入增长率为Y=3.1%,资本的国民收入 ”相关问题
-
第1题:
假定产出是根据含有失业率的生产函数Y= Kα[(l-u*)L]1-α 来表示的。在上式中,K为资本,L为劳动力,u*为自然失业率。国民储蓄率为s,劳动力增长率为n,资本折旧率为δ。 请把人均产出(y=Y/L)表示为人均资本(k=K/L)和自然失业率的函数。答案:解析:
-
第2题:
某国的生产函数为
L为劳动,K为资本,A为技术水平,储蓄率s=0.6,人口增长率n=1%,折旧率d=0. 05,技术进步率
(1)当经济实现平衡增长时,求单位效率人(AL)的资本、收入和消费水平,此时人均收入、人均资本和消费的增长率为多少?总产出和总资本增长率为多少?(2)计算单位效率人的黄金律资本水平,相应的收入、消费及储蓄率水平,说明储蓄率在该模型的作用。(3)如果生产函数变为
其他条件与(1)相同,当经济实现平衡增长时,人均收入和人均资本增长率为多少?总产出和总资本增长率为多少?答案:解析:(1)将生产函数
等式两边同除以
对具有技术进步的新古典增长模型来说,稳态条件为
以及生产函数代人到稳态条件可得:
解得:
单位效率人均收入
单位效率人均消费
当经济实现平衡增长时,人均收入、人均资本和消费的增长率都为技术进步率g,即增长率为4%。总产出和总资本增长率为人口增长率加技术进步率,为4%+1% =5%。(2)在有技术进步的稳态下,单位效率人的黄金律资本水平应满足MPK=n+d+g,即有:
解得:

给定生产函数,一旦确定了相应的储蓄率s,储蓄函数就予以确定,从而就得到稳态下的人均资本和人均产出。因此,问题在于储蓄率的确定,要求确定的储蓄率使得稳态人均消费最大化,即可以通过调整储蓄率从而实现黄金率资本水平。(3)当生产函数变为
时,当经济实现平衡增长时,人均收入和人均资本增长率为0,总产出和总资本增长率为人口增长率,即1%。 -
第3题:
已知资本增长率g1=2%,劳动增长率g,=0.8%,产出增长率g、=3.1%.资本的国民收入份额 α=0. 25,在这些条件下,技术进步对经济增长的贡献为多少?答案:解析:由题意可知,劳动的国民收入份额为6 =1一α =0. 75。 资本和劳动对经济增长的贡献为0.25 x2% +0.75 x0.8% =1.1%,所以技术进步对经济增长的贡献为3.1% -1.1% =2%。 -
第4题:
假定产出是根据含有失业率的生产函数Y= Kα[(l-u*)L]1-α 来表示的。在上式中,K为资本,L为劳动力,u*为自然失业率。国民储蓄率为s,劳动力增长率为n,资本折旧率为δ。 计算该经济的稳态的人均资本和人均产出。答案:解析:
-
第5题:
给定一国的生产函数Y=(AN)1/2K1/2,A=1,储蓄率为0.6,人口增长率为2%,折旧率为8%。
如果A=K/16N,资本的边际产出、总产出增长率和人均增长率是多少?
答案:解析:如果A=K/16N,则宏观生产函数为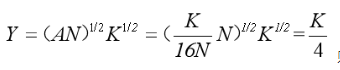
则资本的边际产出MPK=1/4,是一个常数 总产出增长率方程为: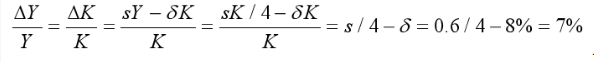
人均产出增长率为: