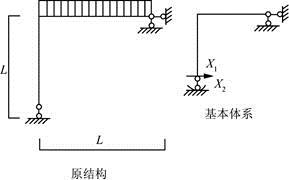
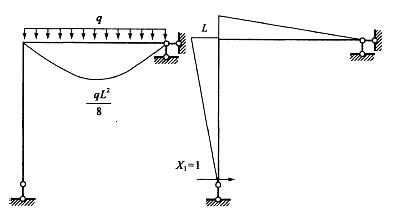
用力法求解图所示结构（EI=常数），基本体系及基本未知量如图所示，力法方程中的系数为（　　）。

题目
用力法求解图所示结构（EI=常数），基本体系及基本未知量如图所示，力法方程中的系数为（　　）。



相似考题

1.图示结构，各柱EI=常数，用位移法计算时，基本未知量数目是()A.2B.4C.6D.8

2.用力法计算，并绘图示结构的M图，EI为常数。

3.如图所示的结构，用力法求解的最少未知量数为（　　）。A、1B、2C、3D、6

4.有关力法求解超静定的结构问题,下列说法正确的是( )。A.力法的基本体系可用是瞬息变体系B.静定结构可以用力法求解C.超静定结构可以作为力法的基本体系D.结构的超静定次数不一定等于多余约束个数

更多“用力法求解图所示结构（EI=常数），基本体系及基本未知量如图所示，力法方程中的系数为（　　）。 ”相关问题

  • 第1题：

    图所示中，用力法解图（a）所示结构（图中kM为弹性铰支座A的转动刚度系数），取图（b）所示的力法基本体系，力法典型方程为（　　）。




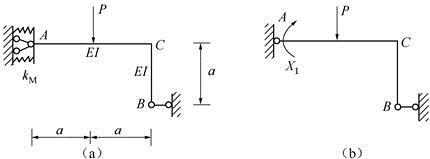
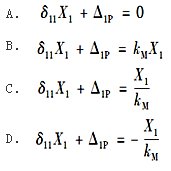    答案：D
    解析：
    该结构为一次超静定结构，建立力法典型方程得δ11X1+Δ1P=Δ1，力法典型方程是变形协调方程，因此方程右端的Δ1表示原超静定结构沿X1方向的给定位移。在图（b）所示力法基本体系中，Δ1表示截面A的转角，

  • 第2题：

    用力法求解图示结构(EI=常数），基本体系及基本未知量如图所示，力法方程中系数△1P为：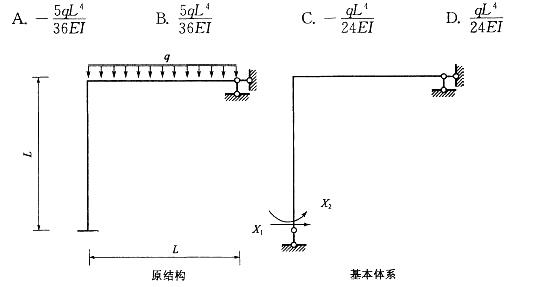


    答案：C
    解析：

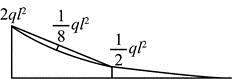
  • 第3题：

    如图a)所示结构，EI=常数，取图b)为力法基本体系，则下述结果中错误的是:


    A.δ23=0
    B. δ31=0
    C.Δ2P=0
    D.δ12=0

    答案：D
    解析：
    提示：根据图乘法或物理概念判断。

  • 第4题：

    如图所示，用力法且采用图（b）所示的基本体系计算图（a）所示梁，Δ1P为（　　）。




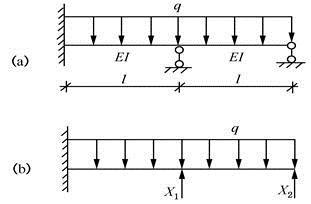
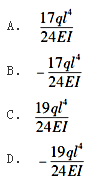    答案：D
    解析：
    作出在基本体系下荷载的弯矩图，以及在基本结构体X1为单位力时的弯矩图。如图所示。则将要计算部分化成标准抛物线及三角形，正方形后，计算Δ1P，则


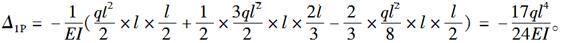
  • 第5题：

    图示结构取图（b）为力法基本体系，EI为常数，下列哪项是错误的？（　　）


    答案：D
    解析：

  • 第6题：

    用位移法求解图所示结构，独立的基本未知量个数为（　　）。


    A、1
    B、2
    C、3
    D、4

    答案：A
    解析：
    若不考虑杆件的轴向变形，则结构存在一个独立的位移分量即中间刚节点的转角位移。若考虑杆件的轴向变形，则结构存在三个独立的位移分量：①左端节点的水平位移；②中间节点的竖向位移；③中间刚节点处的转角位移。位移法求解时，通常不考虑杆件轴向变形。

  • 第7题：

    图所示结构取图（b）为力法基本体系，El为常数，下列哪项是错误的[A8] ?（　　）




    答案：D
    解析：

  • 第8题：

    图中，用力法求解图（a）所示结构，取图（b）所示力法基本体系，则力法典型方程δ11X1+Δ1p=0中的Δ1P之值为（　　）。




    答案：D
    解析：

  • 第9题：

    如图所示的结构，EI＝常数，用力矩分配法计算时，分配系数μA1为（　　）。


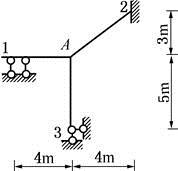    A、1/8
    B、1/3
    C、4/11
    D、5/12

    答案：D
    解析：
    当结点A转动时，A1杆的1端既无角位移也无线位移，其约束性能相当于固定支座，2处为固定支座，3处为铰支座。所以分配系数

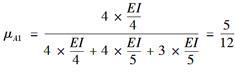
  • 第10题：

    如图a)所示结构，取图b)为力法基本体系，EI=常数，Δ1P为:



    答案：C
    解析：
    提示:应用图乘法。

  • 第11题：

    图a)所示桁架，EA=常数，取图b)为力法基本体系，则力法方程系数间的关系为：

    A. δ2211,δ12>0 B.δ22>δ11,δ12>0
    C. δ2211,δ1222>δ11,δ12


    答案：B
    解析：
    提示:利用杆的拉压性质判断副系数，通过计算判断主系数。

  • 第12题：

    力法求解超静定结构的第一步为（）。

    • A、列出力法方程
    • B、内力图校核
    • C、求解基本未知量
    • D、确定结构的超静定次数，选取基本未知量并确定基本体系。

    正确答案:D

  • 第13题：

    如图a)所示结构，若将链杆撤去，取图b)为力法基本体系，则力法方程及知分别为:



    答案：C
    解析：
    提示：力法方程等号右端应为负，并计算δ11。

  • 第14题：

    用力法计算图（a）所示结构，取基本结构如图（b）所示，其中系数δ11为（　　）。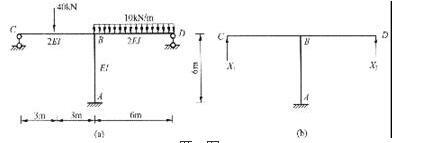



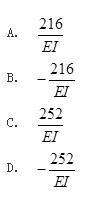    答案：C
    解析：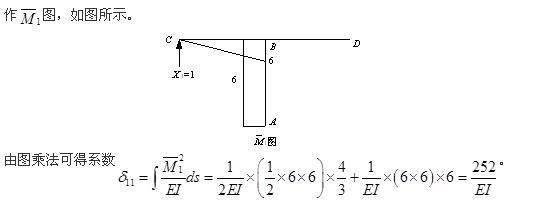

  • 第15题：

    如图a所示桁架，EA为常数，取图b为力法基本体系，则力法方程系数间的关系为（　　）。


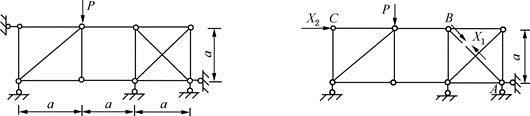    A、δ22＜δ11，δ12＞0
    B、δ22＞δ11，δ12＞0
    C、δ22＜δ11，δ12＜0
    D、δ22＞δ11，δ12＜0

    答案：B
    解析：
    解法一：利用结构力学基本概念求解。对X1、X2的作用位置进行分析可知，X2作用点的水平侧移刚度较弱（左侧、右侧两个正方形刚片串联），故δ22>δ11；同时当X2作用点发生向右的水平侧移时，X1方向上两铰接点间的距离变小，即δ12>0。
    解法二：根据图示静定基本机构作出N1图和N2图，如图所示。



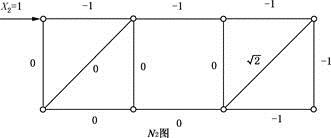
    则可得：

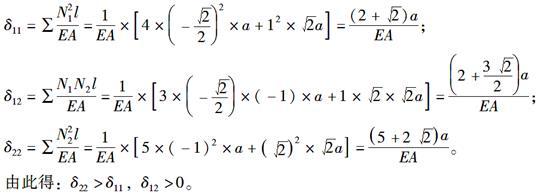
  • 第16题：

    如图所示的位移法基本体系中（图中结点B处的竖向刚性支杆为基本体系中的附加支杆），基本结构的刚度系数k11之值为（　　）。




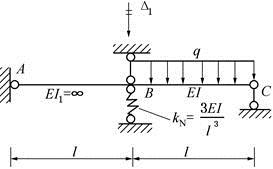
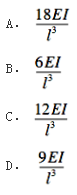    答案：D
    解析：

  • 第17题：

    如图（a）所示的结构，EI＝常数，取图（b）为力法基本体系，则下列各项错误的是（　　）。


    A、δ23＝0
    B、δ31＝0
    C、Δ2P＝0
    D、δ12＝0

    答案：D
    解析：



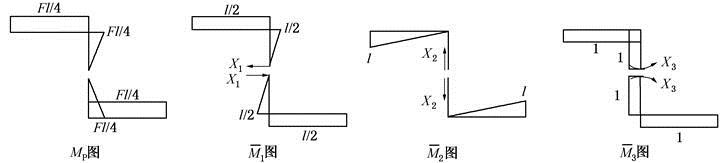
    根据弯矩图的对称性得，δ13=δ23=Δ1P=Δ2P=0。

  • 第18题：

    如图a)所示桁架，EA=常数，取图b)为力法基本体系，则力法方程系数间的关系为：


    A. δ2211,δ12>0 B.δ22>δ11,δ12>0
    C. δ2211,δ1222>δ11,δ12

    答案：B
    解析：
    提示：利用杆的拉压性质判断副系数，通过计算判断主系数。

  • 第19题：

    图a)所示结构，取图b)为力法基本体系，则力法方程中的Δ2C为: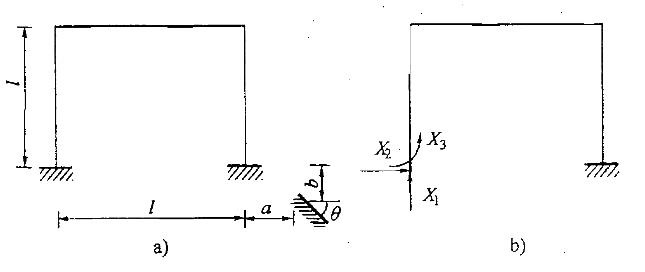


    A. a+b
    B. a+lθ
    C. -a
    D. a

    答案：D
    解析：
    提示：用公式求，或根据几何关系分析。

  • 第20题：

    用位移法计算图所示梁（EI=常数），基本体系如图所示，k11为（　　）。

    A、6EI/l
    B、7EI/l
    C、8EI/l
    D、9EI/l

    答案：B
    解析：
    当Z1为单位转角时，左端产生的弯矩为顺时针向的3i，右端产生的弯矩也为顺时针，值为4i，则k11=3i+4i=7i，i=EI/l，所以k11=7EI/l。

  • 第21题：

    图a)所示桁架，EA=常数，取图b)为力法基本体系，则力法方程系数间的关系为:

    A.δ11=δ22,δ12>0 C.δ11≠δ22,δ12>0B.δ11≠δ22,δ1211=δ22,δ12


    答案：B
    解析：
    提示:利用杆的拉压性质判断副系数，通过计算判断主系数。

  • 第22题：

    如图a)所示结构，取图b)为力法基本体系，则力法方程中的Δ2C为: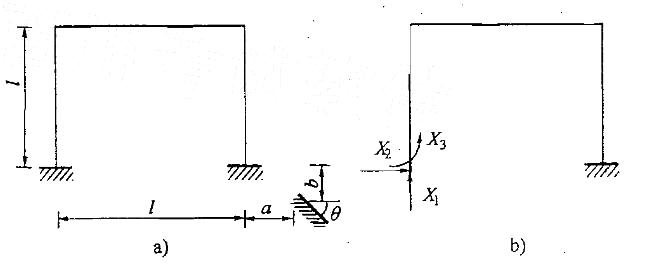

    A. a+b B. a+lθ C. -a D. a


    答案：D
    解析：
    提示:用公式求，或根据几何关系分析。

  • 第23题：

    用力法求解图示结构时，基本未知量的个数是（）。

    A5

    B6

    C7

    D8


    B
    略

相关内容