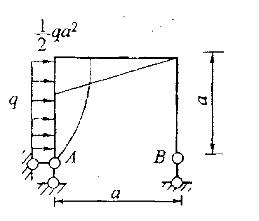
图示为刚架在均布荷载作用下的M图，曲线为二次抛物线，横梁的抗弯刚度为2EI，竖柱为EI，支座A处截面转角为：

题目
图示为刚架在均布荷载作用下的M图，曲线为二次抛物线，横梁的抗弯刚度为2EI，竖柱为EI，支座A处截面转角为：


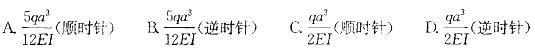
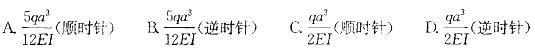
相似考题

1.图示结构EI=常数，截面A右侧的弯矩为()A.M/2B.MC.0D.M/(2EI)

2.绘制平面刚架弯矩图时,受均布荷载作用,弯矩图的形状为()。A、抛物线B、折线C、直线D、曲线

3.图示两端铰支压杆的截面为矩形，当其失稳时： A.临界压力Pcr=π2EI∥ι^2，挠曲线位于xy面内 B.临界压力Pcr=π2EI∥ι^2，挠曲线位于xy面内 C.临界压力Pcr=π2EI∥ι^2，挠曲线位于xy面内 D.临界压力Pcr=π2EI∥ι^2，挠曲线位于xz面内

4.在反弯点法中,假定梁的刚度为无限大,框架在水平荷载作用下只有(),节点()转角。

参考答案和解析
答案：A
解析：
提示：应用图乘法。
更多“图示为刚架在均布荷载作用下的M图，曲线为二次抛物线，横梁的抗弯刚度为2EI，竖柱为EI，支座A处截面转角为：”相关问题

  • 第1题：

    在图示体系中，集中质量为m，杆长为l，抗弯刚度为EI，杆重不计。该体系自由振动的周期为（　　）。



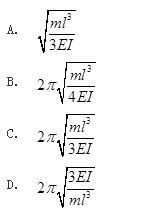    答案：C
    解析：

  • 第2题：

    图示结构，当支座B发生沉降Δ时，支座B处梁截面的转角大小为: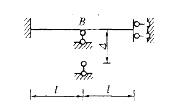



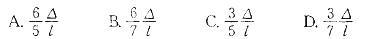    答案：A
    解析：
    提示：建立结点B的平衡方程。

  • 第3题：

    结构在荷载下的弯矩图如图所示，曲线为q＝2kN／m引起的二次抛物线，EI＝常数。B点的水平位移为（　　）。

    A．108／（EI）（→）
    B．756／（EI）（→）
    C．828／（EI）（→）
    D．900／（EI）（→）

    答案：D
    解析：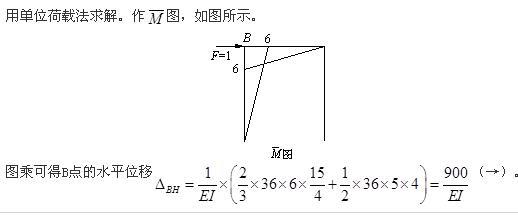

  • 第4题：

    图示连续梁，EI=常数，已知支承B处梁截面转角为-7Pl2/240EI（逆时针向），则支承C处梁截面转角φC应为：



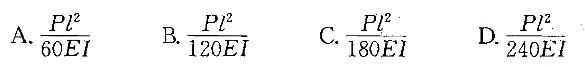    答案：B
    解析：
    提示：由结点C的平衡求解。

  • 第5题：

    若要保证图所示结构在外荷载作用下，梁跨中截面产生负弯矩可采用（　　）。


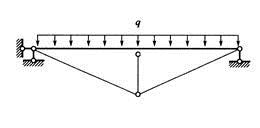    A、增大二力杆刚度且减小横梁刚度
    B、减小二力杆刚度且增大横梁刚度
    C、减小均布荷载q
    D、该结构为静定结构，与构件刚度无关

    答案：A
    解析：
    要使梁跨中截面产生负弯矩，即梁跨中要向上弯曲。材料刚度是指材料在受力时抵抗弹性变形的能力，若竖向杆（二力杆）的刚度很小，就无法抵抗梁因均布荷载作用而产生的向下的变形；若竖向杆的刚度很大，梁跨中处几乎就不能产生向下的变形，而跨中两侧梁产生向下的变形，此时，在梁跨中处就会产生负弯矩。若横梁刚度较大，梁的变形能力就差，在均布荷载作用下，几乎不会产生变形，也就不会产生负弯矩。

  • 第6题：

    若要保证图示结构在外荷载作用下，梁跨中截面产生负弯矩（上侧纤维受拉），可采用（　　）。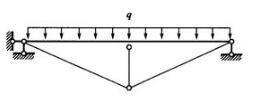

    A、增大二力杆刚度且减小横梁刚度
    B、减小二力杆刚度且增大横梁刚度
    C、减小均布荷载q
    D、该结构为静定结构，与构件刚度无关

    答案：A
    解析：
    超静定结构内部杆件受力与相对刚度有关，刚度越大的杆件分担的内力也越大，因此，应增大二力杆的刚度来改变横梁的受力状态，二力杆刚度越大，竖杆对横梁的支撑作用越大，使得横梁跨中产生负弯矩。

  • 第7题：

    图示梁的抗弯刚度为EI，长度为l，欲使梁中点C弯矩为零，则弹性支座刚度k的取值应为（　　）




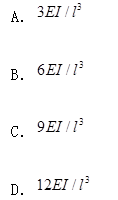    答案：B
    解析：
    知识点:利用力法对超静定结构的内力求解；

  • 第8题：

    图示结构EI=常数，当支座B发生沉降Δ时，支座B处梁截面的转角为（以顺时针为正）（　　）。


    A、Δ/l
    B、1、2Δ/l
    C、1、5Δ/l
    D、Δ/2l

    答案：B
    解析：

  • 第9题：

    图示为结构在荷载作用下的M图，各杆EI=常数，则支座B处截面的转角为: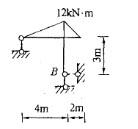



    答案：A
    解析：
    提示:应用图乘法。

  • 第10题：

    已知图示梁抗弯刚度EI为常数，则用叠加法可得自由端C点的挠度为：



    答案：D
    解析：
    提示：为了查表方便，先求整个梁布满向下均布荷载时C点的挠度，再减去AB段承受向上均布荷载时C点的挠度。

  • 第11题：

    框架柱在水平荷载作用下的标准反弯点，是依据规则框架求得的柱反弯点，所谓规则框架是指框架满足条件（）。

    • A、各层等高
    • B、各跨相等
    • C、各节点转角为零
    • D、各层梁柱线刚度不变
    • E、受均布荷载作用

    正确答案:A,B,C,D

  • 第12题：

    判断题
    在竖向均布荷载作用下，拱的合理拱轴线为二次抛物线。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第13题：

    若要保证图示结构在外荷载作用下，梁跨中截面产生负弯矩(上侧受拉) 可釆用：

    A.增大二力杆刚度且减小横梁刚度
    B.减小二力杆刚度且增大横梁刚度
    C. 减小均布荷载
    D. 该结构为静定结构，与构件刚度无关


    答案：A
    解析：
    提示：增大下部二力杆的刚度可减小梁的挠度和弯矩，有可能使梁产生负弯矩。

  • 第14题：

    已知刚架的弯矩图如图所示，杆的抗弯刚度为杆的为2EI，则结点B的角位移等于：




    答案：C
    解析：
    提示：使用BA杆的转角位移方程。

  • 第15题：

    图示结构EI＝常数，当支座A发生转角θ支座B处截面的转角为（以顺时针为正）（　　）。

    A．θ/3
    B．2θ/5
    C．－θ/3
    D．－2θ/5

    答案：D
    解析：
    在截面B处施加一个刚臂，根据位移法形常数公式，MBA＝4iθB＋2iθA－6iΔ/l＝4iθB＋2iθ，MBC＝iθB。根据结点B受力平衡，∑MB＝MBA＋MBC＝4iθB＋2iθ＋iθB＝0，解得：θB＝－2θ/5。

  • 第16题：

    图示梁AB，EI为常数，固支端A发生顺时针的支座转动，由此引起的B处的转角为（　　）。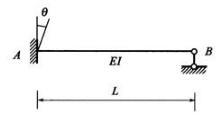



    答案：D
    解析：

  • 第17题：

    图示刚架，EI为常数，忽略轴向变形。当D支座发生支座沉降时，B点转角为（　　）。




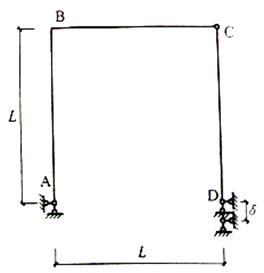
    答案：A
    解析：
    运用单位荷载法，在B点作用一个顺时针方向的单位力矩，求得D点的支座反力为

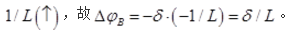
  • 第18题：

    图示梁的抗弯刚度为EI，长度为l，k＝6EI/l3，跨中C截面弯矩为（以下侧受拉为正）（　　）。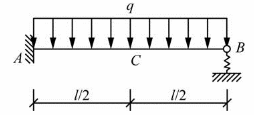

    A．0
    B．ql2/32
    C．ql2/48
    D．ql2/64

    答案：A
    解析：
    撤去支座B约束，代以未知反力X，方向向上，得到力法的基本体系，则有力法方程δ11X1＋Δ1P＝－X1/k。作出均布荷载单独作用下基本体系的弯矩图，如题42解图（a）所示。在B端作用一个方向向上的单位力，并做出弯矩图，如题42解图（b）所示。由图乘法：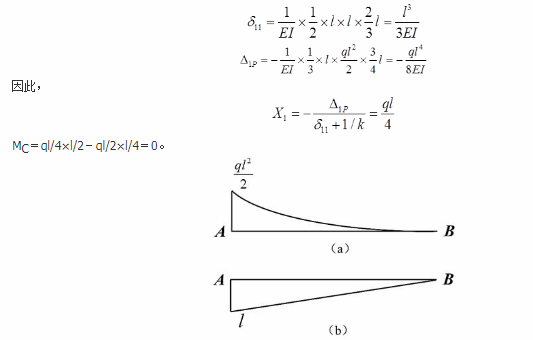

  • 第19题：

    图示结构B截面转角位移为（以顺时针为正）（　　）。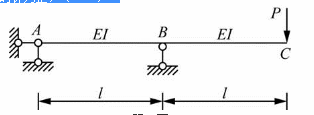

    A．Pl2/（EI）
    B．Pl2/（2EI）
    C．Pl2/（3EI）
    D．Pl2/（4EI）

    答案：C
    解析：
    方法一：竖向力P在B点作用的弯矩为Pl，根据简单荷载作用下梁的挠度和转角公式，θB＝MBl/（3EI），代入得，θB＝Pl2/（3EI）。方法二：采用单位荷载法结合图乘法计算。在截面B处施加一个单位力偶，分别作出单位力偶和外荷载作用下的弯矩图，如题40解图所示。由图乘法，

  • 第20题：

    图示结构当水平支杆产生单位位移时（未注的杆件抗弯刚度为EI），B-B截面的弯矩值为（　　）。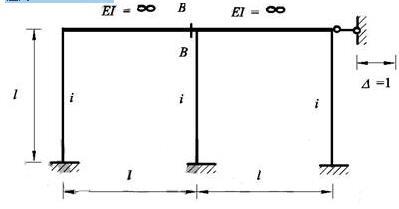



    答案：C
    解析：
    由题39图可知，在计算B-B截面的弯矩时，先把B点看成一个固定端。则可把B到最右端看成是一个一端铰接一端固定的直杆。再根据表1可得B端的弯矩为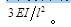

    表1　等截面直杆的固端弯矩和固端剪力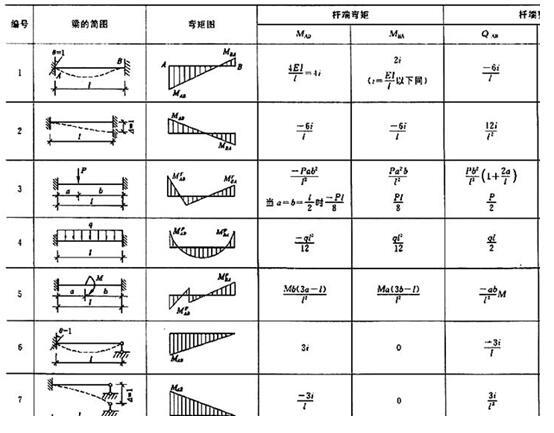

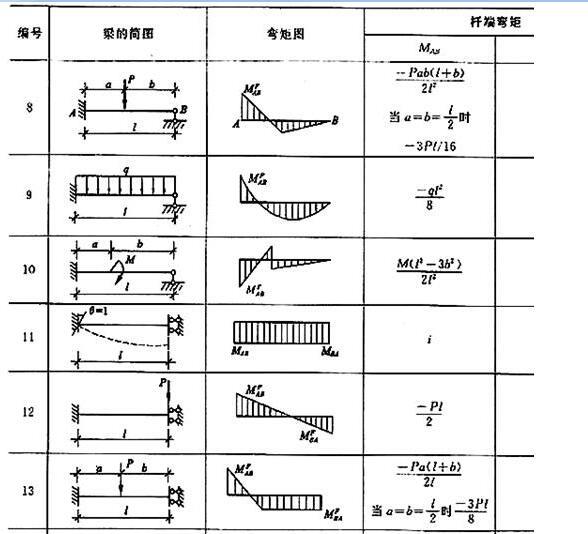
  • 第21题：

    已知图示梁抗弯刚度EI为常数，则用叠加法可得跨中点C的挠度为：



    答案：C
    解析：
    提示：图示梁荷载为均布荷载q的一半，中点挠度也是均布荷载简支梁的一半。

  • 第22题：

    若拱轴线为二次抛物线，则在均布荷载作用下，拱肋截面内只有轴力，弯矩和剪力为零。


    正确答案:正确

  • 第23题：

    在竖向均布荷载作用下，拱的合理拱轴线为二次抛物线。


    正确答案:正确

相关内容