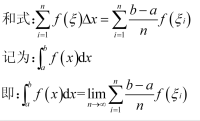请教:2011年成人高考《高等数学一》预测试卷(1)第1大题第4小题如何解答?【题目描述】第 4 题
题目
【题目描述】
第 4 题


相似考题
更多“请教:2011年成人高考《高等数学一》预测试卷(1)第1大题第4小题如何解答? 【题目描述】 第 4 题”相关问题
-
第1题:
请教:2010年成人高考专升本《高等数学二》全真模拟试卷(1)第1大题第1小题如何解答?【题目描述】
第 1 题
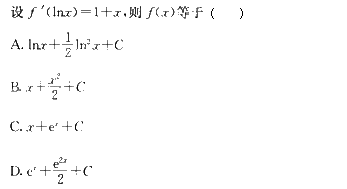
正确答案:C
解:令X=lnx,则x=ex
所以f′(X)=1+ ex
两边同时积分得f(X)=X+ ex+C
所以f(x)=x+ ex+C
这就是替代还原的方法
-
第2题:
请教:2010年教师公开招聘《小学数学》专家命题预测试卷(1)第7大题第1小题如何解答?【题目描述】
第 23 题

【参考答案分析】:
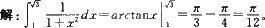
这个题目所求是一般的定积分,设函数f(x) 在区间[a,b]上连续,将区间[a,b]分成n个子区间[a,x0],(x0,x1], (x1,x2],…,(xi,b].在每个子区间(xi-1,xi)任取一点ξi(i=1,2,…,n),作和式(见右下图),当λ→0时,(λ属于最大的区间长度)该和式无限接近于某个常数,这个常数叫做函数f(x) 在区间(a,b)的定积分,记为(见右下图):
其中:a叫做积分下限,b叫做积分上限,区间【a,b】叫做积分区间,函数f(x) 叫做被积函数,x 叫做积分变量,f(x)dx 叫做被积式,∫ 叫做积分号。之所以称其为定积分,是因为它积分后得出的值是确定的,是一个数, 而不是一个函数。
-
第3题:
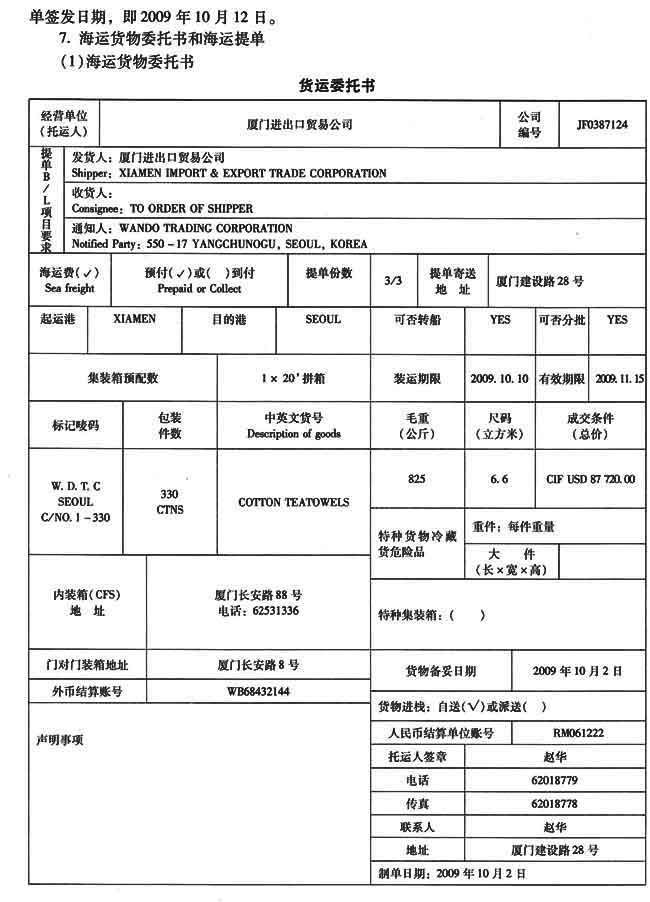
请教:2010单证员缮制与操作单据缮制预测(4)第1大题第1小题如何解答?【题目描述】
第1题:
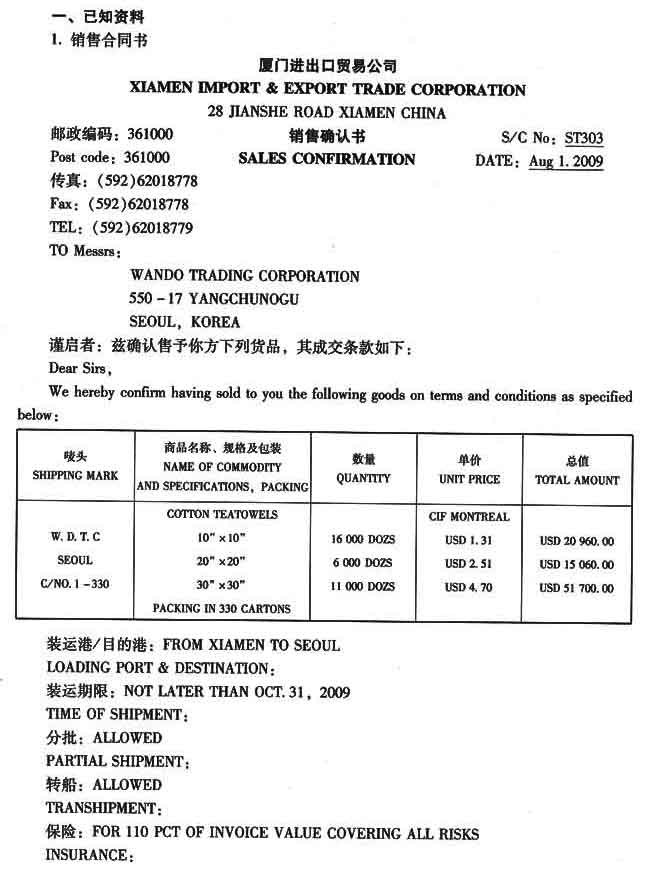






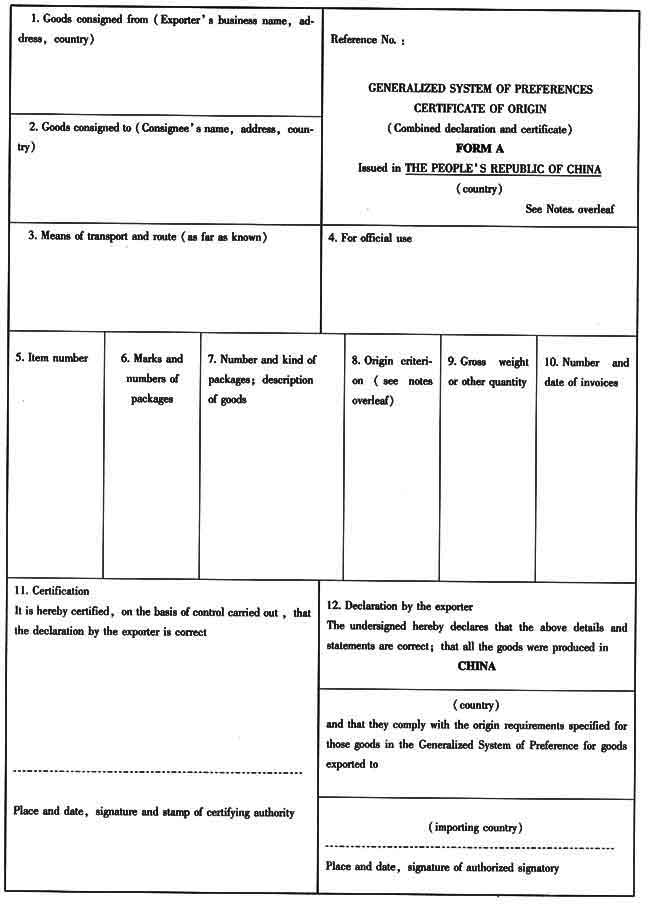
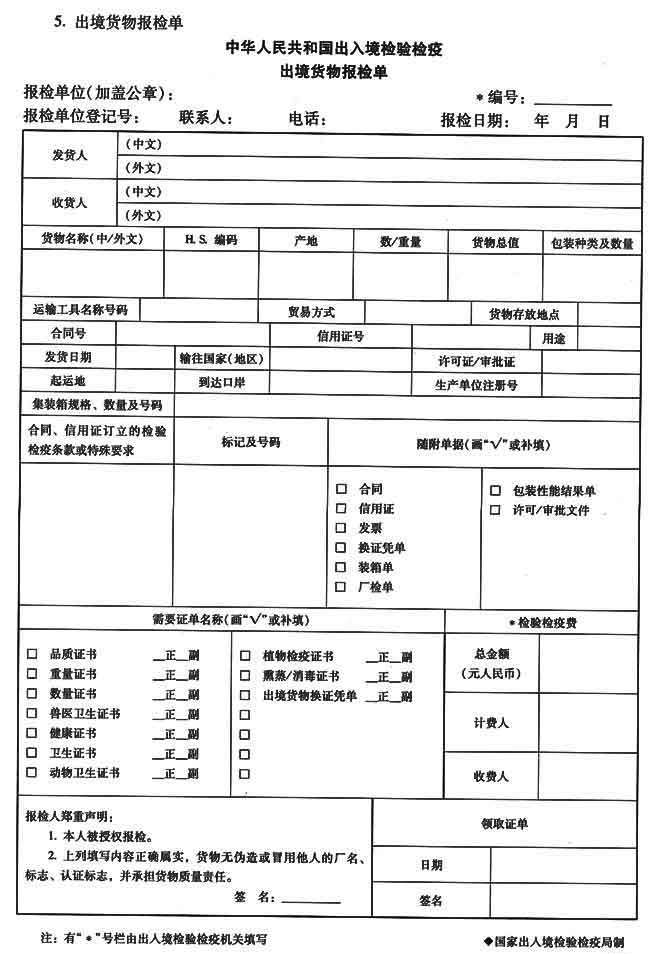


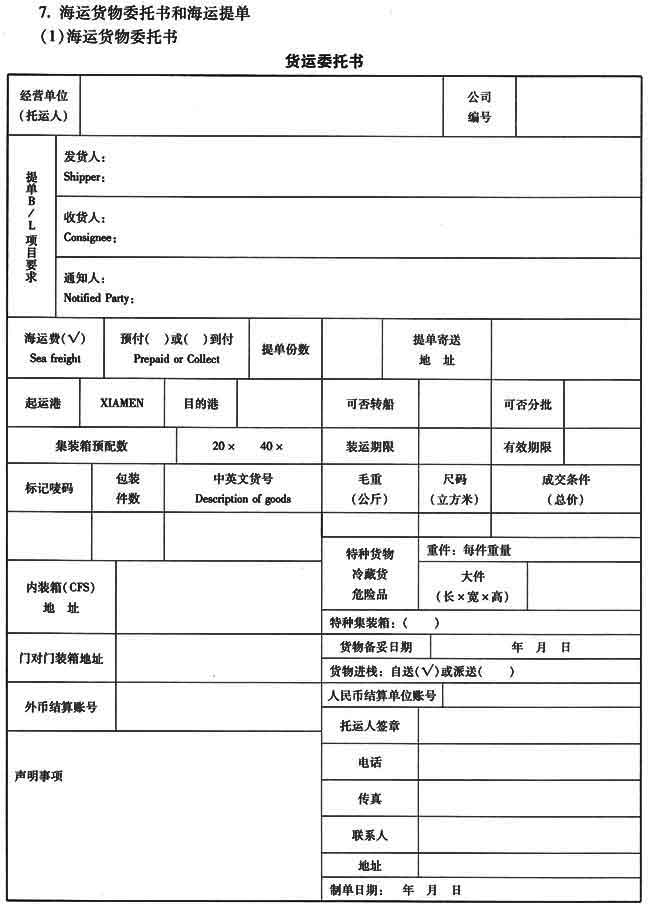
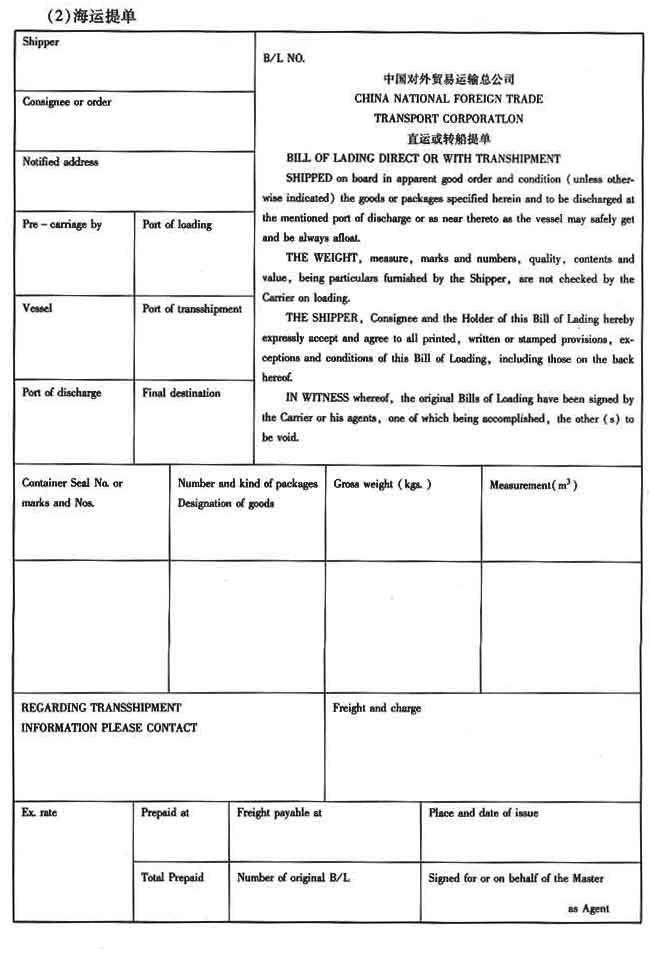
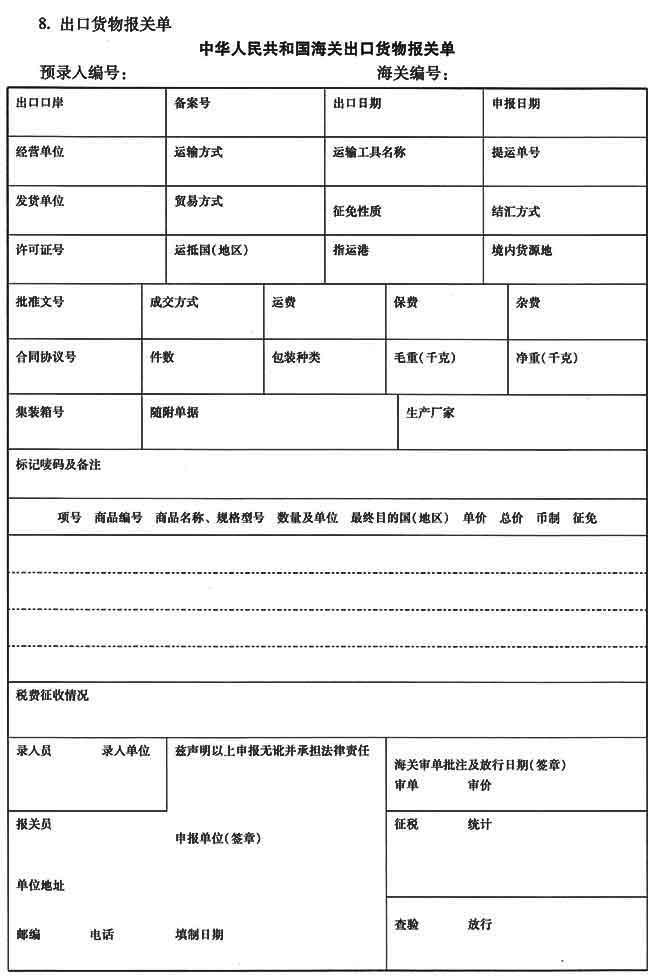 【参考答案分析】:
【参考答案分析】: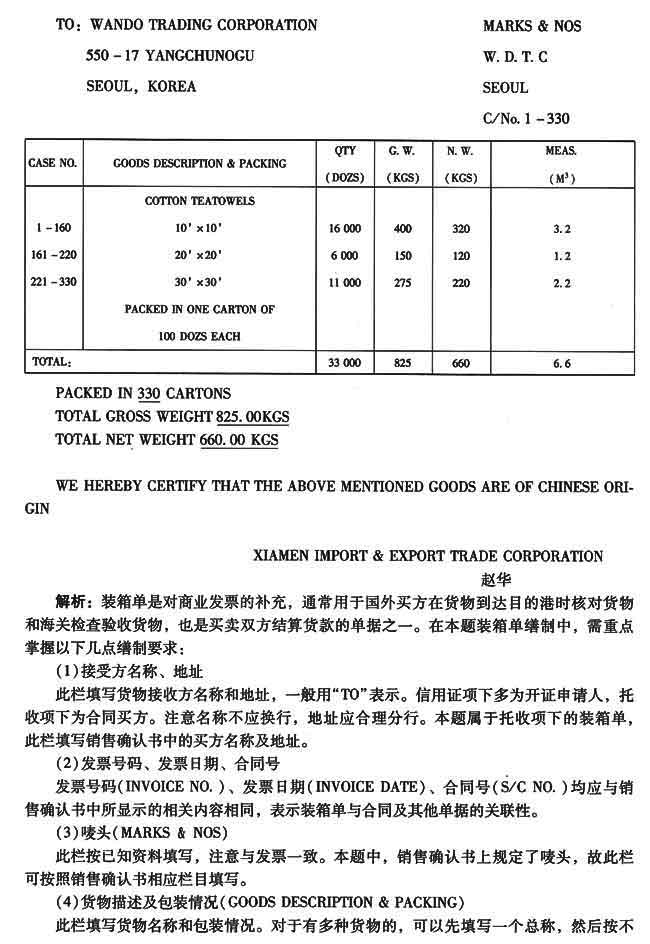

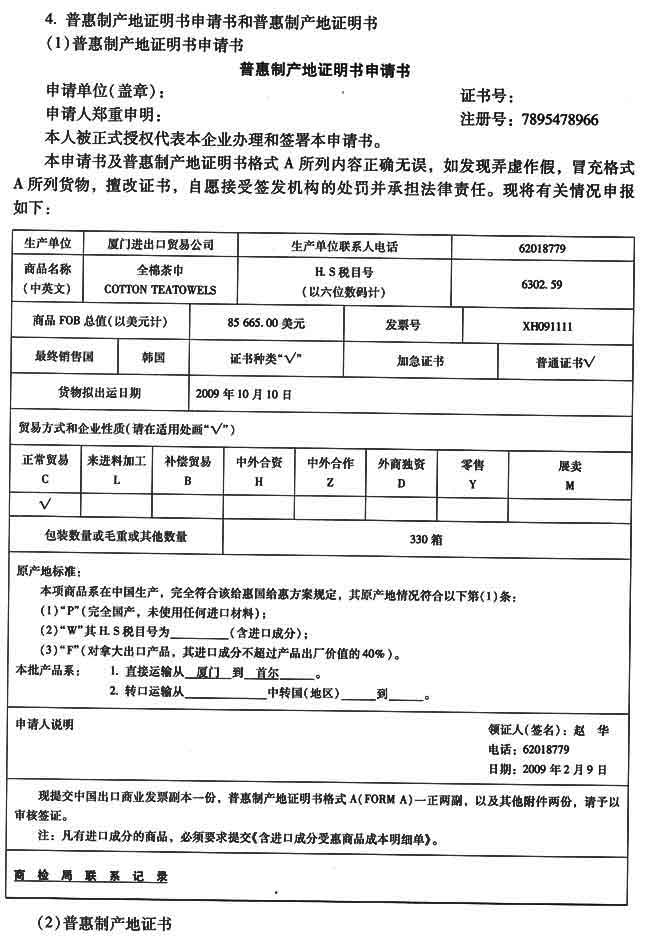
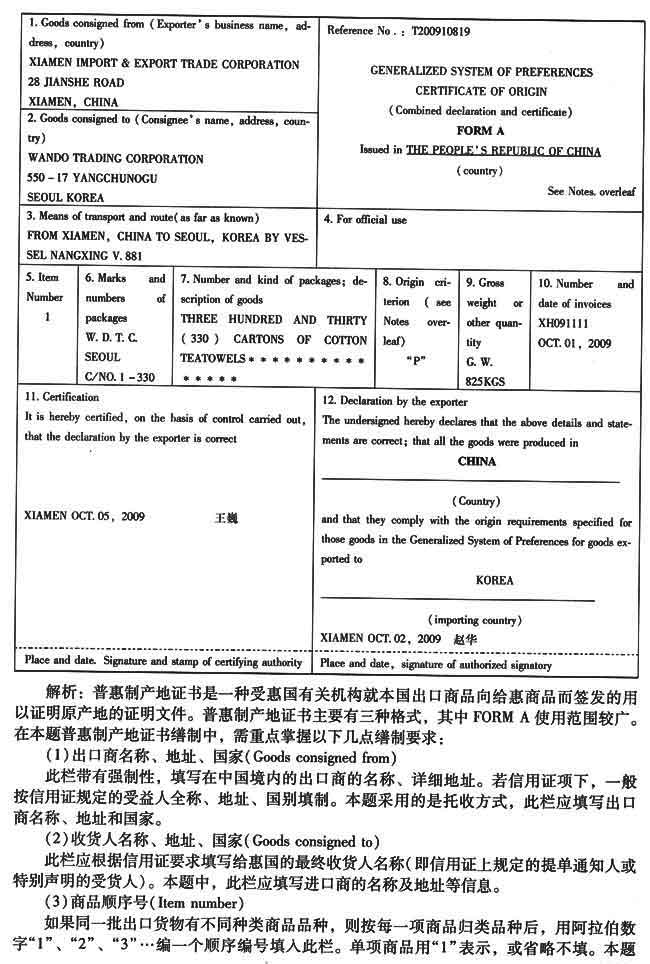





-
第4题:
请教:2011年会计从业考试《初级会计电算化》命题预测试卷(1)第4大题第1小题如何解答?【题目描述】
第 86 题

【参考答案分析】:
答案暂无。
可使用“资源管理器”窗口或“我的电脑”窗口进行文件或文件夹的新建、复制、移动、删除、重命名(更名)、创建快捷方式等操作。
可以通过三种方式进行操作,即选择菜单栏的菜单项、单击鼠标右键弹出快捷菜单、鼠标(左键或右键)拖曳。
使用“资源管理器”窗口可左、右窗格之间进行操作。使用“我的电脑”窗口,则要在依次弹出的多个窗口之间进行操作,需要同时打开多个“我的电脑”窗口。
Windows98的操作特点是:先选定对象,再进行操作。因此,要熟练掌握选定对象的方法。
(1)、双击我的电脑,打开D盘,在根目录下建立新文件夹:右击—新建—文件夹,重名为为NL,然后双击打开新建的文件夹NL,在里面新建两个新文件夹,重复上面的操作,然后分别重命名为N11和N12。
(2)、双击打开N11文件夹,新建一个空白文本文档,右击—新建—文本文档,重名为LIANXI.tex。(3)、将新建的文本文件选中,然后右击,在出现的下拉菜单中选择复制,然后后退到上一层,双击文件夹N12打开,在空白处右击,选择粘贴即可。
(4)、将复制过来的名为LIANXI.tex选中,然后右击,在下拉菜单中选择重命名,更改为EXEC.txt,然后回车即可。
(5)、打开N11文件夹,选中里面的名为LIANXI.tex文件夹,然后右击,在下拉菜单中选择删除,接着在桌面上找到回收站,双击回收站,找到刚删除的LIANXI.tex文件夹,然后选中并右击,点击还原按钮即可。(6)、打开N12文件夹,找到名为EXOT3.txt,选中此文件夹,然后右击—属性,在常规选项中的属性选择为隐藏,在隐藏前面的小方框里点击打钩,然后按下确定即可。
-
第5题:
请教:2011年成人高考高起点《数学(文史财经类)》预测试卷(2)第2大题第1小题如何解答?【题目描述】
第 18 题
 【参考答案分析】:(0,2)利用抛物线,把提取x平方出来,
【参考答案分析】:(0,2)利用抛物线,把提取x平方出来,2(x-3)-11,
-
第6题:
请教:2011年全国计算机等级考试二级VB全真模拟试卷(4)第1大题第4小题如何解答?【题目描述】
第 4 题

 正确答案:C
正确答案:C -
第7题:
请教:2011年成人高考高起点《语文》模拟预测试卷1第7大题第1小题如何解答?【题目描述】
第 22 题

【参考答案分析】:
略
-
第8题:
请教:2010年成人高考专升本高等数学(一)真题第1大题第1小题如何解答?【题目描述】
第 1 题
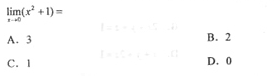
正确答案:C
-
第9题:
请教:2011年成人高考《高等数学一》预测试卷(9)第1大题第2小题如何解答?【题目描述】
第 2 题

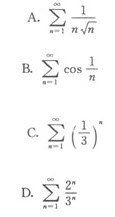 正确答案:B
正确答案:B -
第10题:
请教:2011年成人高考高起点《数学(文史财经类)》预测试卷(2)第1大题第4小题如何解答?【题目描述】
第 4 题

正确答案:C
解析:本题首先要判断函数的增减性。
1、令f(x)=x+1/x
2、令0<x1<x2<无穷大
3、那么,f(x2)-(f(x1)=(x2-x1)+(1/x2-1/x1)
=[(x2-x1)*(x1x2+1)]/x1x2 (通分得到)
>0
即:f(x2)>(f(x1)
所以0<x1<x2<无穷大时,f(x)=x+1/x为增函数。
故:f(x)在x属于[[2,5]时,值域[5/2,26/5]。所以选C
题目就是求函数y=x+1/x在区间【2,5】上的值域,由于x>1时y=x+1/x是增函数(用定义或导数都可以证明),所以有所给的结果您好!
y=x+1/x【典型的双钩函数】
x∈[2,5],因为y=x+1/x2√[x*(1/x)]=2
当且仅当x=1/x,即x=1时取的最小值【不过这里我们取不到】
它在[2,5]上单调递增
所以最小值是f(2)=2+1/2=5/2,最大值是f(5)=5+1/5=26/5
所以值域是[5/2,26/5]
祝学习愉快! -
第11题:
请教:2010年成人高考专升本高等数学(一)真题第1大题第7小题如何解答?【题目描述】
第 7 题
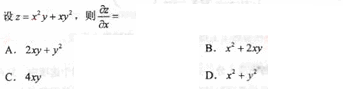
正确答案:A
-
第12题:
请教:2011年成人高考《高等数学一》预测试卷(1)第1大题第3小题如何解答?【题目描述】
第 3 题

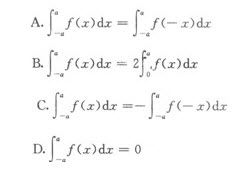
正确答案:A
-
第13题:
请教:2012年成人高考《数学(文史财经类)》预测试卷(二)第1大题第1小题如何解答?【题目描述】
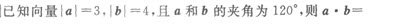

正确答案:D
-
第14题:
请教:2010年成人高考高起点《语文》全真模拟试题(4)第1大题第3小题如何解答?【题目描述】
第 3 题
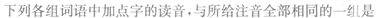 ( )
( )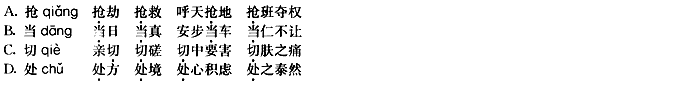
正确答案:D
-
第15题:
请教:2010年成人高考高起点《数学(文科)》命题预测试题(9)第1大题第1小题如何解答?【题目描述】
第 1 题
 正确答案:A
正确答案:A -
第16题:
请教:2010年成人高考专升本《高等数学一》全真模拟试卷(9)第1大题第5小题如何解答?【题目描述】
第 5 题
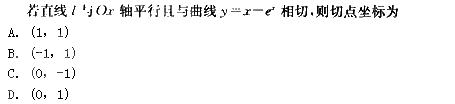
正确答案:C
-
第17题:
请教:2011年深圳市会计从业《初级会计电算化》标准预测试卷(4)第3大题第1小题如何解答?【题目描述】
第 91 题

【解析】略
-
第18题:
请教:2010年成人高考专升本数学(一)预测题(2)第1大题第3小题如何解答?【题目描述】
第3题:
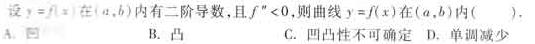
正确答案:A
答案分析:

-
第19题:
请教:2011年成人高考高起点《数学(理工农医类)》预测试卷7第1大题第2小题如何解答?【题目描述】
第 2 题
 正确答案:B
正确答案:B -
第20题:
请教:2011年成人高考高起点《数学(理工农医类)》预测试卷1第1大题第2小题如何解答?【题目描述】
第 2 题
 正确答案:D
正确答案:D -
第21题:
请教:2011年成人高考高起点《数学(文史财经类)》预测试卷(10)第1大题第1小题如何解答?【题目描述】
第 1 题
 正确答案:A
正确答案:A -
第22题:
请教:2011年成人高考高起点《数学(文史财经类)》预测试卷(4)第1大题第1小题如何解答?【题目描述】
第 1 题
 正确答案:C解析:
正确答案:C解析:
1、这是一个排列的问题。首先考虑个位,个位必须为偶数有3个选择,然后十位还剩4个数,所以十位有4个选择,依次论推百位有3个选择,千位有两个,所以为2×3×4×3=72,
2、扣除千位是0的,既把千位确定为0,然后选择,个十百位选择依次为2×3×2=12,所以最终答案应该为72-12=60。
3、所以选C -
第23题:
请教:2003年程序员上午试卷第1大题第4小题如何解答?【题目描述】

正确答案:A