给出数学文化的内容,请举出数学课堂中两个能够应用数学文化的例子.?
题目
给出数学文化的内容,请举出数学课堂中两个能够应用数学文化的例子.?
相似考题
更多“给出数学文化的内容,请举出数学课堂中两个能够应用数学文化的例子.?”相关问题
-
第1题:
数学的产生与发展过程蕴含着丰富的数学文化。
(1)以“勾股定理”教学为例,说明在数学教学中如何渗透数学文化。
(2)阐述数学文化对学生数学学习的作用。
答案:解析:本题考查数学文化在数学教学过程中的渗透。数学文化包含数学思想、数学思维方式和数学相关历史材料等方面。 -
第2题:
数学的产生与发展过程中蕴含着丰富的数学文化。
(1)以“导数及其应用”数学为例,说明数学教学中如何渗透数学文化;
(2)阐述数学文化对学生数学学习的作用。答案:解析:本题考查数学文化。数学文化包含数学思想、数学思维方式和数学相关历史材料等方面。 -
第3题:
《普通高中数学课程标准(实验)》将“( )、数学建模、数学文化”作为贯穿整个高中数学课程的重要学习活动,渗透或安排在每个模块或专题中,正是与创新能力培养的一个呼应,强调如何引导学生去发现问题、提出问题。A、数学探究
B、数学应用
C、数学思想
D、数学概念答案:A解析: -
第4题:
数学的产生与发展过程蕴含着丰富的数学文化。
(1)以“导数及其应用”教学为例,说明在数学教学中如何渗透数学文化;
(2)阐述数学文化对学生数学学习的作用。答案:解析:(1)①数学史知识的渗透 学生在学习高中数学导数知识的时候,不同于在小学就有所接触的方程等知识,导数是一个全新的概念。
因此,学生对于导数的历史比较感兴趣,教师可以利用这一点,对学生进行数学史知识的渗透,告诉学生导数的由来、发展和在实际生活、工作中的作用。这样就可以调动学生积极性,撇去导数的枯燥乏味,使之变为活泛、有趣。
②数学思想方法的渗透
a.极限思想。导数及其应用这部分知识主要从函数的连续性,导数的概念,导数的计算等方面渗透极限思想。
b.数形结合思想。数形结合在导数及其应用部分的主要表现是对函数图像的分析与求解。函数是导数的主要研究对象之一,研究函数的性质经常用到数形结合思想。在导数及其应用的教学中可以很自然地渗透数形结合思想。
③数学思维方式的渗透
在“导数”部分主要的数学思维方式有两种:观察法和归纳法。
导数及其应用部分主要培养学生的观察能力。人教版教材利用三个不同维度的观察使得学生在导数的概念、导数的运算、导数的应用之间关系的思考。
归纳法是从特殊到一般再到特殊的过程,在人教版教材中主要体现在当△x趋于0的计算。
(2)①有利于激发学生的学习兴趣
数学文化给学生带来的不仅仅是数学命题、数学方法、数学问题和数学语,还包括数学思想、数学意识、数学精神等。在教学中可以适当地对学生进行数学文化的教育,如通过数学家的故事,数学问题的发现等内容的介绍来激发学生的学习兴趣。
②有利于培养学生的创新意识和探索精神
新一轮数学改革的理念中,强调培养学生的创新意识和探索精神。培养学生的数学思维能力,也是当代数学教育改革的核心问题之一。在数学文化中数学历史事件、历史过程、历史故事都能够激发起学生的创新意识,培养学生的探索精神。
③有利于发展学生的数学应用意识
数学文化的意义不仅在于知识本身和它的内涵,还在于它的应用价值。数学源于生活,其理论的核心部分都是在人类社会的生产、生活实践中发展起来的。因此,教学中应当有意识地结合学生已有的知识结构,加强数学与实际生活的联系,将数学知识生活化,让学生感受到生活的各个领域中都要用到数学,从而更深切的感受数学文化的价值。 -
第5题:
请举例分析小学数学课堂学习中的认知建构的活动过程。
正确答案: 它是一种由三个基本环节组成的环状结构。包括:定向环节,属于“输入系统”、行动环节,属于“输出系统”、反馈环节,属于“回归式内导系统”。 -
第6题:
《幼儿园教育指导纲要》中数学领域的目标是()。
- A、能运用各种感官,动手动脑,探究问题
- B、能够学习数学文化知识
- C、能体验到数学的重要和有趣
- D、引导幼儿对身边常见事物和现象产生兴趣
正确答案:C -
第7题:
下列不属于开设数学文化课,学生收获的是()
- A、了解数学思想
- B、提高数学能力
- C、学会以数学的方式思
- D、都不对
正确答案:B -
第8题:
古罗马时代文化课程中的三艺是指()
- A、几何、数学、天文
- B、文法、修辞、辩证法
- C、语文、数学、外语
- D、文法、数学、辩证法
正确答案:B -
第9题:
填空题数学具有()、应用价值和文化价值三大价值功能。正确答案: 科学价值解析: 暂无解析 -
第10题:
填空题数学探究、()、数学文化是贯彻于整个高中数学课程的重要内容,这些内容不单独设置,渗透在每个模块或专题中。正确答案: 数学建模解析: 暂无解析 -
第11题:
单选题要引起对数学的兴趣,需要了解()。A数学历史
B数学文化
C数学方法
D数学思想
正确答案: C解析: 暂无解析 -
第12题:
单选题以下不属于数学文化的侠义意思的是()A数学思想
B数学精神
C数学方法
D数学教育
正确答案: B解析: 暂无解析 -
第13题:
《普通高中数学课程标准(实验)》将“( )、数学建模、数学文化”作为贯穿整个高中数学课程的重要学习活动,渗透或安排在每个模块或专题中,正是与创新能力培养的一个呼应,强调如何引导学生去发现问题、提出问题。A.数学探究
B.数学应用
C.数学思想
D.数学概念答案:A解析: -
第14题:
数学应用是贯穿高中数学课程的一条主线,其应用主线结构图如下图所示: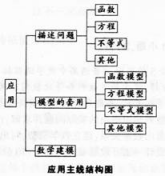
20世纪中叶以来,由于计算机和现代信息技术的飞速发展,使应用数学和数学应用得到了前所未有的发展,数学渗透到几乎每一个学科领域和人们日常生活的每一个角落。数学应用的巨大发展成为数学发展的显著特征之一。
(1)请举例说明高中数学内容在现实生活中的原型。
(2)分析高中数学教学中存在的问题。答案:解析:(1)函数有丰富的实际背景,出租车的计价、邮局寄包裹的计费都是分段函数的实际应用:考古学中也应用到了指数函数的性质;简谐振动的数学模型就是三角函数;平抛运动抽象为数学模型就是二次函数。
又例如:储蓄中的单利问题是等差数列模型,复利问题是等比数列模型。
算法中的取最小值问题、排序问题都是实际中常见的。
生活中的掷硬币决胜负、抽签决定出场次序都是概率模型在生活中的应用。
在研究力和速度时,向量就是很好的模型。
宇宙天体的运行轨道、铅球出手后的运动轨迹、汽车的广角灯等,都是圆锥曲线模型在实际中的应用。
通过这些实际例子,可以帮助我们更深刻地理解数学中的重要概念,有了对于这些重要概念(模型)的本质理解,就可以更好地利用这些模型来刻画(描述)实际问题。
(2)在我国数学教学中,比较突出的一个问题是忽视数学的应用,忽视数学与其他学科以及与日常生活的联系,忽视培养学生的应用意识。在很长一段时期内,数学教育界过分强调“数学是思维的体操”。把数学应用斥之为“实用主义”“短视行为”。1995年以后,虽然数学应用的呼声渐高,但是数学课程中对数学应用的重视程度还是比较低的。由于数学课程与教学中对数学应用的忽视,使学生在数学学习中,不能足够地认识到数学的应用价值、数学与日常生活以及其他学科的联系。 -
第15题:

20世纪中叶以来,由于计算机和现代信息技术的飞速发展,使应用数学和数学应用得到了前所未有的发展,数学渗透到几乎每一个学科领域和人们日常生活的每一个角落。数学应用的巨大发展成为数学发展的显著特征之一。
(1)请举例说明高中数学内容在现实生活中的原型。
(2)分析高中数学教学中存在的问题。答案:解析:(1)函数有丰富的实际背景,出租车的计价、邮局寄包裹的计费都是分段函数的实际应用:考古学中也应用到了指数函数的性质;简谐振动的数学模型就是三角函数;平抛运动抽象为数学模型就是二次函数。
又例如:储蓄中的单利问题是等差数列模型,复利问题是等比数列模型。
算法中的取最小值问题、排序问题都是实际中常见的。
生活中的掷硬币决胜负、抽签决定出场次序都是概率模型在生活中的应用。
在研究力和速度时,向量就是很好的模型。
宇宙天体的运行轨道、铅球出手后的运动轨迹、汽车的广角灯等,都是圆锥曲线模型在实际中的应用。
通过这些实际例子,可以帮助我们更深刻地理解数学中的重要概念,有了对于这些重要概念(模型)的本质理解,就可以更好地利用这些模型来刻画(描述)实际问题。
(2)在我国数学教学中,比较突出的一个问题是忽视数学的应用,忽视数学与其他学科以及与日常生活的联系,忽视培养学生的应用意识。在很长一段时期内,数学教育界过分强调“数学是思维的体操”。把数学应用斥之为“实用主义”“短视行为”。1995年以后,虽然数学应用的呼声渐高,但是数学课程中对数学应用的重视程度还是比较低的。由于数学课程与教学中对数学应用的忽视,使学生在数学学习中,不能足够地认识到数学的应用价值、数学与日常生活以及其他学科的联系。 -
第16题:
函数知识一直是中学代数内容的主线。是研究代数、三角函数、数列、方程和不等式等初等数学内容的基础,函数思想又是数学解题中的重要思想,这就决定了函数在中学数学中的重要地位。
请说明初中函数内容教学的要求,并结合自己的教学,谈谈利用函数思想解决问题时,重点要注意的问题是什么 并举出两个你印象最为深刻的利用函数思想解题的例子。答案:解析:初中函数的要求:①能探索具体问题中的数量关系和变化规律;②了解常量、变量的意义,了解函数概念和表示方法;③能结合图象分析,能用适当函数表示刻画某些实际问题中变量之间的关系;④对具体的一次函数、二次函数、反比例函数体会意义,画出图象,确定解析式、能利用函数解决一些实际问题。
利用函数思想解决问题时要注意的问题是:①函数知识的横向、纵向联系;②把函数、方程、不等式看成一个整体:③将函数性质、特征与图象紧密结合;④二次函数的综合运用;⑤实际问题通过建立函数模型解决等。 -
第17题:
数学文化主要是关于()的课程。
- A、数学知识
- B、数学理论
- C、数学应用
- D、数学思想
正确答案:D -
第18题:
数学具有()、应用价值和文化价值三大价值功能。
正确答案:科学价值 -
第19题:
1998年以后,教育部的专业目录里规定了数学学科专业,包括数学与应用数学专业、()。
- A、统计学
- B、数理统计学
- C、信息与计算科学专业
- D、数学史与数学文化
正确答案:C -
第20题:
以下不属于数学文化的侠义意思的是()
- A、数学思想
- B、数学精神
- C、数学方法
- D、数学教育
正确答案:D -
第21题:
单选题1998年以后,教育部的专业目录里规定了数学学科专业,包括数学与应用数学专业、()。A统计学
B数理统计学
C信息与计算科学专业
D数学史与数学文化
正确答案: A解析: 暂无解析 -
第22题:
单选题数学文化主要是关于()的课程。A数学知识
B数学理论
C数学应用
D数学思想
正确答案: B解析: 暂无解析 -
第23题:
填空题高中数学课程提倡体现数学的文化价值,并在适当的内容中提出对()的学习要求,设立“数学史选讲”等专题。正确答案: 数学文化解析: 暂无解析
