如图3，△ABC向右平移后得到△DEF，且点B、C、E、F在同一直线上，已知BF=8，CE=2，则平移的距离是__________。

题目
如图3，△ABC向右平移后得到△DEF，且点B、C、E、F在同一直线上，已知BF=8，CE=2，则平移的距离是__________。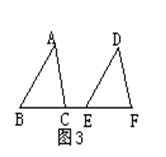

相似考题

1.已知△ABC∽△DEF，且AB：DE=1：2，则△ABC的面积与△DEF的面积之比为(A)1：2 (B)1：4 (C)2：1 (D)4：1

2.一力作平行移动后，新作用点上的附加力偶一定( )。A 存在且与平移距离有关;B 存在且与平移距离无关;C 不存在;D 等于零。

3.如图所示，该图标表示什么信号?A.向左水平移动B.向右水平移动C.向前水平移动D.向后水平移动

4.一个力作平行移动后,新点的附加力偶矩一定()A、存在B、存在且与平移距离有关C、不存在D、存在且与平移距离无关

参考答案和解析
答案：
解析：
5
更多“如图3，△ABC向右平移后得到△DEF，且点B、C、E、F在同一直线上，已知BF=8，CE=2，则平移的距离是__________。”相关问题

  • 第1题：

    任画一个Rt△ABC，其中∠B=90°，分别作出△ABC按如下

    条件旋转或平移后的图形：

    1）以B点为旋转中心，按逆时针方向旋转30°；

    2）以B点为旋转中心，按逆时针方向旋转180°；

    3）取三角形外一点P为旋转中心，按逆时针方向旋转180°；

    4）将△ABC平移，使得B点的对应点为A点。

  • 第2题：

    如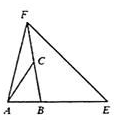，已知AE=3AB，BF=2BC。若ΔABC的面积是2，则ΔAEF的面积为

    A.14
    B.12
    C.10
    D.8
    E.6

    答案：B
    解析：
    因为是等高三角形，故面积比等于底边比.BF=2BC，.△ABF=2S△ABC=4 AE=3AB，.△AEF=3S△ABF=12故选B

  • 第3题：

    如图所示，一焦距为f的凸透镜，主轴和x轴重合。x轴上有一光点位于透镜的左侧，光点到透镜的距离在f和2f之间。若将此透镜沿x轴向右缓慢平移2f的距离，则在此过程中，光点经透镜所成的像点将( )。


    A．一直向右移动
    B．一直向左移动
    C．先向左移动．接着向右移动
    D．先向右移动．接着向左移动

    答案：C
    解析：
    点光源到透镜的距离大于，而小于2f，若将此透镜沿x轴向右平移2f的距离，点光源一直在凸透镜的一倍焦距以外，成倒立的实像。经凸透镜成实像时，点光源在二倍焦距处物像之间的距离最小。在透镜向右移动2f距离的过程中，物点到透镜的距离由大于f而小于2f增大到2f，，再增大到大于2f则物像间距应先减小后增大，由于物点静止不动，像点应先向左移动，接着向右移动，得正确答案C。

  • 第4题：

    将抛物线 向左平移4个单位后，再向下平移2个单位，则所得到的抛物线的解析式为（　　　）.


    答案：B
    解析：

  • 第5题：


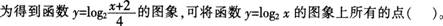    A.向左平移2个单位长度，再向上平移2个单位长度
    B.向右平移2个单位长度，再向上平移2个单位长度
    C.向左平移2个单位长度，再向下平移2个单位长度
    D.向右平移2个单位长度，再向下平移2个单位长度

    答案：C
    解析：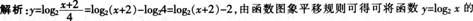

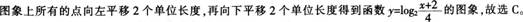
  • 第6题：

    在一条直线上有A、B两点，已知A、B点之间的水平距离是18m，A点高程是8m，B点高程是2m，则该直线的平距是1/3。


    正确答案:错误

  • 第7题：

    在Word的编辑状态下，打开文档ABC，修改后另存为DEF，则（）

    • A、ABC是当前文档
    • B、DEF是当前文档
    • C、ABC和DEF均是当前文档
    • D、ABC和DEF均不是当前文档

    正确答案:A

  • 第8题：

    在IS-LM模型中，增加已经退休人员的养老金的后果是（）。

    • A、IS曲线向右平移
    • B、LM曲线向右平移
    • C、IS曲线向左平移
    • D、LM曲线向左平移

    正确答案:A

  • 第9题：

    刚体平移时，若刚体上任一点的运动已知，则其它各点的运动随之确定。


    正确答案:正确

  • 第10题：

    填空题
    已知△ABC～△DEF，△ABC与△DEF的相似比为4：1，则△ABC与△DEF对应边上的高之比为____．

    正确答案： 4:1
    解析：
    由相似三角形的性质，相似三角形的对应线段的比等于相似比．

  • 第11题：

    单选题
    如图2-3所示，在空气中做牛顿环实验，当平凸透镜垂直向上缓慢平移而远离平面玻璃时，可以观察到这些环状干涉条纹（）。
    A

    向右平移

    B

    静止不动

    C

    向外扩张

    D

    向中心收缩


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    在IS-LM模型中，增加已经退休人员的养老金的后果是（）。
    A

    IS曲线向右平移

    B

    LM曲线向右平移

    C

    IS曲线向左平移

    D

    LM曲线向左平移


    正确答案： B
    解析： 暂无解析

  • 第13题：

    已知两个共用一个顶点的等腰Rt△ABC，等腰Rt△CEF，∠ABC=∠CEF= 90o，连接AF，M是AF的中点，连接MB，ME。
    (1)如图1，当CB与CE在同一直线上时，若CB=a，CE=2a，求BM，ME的长；
    (2)如图2,当∠BCE=45o时，求证：BM=ME。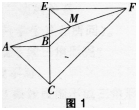



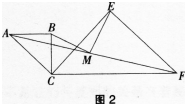    答案：
    解析：
    (1)如图，延长AB交CF于点D，则易知△BCD为等腰直角三角形，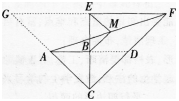


    (2)如图，延长AB交CE于点D，连接DF，则△BCD为等腰直角三角形，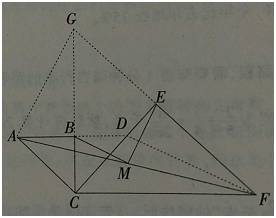


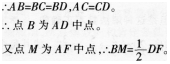
    延长FE与CB交于点G，连接AG，则易知△CEG为等腰直角三角形，
    ∴CE=EF=EG，CF=CG。
    ∴点E为FG中点。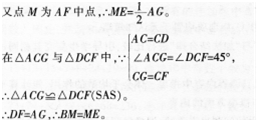

  • 第14题：

    如图所示，一焦距为 的凸透镜，主轴和x轴重合。x轴上有一光点位于透镜的左侧，光点到透镜的距离在 和2 之间。若将此透镜沿戈轴向右缓慢平移2 的距离，则在此过程中，光点经透镜所成的像点将（　　）。


    A．一直向右移动

    B．一直向左移动

    C．先向左移动.接着向右移动

    D．先向右移动，接着向左移动

    答案：C
    解析：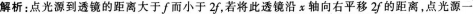

  • 第15题：

    小学数学《平移》
    一、考题回顾



    二、考题解析
    【教学过程】
    (一)导入新课
    老师做关窗、拉黑板的动作。
    提问：同学们，你们知道这些是什么现象吗? 引导学生说出：这是平移现象。
    追问：你还能说出生活中有哪些关于平移的现象?学生答：升旗，缆车，火车在笔直的铁轨上开等。
    (二)生成新知
    (1)课件出示教材中的例题1图。
    先让学生说出虚线部分和实线部分表示的是什么意思。
    提出问题：下面的小船图和金鱼图分别是怎样运动的?它们的运动有什么相同点和不同点?
    (2)教师动画演示小船图和金鱼图运动的过程，让学生观察，感受平移，并强调平移的方向。
    提问：小船图和金鱼图都进行了平移，它们是朝哪个方向平移的呢?学生观察得出：小船图和金鱼图都是向右平移。
    讲解概念：
    (1)认识平移的距离。
    提问：小船图和金鱼图都是向右平移，它们的运动有什么不同吗?引导学生发现：小船图平移的距离比金鱼图远一些，并数一数。(引导：数一数，小船图向右平移了几格?)小组交流讨论，教师巡视，进行纠错。之后组织全班交流。师质疑：有位同学数出两艘小船之间的距离是4格，他认为平移的距离就是4格，你觉得对吗?引导学生得出：4格只是两艘小船之间的距离，而不是小船平移的距离。追问：刚才同学们在小组内交流了怎样数平移了几格的方法，谁来和大家分享一下，你是怎么数的?
    引导学生进行汇报交流，学生可能会出现不同的数法，教师可以组织全班同学进行评价和判断，必要时让学生上台演示自己数的方法。
    数法预设：
    方法一：看船帆上的一条线段，这条线段向右平移了9格，小船图就向右平移9格。
    方法二：看船头的一个点，这个点向右平移了9格，小船图就向右平移9格。
    (2)数一数：金鱼图向右平移了几格?再与同学交流。 先让学生独立完成，再组织交流，教师巡视。
    (3)小结确定平移的距离的方法。
    先让学生说说，教师再结合学生的发言进行小结：我们在确定图形平移的距离时，可以先找出参照点，看它向哪个方向平移了几格，这个图形就向那个方向平移了几格。
    (三)应用新知
    完成教材中的“试一试”。
    (1)学生独立画图。
    教师巡视，了解学生存在的问题，对个别有困难的学生进行适当辅导。
    (2)组织汇报。
    学生一边用投影展示画出的图形，一边汇报是怎么画的。
    师根据学生的汇报小结画法：一种方法是先确定平行四边形的四个顶点，找出每个顶点平移后的对应点，再将这四个对应点依次连接起来;另一种方法是找每条边平移后的对应边。
    (四)小结作业
    小结：通过这节课的学习，你有什么收获?你对今天的学习还有什么疑问吗?
    作业：想一想，生活中还有哪些是平移的现象?
    【板书设计】



    【答辩题目解析】
    1.在本节课的教学过程中，你是如何引导同学们正确画出平移后的图形?
    2.教材中为什么要采用方格图?


    答案：
    解析：
    1、1.动态呈现平移过程，明白移动几格的意思。
    在平移的过程中，学生很容易对移动几格产生错觉，会错误地把移动的格数理解成两个图形中间的空格格数。教学中可以通过课件动态的展示平移过程，使学生通过观察，了解平移的方向和平移的距离分表示什么意思;也可以利用实物模型，按平移的要求实际操作，让学生体会平移的过程是整个图形按照要求进行平移，平移的距离是对应点之间的方格数，而不是平移前后两个图形之间的方格数。
    2.探索图形平移的画法，发展学生在方格纸上画平移图形的能力。
    第一、选点。也就是在原图形上选择几个能决定图形形状和大小的点。
    第二、移点。也就是按要求把选择的点向规定的方向平移规定的格数。
    第三、连点成形。

    2、方格图是学生学习轴对称、平移两种图形变换的重要工具，方格图上一条条水平和竖直的线，为学生建立方位感、感受距离提供有力的参照，是发展学生空间观念的重要途径和组成部分。这里的方格图不仅仅可以提供给学生简单的数据提示，以便成功地发现规律，还能够帮助学生在计算的基础上建立形的表象，帮助学生建立空间观念。方格图发挥了测量标准的重要作用，除了帮助学生发现和总结计算方法，更为学生理解和感受图形之间的联系起到了重要的作用。同时，方格图为学生提供实践的空间，使学生有了“做”数学、体验数学、经历数学的机会，有助于学生更好地学习数学知识，掌握数学学习方法。学生在这样的活动中，不仅仅收获了知识，也积累了测量的意识和方法，发展了空间观念。

  • 第16题：

    已知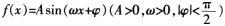

    的部分图象如图所示，则y=f(x)的图象向右平移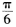

    个单位后得到的图象解析式为( )。



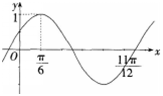
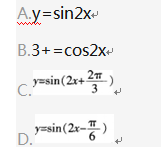    答案：D
    解析：
    由图可知该正弦函数最大值为1，故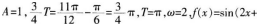

  • 第17题：

    如图，已知△ABC的两条角平分线AD和CE相交于H，∠B=60。，F在AC上，且AE=AF．
    (1)证明：B，D，H，E四点共圆；
    (2)证明：CE平分∠DEF．


    答案：
    解析：
    证明：(1)在△ABC中，因为∠B=60°，
    所以∠BAC+∠BCA=120°．
    因为AD，CE是角平分线．
    所以∠HAC+∠HCA=60°，故∠AHC=120°．
    于是∠EHD=∠AHC=120°．
    因为∠EBD+∠EHD=180°．所以B，D，H，E四点共圆．
    (2)连接BH，则BH为∠ABC的平分线，得∠HBD=30°，
    由(1)知B，D，H，E四点共圆，所以∠CED=∠HBD=30°．
    又∠AHE=∠EBD=60°，由已知AE=AF，AD平分∠EAF，
    可得EF⊥AD，所以∠CEF=30°．所以CE平分∠DEF．

  • 第18题：

    并网机组所带负荷减少时，静特性曲线（）。

    • A、向左平移
    • B、向右平移
    • C、向下平移
    • D、向上平移

    正确答案:A

  • 第19题：

    如果照相机的价格大幅度降低，则胶卷的需求曲线（）。

    • A、向左平移
    • B、向右平移
    • C、保持不变
    • D、发生扭曲

    正确答案:B

  • 第20题：

    当政府支出增加时，（）。

    • A、IS曲线向右平移
    • B、IS曲线向左平移
    • C、LM曲线向右平移
    • D、LM曲线向左平移

    正确答案:A

  • 第21题：

    如图2-3所示，在空气中做牛顿环实验，当平凸透镜垂直向上缓慢平移而远离平面玻璃时，可以观察到这些环状干涉条纹（）。

    • A、向右平移
    • B、静止不动
    • C、向外扩张
    • D、向中心收缩

    正确答案:D

  • 第22题：

    单选题
    当政府支出增加时，（）。
    A

    IS曲线向右平移

    B

    IS曲线向左平移

    C

    LM曲线向右平移

    D

    LM曲线向左平移


    正确答案： A
    解析： 暂无解析

  • 第23题：

    填空题
    将点A(2，4)按向量a＝(－5，－2)平移后，所得到的对应点A′的坐标是____．

    正确答案： (-3,2)
    解析：
    (2－5，4－2)＝(－3，2)．

相关内容