三次函数y=aχ3+bχ2+cχ+d的导函数图象如图l. 则此三次函数的图象是( )。
题目
三次函数y=aχ3+bχ2+cχ+d的导函数图象如图l. 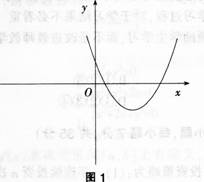 则此三次函数的图象是( )。
则此三次函数的图象是( )。
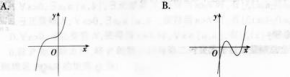

 则此三次函数的图象是( )。
则此三次函数的图象是( )。
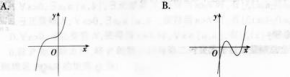

相似考题
参考答案和解析
答案:B
解析:
若f(x)在某个区间I内有导数,则f(x)≥0,(x∈I)<=>f(x)在I内为增函数:f’(x)≤O,x∈I<=>f(x)在I内为减函数。结合图I中导函数的函数值从左到右依次大于0、小于0、大于0,因此原函数图 象从左到右变化趋势依次是单调递增、单调递减、单调递增。因此选B。
更多“三次函数y=aχ3+bχ2+cχ+d的导函数图象如图l. 则此三次函数的图象是( )。 ”相关问题
-
第1题:
画出函数 y=x²-2x-3的图象,利用图象回答:
(1)方程 x²-2x-3=0 的解是什么;
(2)x取什么值时,函数值大于0 ;
(3)x取什么值时,函数值小于0 。
-
第2题:
已知一次函数的图象经过点A(2,1),B(-1,-3)
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积。
正确答案:(1)y=
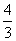 x -
x - 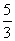
(2)与x轴的交点坐标(
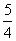 ,0);与y轴的交点坐标(0,-
,0);与y轴的交点坐标(0,- 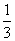 )
)(3)面积为
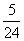
-
第3题:
当a≠0时,函数y=ax+1与y=a/x在同一坐标中图象可能是()。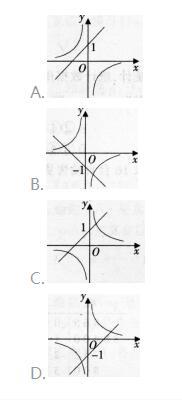 答案:C解析:
答案:C解析:
-
第4题:
定义[a,b,c]为函数y=ax2+bc+c的特征数,下面给出特征数为[ 2m ,1-m,-1-m]的函数的一些结论:
①当m=-3时,函数图象的顶点坐标是{1/3,-(8/3)};
②当m>0时,函数图象截石轴所得的线段长度大于3/2;
③当m<0时,函数在x>1/4时,y随x的增大而减小;
④当m≠0时,函数图象经过同一个点。
其中正确的结论有()。A.②③④
B.①②④
C.③④
D.②④答案:D解析:特征数[2m,1-m,-l-m]的函数为y=2mx2+(1-m)x+(-1-m)。①当m=-3时,y=-6x2+4x+
-
第5题:
下列函数图象与y=f(x)的图象关于原点对称的是( )A.y=-f(x)
B.y=f(-x)
C.y=-f(-x)
D.y=|f(x)|答案:C解析: -
第6题:
函数y(x)的导函数f(x)的图象如图所示,Xo=-1,则( )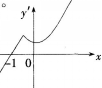 A、X。不是驻点
A、X。不是驻点
B、x。是驻点,但不是极值点
C、x。是极小值点
D、 X。极大值点答案:C解析:由图可知
f,+(‰)>0,一(‰)<0且f(x)在x连续可导,故xo为极小值点。 -
第7题:
光滑函数f(χ)的图象如图所示,下列关系式正确的是( )。 答案:B解析:
答案:B解析: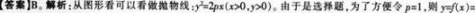

-
第8题:
三次函数r=ax3+bx2+cx+d的导函数图象如图1,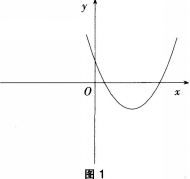 则此三次函数的图象是( )。
则此三次函数的图象是( )。
A.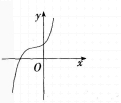
B.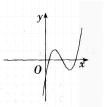
C.
D. 答案:B解析:若f(x)在某个区间,内有导数,则
答案:B解析:若f(x)在某个区间,内有导数,则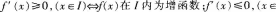
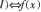 在,内为减函数。结合图1中导函数的函数值从左到右依次大于0、小于0、大于0,因此原函数图象从左到右变化趋势依次是单调递增、单调递减、单调递增。因此选B。
在,内为减函数。结合图1中导函数的函数值从左到右依次大于0、小于0、大于0,因此原函数图象从左到右变化趋势依次是单调递增、单调递减、单调递增。因此选B。 -
第9题:
由函数y=ex的图象与y=-2x,x=1,x=3所围成的封闭面积为_______。 答案:解析:
答案:解析: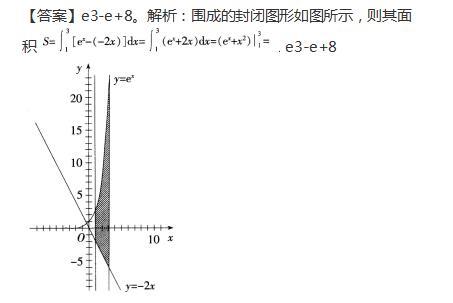
-
第10题:
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1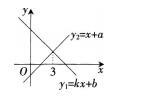 A.0
A.0
B.1
C.2
D.3答案:B解析:由一次函数y1=kx+b的图象可知,该函数在R上单调递减且与y轴的正半轴相交,由此可得k<0,b>0。同理,由一次函数y2=x+a的图象可知,该函数与y轴的负半轴相交,可得a<0。当x<3时,y1=kx+b的图象始终在,y2=x+a图象的上方,所以y1>y2。所以题中结论正确的只有①。 -
第11题:
已知函数 (x)=sin(ωx+φ)(ω>0)的图象如下图所示,则ω=( )。
 答案:B解析:
答案:B解析:
-
第12题:
填空题二次函数y=-x2+2x+n的图象与x轴的一个交点为(3,0),则n=____.正确答案: 3解析:
将(3,0)代人y=-x2+2x+n,得-32+2×3+n=0,解得n=3. -
第13题:
已知m是整数,且一次函数y=(m+4)x+m+2的图象不过第二象限,则m= ;
正确答案:
-3或-2 -
第14题:
 A.常数k<-1
A.常数k<-1
B.函数f(x)在定义域范围内,y随着x的增大而减小
C.若点C(-1,m),点B(2,n),在函数f(x)的图象上,则m<n
D.函数f(x)图象对称轴的直线方程是y=x答案:C解析:由图象可知常数k>0,A项错误;当x>0时,y随着x的增大而减小,当x<0时,y随着x的增大而减小,B选项说法不严谨,错误;由反比例函数的公式可得,m=-k<0,

m<n,C正确;函数f(x)图象对称轴有两条,y=x和y=-x,D错误。 -
第15题:
下图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
(1)求出图象与戈轴的交点A,B的坐标;
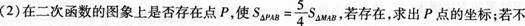
存在,请说明理由;
° (3)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.

答案:解析:解:(1)由二次函数Y=(x+m)2+k的顶点坐标为M(1,-4)可知,m=-1,k=-4.则二次函数Y=(x-1)2-4与x轴的交点为A(-1,0),8(3,0).
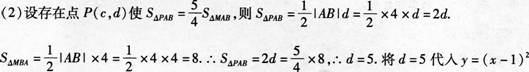
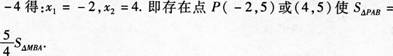
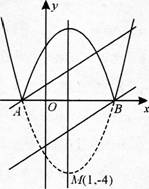
(3)如图,当直线Y=x+b经过A(-1,0)时-1+b=0,
可得b=1,又因为b<1,
故可知Y=x+b在Y=x+1的下方,
当直线Y=x+b经过点B(3,0)时,3+b=0,则b=-3,
由图可知,b的取值范围为-3<b<1时,
直线Y=x+b(b<1)与此图象有两个公共点.
-
第16题:
简支梁某段长度上受有均布载荷q,则该段粱的挠度y,是沿轴线的横坐标x的( )。A 五次函数
B 四次函数
C 三次函数
D 二次函数答案:B解析:由EIy"=-M(x)均布载荷时M(x)是x的二次函数积分两次后为四次函数 -
第17题:
函数y=2x-2的图象与坐标轴的交点共有__________个.答案:解析:2 -
第18题:
函数y=-χ·cos的部分图象是( )。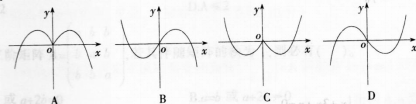 答案:D解析:函数y=-xcosx是奇函数,图象不可能是A和c,又当x∈(0,π/2)时,y<0,故选择D。
答案:D解析:函数y=-xcosx是奇函数,图象不可能是A和c,又当x∈(0,π/2)时,y<0,故选择D。 -
第19题:
函数y=-x·COS3f的部分图象是( )。
A.
B.
C.
D.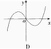
答案:D解析:
-
第20题:
关于二次函数y=2-(x+1)2的图象,下列说法正确的是( )。A.图象开口向上
B.图象的对称轴为直线x=1
C.图象有最低点
D.图象的顶点坐标(-1,2)答案:D解析:由二次函数图象的性质可知,其开口方向向下,有最大值2,对称轴为x=-1,顶点坐标(-1,2)。二次函数y=a(x+h)2+k(α≠0)中,α决定了二次函数图象的开口方向,顶点坐标为(-h,k)。 -
第21题:
若函数f(x)=(k-1)ax- ax (a>0且α≠1)在R上既是奇函数,又是减函数,则g(x)=loga (x+k)的图象是( )。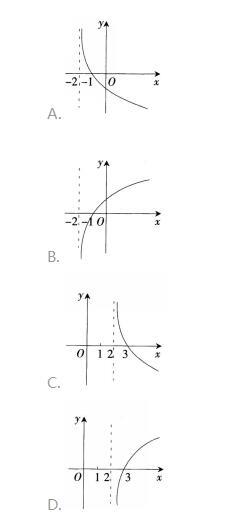 答案:A解析:函数f(x)是奇函数,则有f(0)=(k-1)-1=0,得k=2.f(x)=ax-a-x。又f(x)在R上是减函数,则有0
答案:A解析:函数f(x)是奇函数,则有f(0)=(k-1)-1=0,得k=2.f(x)=ax-a-x。又f(x)在R上是减函数,则有0第22题:
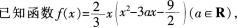
若函数f(x)的图象上点P(1,m)处的切线方程为3x-y+b=0,则m的值为__________。答案:解析:
第23题:
硬化曲线的函数表达式通常采用()。
- A、幂函数
- B、指数函数
- C、二次函数
- D、三次函数
正确答案:A
