在角、等边三角形、矩形和双曲线四个图形中,既是轴对称图形又是中心对称图形的有( )。A.1个 B.2个 C.3个 D.4个
题目
在角、等边三角形、矩形和双曲线四个图形中,既是轴对称图形又是中心对称图形的有( )。
A.1个
B.2个
C.3个
D.4个
B.2个
C.3个
D.4个
相似考题
更多“在角、等边三角形、矩形和双曲线四个图形中,既是轴对称图形又是中心对称图形的有( )。 ”相关问题
-
第1题:
下列平面图形中,即是轴对称图形又是中心对称图形的是( )

A.A
B.B
C.C
D.D
正确答案:B
-
第2题:
轴对称图形和两个图形成轴对称的区别和联系是什么?【数学专业问题】答案:解析:把成轴对称的两个图形看成一个整体,它就是一个轴对称图形。把一个轴对称图形沿着对称轴分成两个图形,这两个图形关于这条轴对称。
也就是,轴对称图形指的是一个图形;成轴对称图形指的是两个图形。 -
第3题:
在角、等边三角形、矩形和双曲线四个图形中,既是轴对称又是中心对称的图形有( )A.1个
B.2个
C.3个
D.4个答案:B解析:角是轴对称的图形,等边三角形是轴对称的图形,矩形既是轴对称又是中心对称的图形,双曲线既是轴对称又是中心对称的图形,所以共有2个符合题意。 -
第4题:
下列四个图形中,既是轴对称图形又是中心对称图形的有( )。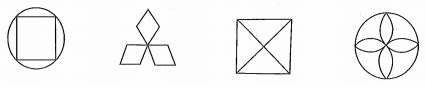 A.4个
A.4个
B.3个
C.2个
D.1个答案:B解析:第一、三、四图形既是轴对称图形又是中心对称图形,第二个图形是轴对称图形,但不是中心对称图形,故选B。 -
第5题:
下列图形中,既是轴对称图形,又是中心对称图形的是( )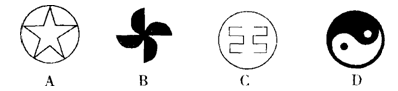 答案:C解析:
答案:C解析: -
第6题:
“中心对称和中心对称图形”的教学目的主要有①知道中心对称的概念,能说出中心对称的定义和关于中心对称的两个图形的性质。②会根据关于中心对称图形的性质定理2的逆定理来判定两个图形关于一点对称;会画与已知图形关于一点成中心对称的图形。此外,通过复习图形轴对称,并与中心对称比较,渗透类比的思想方法;用运动的观点观察和认识图形,渗透旋转变换的思想。
通过题干来完成下列教学设计。
(1)给出本课程的课题引入;
(2)根据教学目标设计教学环节;给出两个实例以进行知识探究。答案:解析:(1)课题引入:(引导性材料) 想一想:怎样的两个图形叫作关于某直线成轴对称成轴对称的两个图形有什么特点
(帮助学生复习轴对称的有关知识,为中心对称教学做准备)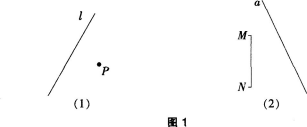
画一画:如图1(1),已知点P和直线ι,P出点P关于直线Z的对称点P′;如图1(2),已知线段MN和直线a,匦出线段MN关于直线a的对称线段M′N′。
(通过画图形进一步巩固和加深对轴对称的认识)
上述问题由学生回答,教师作必要的提示,并归纳总结成下表:
观察与思考:图2所示的图形关于某条直线成轴对称吗如果是,画出对称轴;如果不是,说明理由。
(教师把图2的两个图形制成投影片或教具,学生仔细观察后,能发现这两个图形都不是轴对称。然后,教师适时提出问题:这两个图形能不能重合怎样才能使这两个图形重合呢让学生观察、探究、讨论,教师可以直观地演示中心对称变换的过程,让学生发现:把其中一个图形统一特殊点旋转180度后能与另一个图形重合。)
问题1:你能举出1~2个实例或实物.说明它们也具有上面所说的特性吗
说明:学生自己举例有助于他们感性地认识中心对称的意义。然后,教师指出:具有这种特性的图形叫作中心对称图形.并介绍对称中心,对称点等概念。
问题2:你能给“中心对称”下一个定义吗
说明与建议:学生下定义会有困难,教师应及时修正,并给出明确的定义,然后指出定义中的三个要点:
①有一个对称中心——点;②图形绕中心旋转180度;③旋转后与另一图形重合。把这三要点填入引导性材料中的空表内,在顶空格内写上“中心对称”字样,以利于写“轴对称”进行比较。
(2)教学环节:
环节1:练一练:在图3中,已知△ABC和△EFG关于点O成中心对称,分别找出图中的对称点和对称线段。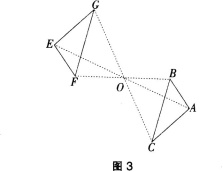
说明与建议:教师可演示△ABC绕点O旋转180度后与△EFG重合的过程,让学生说出点E和点A,点B和点F,点C和点G是对称点;线段AB和EF、线段AC和EG,线段BC和FG都是对称线段。教师还可向学生指出,上图中,点A、O、E在一条直线上,点C、O、G在一条直线上,点B、O、F在一条直线上,且AO=EO,BO=FO,CO=GO。
问题:从上面的练习及分析中,可以看出关于中心对称的两个图形具有哪些性质
说明与建议:引导学生总结出关于中心对称的两个图形的性质:定理1——关于中心对称的两个图形是全等形;定理2——关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
问题:定理2的题设和结论各是什么试说出它的逆命题。
说明与建议:学生解答此题有困难,教师要及时引导。特别是叙述命题时。学生常常照搬“对称点”“对称中心”这些词语,教师应指出:由于没有“两个图形关于中心对称”的前提。所以不能使用“对称点”“对称中心”这样的词语,而要改为“对应如”“某一点”。最后,教师应完整地叙述这个逆命题——如果两个图形的对应点连线都经过某一点,并且被这一点平分。那么这两个图形关于点对称。
问题:怎样证明这个逆命题是正确的
说明与建议:证明过程应在教师的引导下,师生共同完成。由已知条件——对应点的连线都经过某一点,并且被这一点平分,可以知道:若把其中一个图形绕着这点旋转180度,它必定与另一个图形重合,因此,根据定义可以判定这两个图形关于这一点对称。这个逆命题即为逆定理。根据这个逆定理,可以判定两个图形关于一点对称,也可以画出已知图形关于一点的对称图形。
环节2:练一练:画出图4中,线段PQ关于点O的对称线段P′Q′。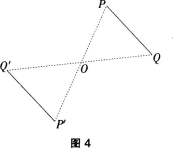
(画法如下:(1)连结PO,延长PO到P′,使OP′=OP,点P,就是点P关于点O的对称点。(2)连结QO,延长QO到Q′,使Q′Q=OQ,点Q′就是点Q的对称点,则PQ′就是线段PQ关于O点的对称线段。教师应指出:画一个
图形关于某点的中心对称图形,关键是画“对称点”。比如,画一个三角形关于某点的中心对称三角形,只要画出三角形三个顶点的对称点,就可以画出所要求的三角形。) -
第7题:
下列说法中,不正确的是( )。A.轴对称图形的对称轴是连接对称点线段的垂直平分线
B.中心对称图形的对称中心也是连接对称点线段的中点
C.矩形是以对角线为对称轴的轴对称图形
D.线段是以其中点为对称中心的中心对称图形答案:C解析:轴对称图形的对称轴是连接对称点线段的垂直平分线,故A项正确;中心对称图形的对称中心也是连接对称点线段的中点,故B项正确;矩形是轴对称图形,但它的对角线不是对称轴(正方形除外),故C项错误;线段是以其中点为对称中心的中心对称图形,故D项正确。故选C。 -
第8题:
如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做什么图形?()
- A、不对称
- B、中心对称
- C、骨式
- D、轴对称
正确答案:D -
第9题:
如果一个图形绕着一个点旋转180°后,能够和原图形完全重合,那么这个图形就叫做(),这个点就是它的对称中心。
- A、轴对称图形
- B、中心对称图形
- C、对称图形
正确答案:B -
第10题:
道路辅助标志的形状与颜色分别为()
- A、矩形;白底、黑字、黑边框、白色衬边
- B、正等边三角形;黄底、黑边框、黑图案
- C、圆形;白底、红圈、红杠、黑图形
- D、矩形;蓝底、白图形
正确答案:A -
第11题:
单选题若一个四边形,既是轴对称图形,又是中心对称图形,那么该图形一定是()A菱形
B平行四边形
C等腰梯形
正确答案: C解析: 暂无解析 -
第12题:
单选题道路辅助标志的形状与颜色分别为()。A矩形;白底、黑字、黑边框、白色衬边
B正等边三角形;黄底、黑边框、黑图案
C圆形;白底、红圈、红杠、黑图形
D矩形;蓝底、白图形
正确答案: A解析: 暂无解析 -
第13题:
下列图形中,是中心对称图形但不是轴对称图形的是( ).
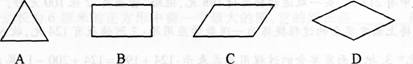 答案:C解析:平行四边形是中心对称图形,但不是轴对称图形.
答案:C解析:平行四边形是中心对称图形,但不是轴对称图形. -
第14题:
“中心对称和中心对称图形”的教学目的主要有①知道中心对称的概念,能说出中心对
称的定义和关于中心对称的两个图形的性质。②会根据关于中心对称图形的性质定理2的逆
定理来判定两个图形关于一点对称;会画与已知图形关于一点成中心对称的图形。此外,通过复习图形轴对称,并与中心对称比较,渗透类比的思想方法;用运动的观点观察和认识图形,渗透旋转变换的思想。
通过题干来完成下列教学设计。
(1)给出本课程的课题引入;
(2)根据教学目标设计教学环节;给出两个实例以进行知识探究。答案:解析:(1)课题引入:(引导性材料)
想一想:怎样的两个图形叫做关于某直线成轴对称 成轴对称的两个图形有什么特点
(帮助学生复习轴对称的有关知识,为中心对称教学作准备)
画一画:如图l(1),已知点P和直线l,画出点P关于直线,的对称点P,;如图l(2),已知线段MN和直线
a.画出线段MN关于直线a的对称线段M’N’。
(通过画图形进一步巩固和加深对轴对称的认识)
上述问题由学生回答.教师作必要的提示.并归纳总结成下表:
观察与思考:图2所示的图形关于某条直线成轴对称吗 如果是,画出对称轴,如果不是,说明理由。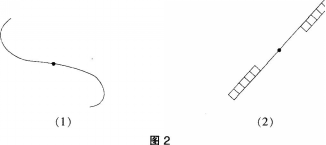
(教师把图2的两个图形制成投影片或教具,学生仔细观察后,能发现这两个图形都不是轴对称。然后,教师适时提出问题:这两个图形能不能重合 怎样才能使这两个图形重合呢 让学生观察、探究、讨论,教师可以直观地演示中心对称变换的过程,让学生发现:把其中一个图形统一特殊点旋转l80度后能与另一个图形重合。)
问题l:你能举出1~2个实例或实物,说明它们也具有上面所说的特性吗
说明:学生自己举例有助于他们感性地认识中心对称的意义。然后,教师指出:具有这种特性的图形叫做中心对称图形,并介绍对称中心,对称点等概念。
问题2:你能给“中心对称”下一个定义吗
说明与建议:学生下定义会有困难,教师应及时修正,并给出明确的定义,然后指出定义中的三个要点:
①有一个对称中心——点;②图形绕中心旋转l80度;③旋转后与另一图形重合。把这三要点填入引导性材料中的空表内,在顶空格内写上“中心对称”字样,以利于写“轴对称”进行比较。
(2)教学环节:
环节l:练一练:在图3中.已知AABC和AEFG关于点0成中心对称,分别找出图中的对称点和对称线段。
说明与建议:教师可演示△ABC绕点0旋转l80度后与△EFG重合的过程,让学生说出点E和点A,点B和点F,点C和点G是对称点;线段AB和EF、线段AC和EG,线段BC和FG都是对称线段。教师还可向学生指出,上图中,点A、0、E在一条直线上,点C、0、G在一条直线上,点8、0、F在一条直线上,且AO=E0,BO=F0,
CO=G0。
问题:从上面的练习及分析中,可以看出关于中心对称的两个图形具有哪些性质
说明与建议:引导学生总结出关于中心对称的两个图形的性质:定理l——关于中心对称的两个图形是全等形;定理2——关于中心对称的两个图形,对称点连线都经过对称中心.并且被对称中心平分。
问题:定理2的题设和结论各是什么 试说出它的逆命题。
说明与建议:学生解答此题有困难,教师要及时引导。特别是叙述命题时,学生常常照搬“对称点”“对称中心”这些词语,教师应指出:由于没有“两个图形关于中心对称”的前提.所以不能使用“对称点”“对称中心”这样的词语,而要改为“对应如”“某一点”。最后,教师应完整地叙述这个逆命题——如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于点对称。
问题:怎样证明这个逆命题是正确的
说明与建议:证明过程应在教师的引导下,师生共同完成。由已知条件——对应点的连线都经过某一点,并且被这一点平分,可以知道:若把其中一个图形绕着这点旋转180度,它必定与另一个图形重合,因此.根据定义可以判定这两个图形关于这一点对称。这个逆命题即为逆定理。根据这个逆定理,可以判定两个图形关于一点对称,也可以画出已知图形关于一点的对称图形。
环节2:练一练:画出图4中,线段PQ关于点D的对称线段PQ’。
(画法如下:(1)连结PD,延长PO到P,使0P'=OP,点P,就是点P关于点0的对称点。(2)连结Q0,延长Q0到Q’,使Q’Q=OQ,点Q’就是点Q的对称点,则PQ’就是线段PQ关于0点的对称线段。教师应指出:画一个图形关于某点的中心对称图形,关键是画“对称点”。比如,画一个三角形关于某点的中心对称三角形,只要画出三角形三个顶点的对称点,就可以画出所要求的三角形。) -
第15题:
四个图形:相交直线、等腰三角形、平行四边形、正多边形,既是轴对称又是中心对称的有( )个。A.1
B.2
C.3
D.4答案:A解析:相交直线既是轴对称又是中心对称图形,等腰三角形是轴对称图形,平行四边形是中心对称图形。正多边形当边数为奇数时是轴对称图形,当边数为偶数时既是轴对称又是中心对称图形。 -
第16题:
谈谈你对内容标准中“认识并欣赏自然界和现实生活中的轴对称、中心对称图形,运用图形的轴对称、旋转、平移进行图案设计”要求的认识。答案:解析:数学课程应通过具体内容的设置让学生体会并欣赏到数学的美,认识数学的应用,体会数学的价值;数学课程应通过恰当情境的创设,激发学生对数的好奇心和求知欲,使学生在积极、主动的教学活动中敢于发表自己的想法、勇于质疑,养成认真勤奋、独立思考、合作交流等学习习惯,形成实事求是的科学态度,感受成功的快乐,体验独自客服困难、解决数学问题的过程。内容标准在这些方面作了较好体现,如在图形与几何中“探究勾股定理及其逆定理,并能运用它们解决一些简单的实际问题”‘认识并欣赏自然界和现实生活中的轴对称、中心对称图形”“运用图形的轴对称、旋转、平移进行图案设计…‘通过建筑、艺术上的实例了解黄金分割”等。 -
第17题:
四个图形:相交直线、等腰三角形、平行四边形、正多边形,既是轴对称又是中心对称的有( )个。A、1
B、2
C、3
D、4答案:B解析:相交直线与正多边形既是轴对称又是中心对称图形。 -
第18题:
在等腰三角形、平行四边形、椭圆和抛物线四个图形中,是中心对称图形的有()。A.1个
B.2个
C.3个
D.4个答案:B解析:四个图形中,椭圆既是轴对称图形又是中心对称图形,平行四边形是中心对称图形,等腰三角形和抛物线是轴对称图形,所以这四个图形中有2个是中心对称图形。 -
第19题:
若一个四边形,既是轴对称图形,又是中心对称图形,那么该图形一定是()
- A、菱形
- B、平行四边形
- C、等腰梯形
正确答案:A -
第20题:
三角形衣架是我们日常生活用品,这些衣架都是有两个角相等,这样形成了一个轴对称图形,这个轴对称图形只有一条()
正确答案:对称轴 -
第21题:
某校计划修建一座既是中心对称图形又是轴对称图形的花坛,征集到的设计方案有等边三角形,正五边形,平行四边形,正八边形四种图案,你认为符合条件的是()
- A、等边三角形
- B、正五边形
- C、平行四边形
- D、正八边形
正确答案:D -
第22题:
单选题如果一个图形绕着一个点旋转180°后,能够和原图形完全重合,那么这个图形就叫做(),这个点就是它的对称中心。A轴对称图形
B中心对称图形
C对称图形
正确答案: A解析: 暂无解析 -
第23题:
单选题在AutoCAD对图形进行编辑中,用交叉窗口方式选取目标时,选中的图形为:()。A完全落入矩形方框的图形
B与方框边界相交的图形
C与方框边界相交及落入矩形方框的图形
D在程序窗口中显示的图形
正确答案: B解析: 暂无解析
