长为l的刚性轻质杆,一端固定在光滑的水平轴O处,另一端固定有小球,小球随杆在竖直平面内做圆周运动,如图所示。设小球在最高点的速度大小为v,重力加速度为g,若小球在最高点速度的大小可以取不同的值,则下列叙述正确的是( )。 A. v的取值由零开始增大时,杆对小球的作用力不变 B. v的取值由零开始增大时,杆对小球的作用力逐渐增大 C. v的取值由逐渐减小时。杆对小球的作用力逐渐减小 D. v的取值由逐渐增大时.杆对小球的作用力逐渐增大
题目
长为l的刚性轻质杆,一端固定在光滑的水平轴O处,另一端固定有小球,小球随杆在竖直平面内做圆周运动,如图所示。设小球在最高点的速度大小为v,重力加速度为g,若小球在最高点速度的大小可以取不同的值,则下列叙述正确的是( )。
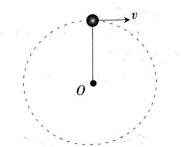
A. v的取值由零开始增大时,杆对小球的作用力不变
B. v的取值由零开始增大时,杆对小球的作用力逐渐增大
C. v的取值由
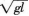
逐渐减小时。杆对小球的作用力逐渐减小
D. v的取值由
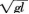
逐渐增大时.杆对小球的作用力逐渐增大

A. v的取值由零开始增大时,杆对小球的作用力不变
B. v的取值由零开始增大时,杆对小球的作用力逐渐增大
C. v的取值由
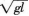
逐渐减小时。杆对小球的作用力逐渐减小
D. v的取值由
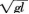
逐渐增大时.杆对小球的作用力逐渐增大
相似考题
更多“长为l的刚性轻质杆,一端固定在光滑的水平轴O处,另一端固定有小球,小球随杆在竖直平面内做圆周运动,如图所示。设小球在最高点的速度大小为v,重力加速度为g,若小球在最高点速度的大小可以取不同的值,则下列叙述正确的是( )。 ”相关问题
-
第1题:
如图所示质量为m、长为l的均质杆OA绕O轴在铅垂平面内作定轴转动。已知某瞬时杆的角速度为ω,角加速度为α,则杆惯性力系合力的大小为( )。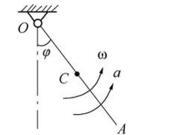
 答案:B解析:
答案:B解析:
-
第2题:
T形均质杆OABC以匀角速度ω绕O轴转动,如图所示。已知OA杆的质量为2m,长为2l,BC杆质量为m,长为l,则T形杆在图示位置时动量的大小为: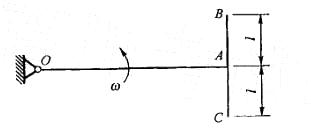
 答案:C解析:提示:动量 p=∑mivci=(2m?lω+m?2lω)j。
答案:C解析:提示:动量 p=∑mivci=(2m?lω+m?2lω)j。 -
第3题:
一细线拴着一小球,小球绕固定点在竖直平面内做圆周运动.设小球运动到最低点时所受细线拉力的大小为厂已知小球所受重力的大小为G,则( ) 答案:A解析:
答案:A解析: -
第4题:
如图5—17所示,在竖直平面内有一光滑的圆形轨道,轨道半径为尺,一个小球可在轨道内侧做圆周运动,且在通过圆周顶端的A点时不脱离轨道掉下来.
(1)小球通过A点的最小速度V0为多大
(2)在小球以速度V0通过A点的情况下,小球运动到B点时对轨道的压力F为多大 答案:解析:(1)小球以最小速度ν0通过A点时,向心力是仅由小球所受的重力提供的,由此得
答案:解析:(1)小球以最小速度ν0通过A点时,向心力是仅由小球所受的重力提供的,由此得
-
第5题:
 A.球进入竖直半圆弧轨道后做匀速圆周运动
A.球进入竖直半圆弧轨道后做匀速圆周运动
B.若小球能通过半圆弧最高点P,则球运动到P时向心力恰好为零
C.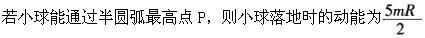
D.若小球恰能通过半圆弧最高点P,则小球落地点离O点的水平距离为2R答案:D解析:
-
第6题:
一个小球在竖直平面内的光滑圆环做圆周运动,小球经过圆环最高点时刚好不脱离圆环,通过最高点时,小球( )。A.没有受到向心力
B.向心力等于重力
C.没有向心加速度
D.线速度为0答案:B解析:
-
第7题:
以速度v0水平抛出一小球后,不计空气阻力,某时刻小球的竖直分位移与水平分位移大小相等,以下判断正确的是( )。A.此时小球的竖直分速度大小等于水平分速度大小
B.此时小球速度的方向与位移的方向相同
C.此时小球速度的方向与水平方向成450
D.从抛出到此时小球运动的时间为2v0/g答案:D解析:
-
第8题:
小球m用长为L的悬线固定在O点,在O点正下方处有一个光滑钉子C,如图所示,今把小球拉到悬线成水平后无初速度地释放.当悬线成竖直状态且与钉子相碰时()。
 答案:C解析:绳在竖直方向上与钉子相碰瞬间,绳子的拉力和重力都不对小球做功,即小球的动能不
答案:C解析:绳在竖直方向上与钉子相碰瞬间,绳子的拉力和重力都不对小球做功,即小球的动能不
-
第9题:
将一质量为m的小球靠近墙面竖直向上抛出,图甲是向上运动的频闪照片,图乙是下降时的频闪照片,0是运动的最高点,甲、乙两次的闪光频率相同,重力加速度为g,假设小球所受阻力大小不变,则可估算小球受到的阻力大小约为( )。

 答案:D解析:
答案:D解析:

-
第10题:
以下实例中的运动物体,机械能不守恒的是()
- A、抛出的钢球做斜抛运动
- B、用细绳拴着一个小球,绳的一端固定,使小球在竖直平面上做圆周运动
- C、物体沿着一个斜面匀速下滑
- D、用细绳拴着一个小球,绳的一端固定,使小球在光滑的水平面上做匀速圆周运动
正确答案:C -
第11题:
单选题A球进入竖直半圆弧轨道后做匀速圆周运动
B若小球能通过半圆孤最高点P.则球运动到P时向心力恰好为零
C若小球能通过半圆弧最高点P.则小球落地时的动能为5mgR/2
D若小球恰能通过半圆弧最高点P.则小球落地点离D点的水平距离为2R
正确答案: D解析: -
第12题:
单选题A球进入竖直半圆弧轨道后做匀速圆周运动
B若小球能通过半圆弧最高点P,则球运动到P时向心力恰好为零
C若小球能通过半圆弧最高点P,则小球落地时的动能为(5mgR)/2
D若小球恰能通过半圆弧最高点P则小球落地点离O点的水平距离为2R
正确答案: B解析: -
第13题:
均质细直杆OA长为l ,质量为m,A端固结一质置为m的小球(不计尺寸),如图所示。当OA杆以匀角速度w绕O轴转动时,该系统时O轴的动量矩为: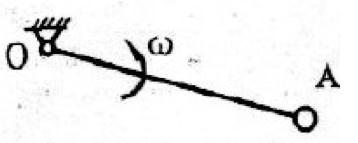
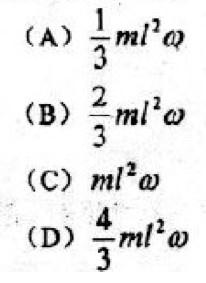 答案:D解析:
答案:D解析:
-
第14题:
物体用长为2的细绳挂着,在竖直平面内做圆周运动,当物体通过最高点时,速度至少是( )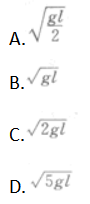 答案:B解析:
答案:B解析: -
第15题:
如图所示,重量为G、半径为R的小球,用长为R的细绳挂在光滑的竖直壁面A处,则细绳的拉力FT=__________,壁面对小球的弹力FN=__________. 答案:解析:1.15G,0.58G
答案:解析:1.15G,0.58G -
第16题:
如图1-10所示,细线的上端固定于O点,下端系一个小球P,线长l=
1.56 m,已知小球在水平面内做以O'为圆心的匀速圆周运动,悬线与竖直方向的夹角θ=45°.求
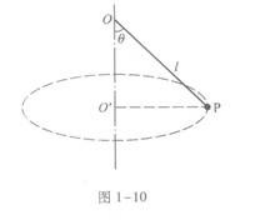 答案:解析:5.0 rad/s 【解题指要】本题是匀速圆周运动的试题,它的考点有牛顿第二定律和向心力.
答案:解析:5.0 rad/s 【解题指要】本题是匀速圆周运动的试题,它的考点有牛顿第二定律和向心力.
以小球为研究对象,小球受两个作用力,细线的拉力FT和重力G.FT沿细线向上,G竖直向下,图1-17是它的受力图.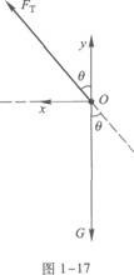
小球在水平面内做匀速圆周运动,它所受的合外力是匀速圆周运动的向心力.因此,重力G和拉力FT的合力就是向心力F.
取平面直角坐标如图所示.
FT的分量为
FTX=FTsinθ
FTY=FTcosθ
G的分量为
Gx=0
Gy=-mg
水平方向的牛顿方程为
FTx=FTsinθ=F=ma①
竖直方向的牛顿方程为
FTy+Gy=FTcosθ-mg=0
即FTy=FTcosθ=mg②
由式①、②解得
F=mgtanθ=ma
把向心加速度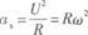
代入上式得
F=mRω2=mgtanθ
因此角速度为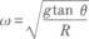
圆周运动半径R与线长l的关系是
R=lsinθ
代入上式解得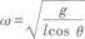
代入题给数值,算得
-
第17题:
如图所示,在竖直平面内有一光滑的圆形轨道,轨道的半径为R,一小球可在轨道内侧做圆周运动,且在通过圆周顶端的A点时不脱离轨道掉下来。则:
(1)小球通过A点的最小速度v0为多大?
(2)在小球以速度v0通过A点的情况下,小球运动到B点时对轨道的压力F为多大?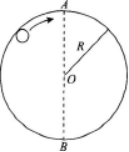 答案:解析:(1)小球以最小速度v0通过A点时,向心力是仅由小球所受的重力提供的,由此得
答案:解析:(1)小球以最小速度v0通过A点时,向心力是仅由小球所受的重力提供的,由此得
-
第18题:
如图所示,一根长为L的轻杆OA,0端用铰链固定,另一端固定着一个小球A.轻杆靠在一个质量为M、高为h的物块上,若物块与水平地面的摩擦力不计,当物块沿地面向右运动到杆与水平方向夹角为θ时,物块速度大小为v,此时小球A的线速度大小为( )。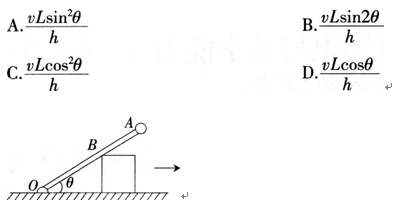 答案:A解析:当物块以速度V向右运动至杆与水平方向夹角为θ时,B点的线速度等于木块的速
答案:A解析:当物块以速度V向右运动至杆与水平方向夹角为θ时,B点的线速度等于木块的速
-
第19题:
小球m用长为L的悬线固定在O点,在O点正下方处有一个光滑钉子C,如图所示,今把小球拉到悬线成水平后无初速度地释放.当悬线成竖直状态且与钉子相碰时()。
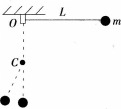 A.小球的线速度突然增大
A.小球的线速度突然增大
B.小球的角速度突然减小
C.小球的向心加速度突然增大
D.悬线的拉力突然减小答案:C解析:绳在竖直方向上与钉子相碰瞬间,绳子的拉力和重力都不对小球做功,即小球的动能不
-
第20题:
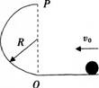
如图所示。小球沿水平面以初速度υo通过O点进入半径为R的竖直半圆弧轨道,不计一切阻力,下列说法正确的是( )。
A.球进入竖直半圆弧轨道后做匀速圆周运动
B.若小球能通过半圆弧最高点P,则球运动到P时向心力恰好为零
C.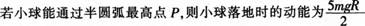
D.若小球恰能通过半圆弧最高点P,则小球落地点离O点的水平距离为2R
 答案:D解析:进入半圆弧轨道后,小球受到轨道的弹力和重力的作用,重力方向竖直向下,因此小球不能做匀速圆周运动,A错。小球能通过圆弧的最高点,因此速度必不为零,向心力也不为零,落地时的动能可能
答案:D解析:进入半圆弧轨道后,小球受到轨道的弹力和重力的作用,重力方向竖直向下,因此小球不能做匀速圆周运动,A错。小球能通过圆弧的最高点,因此速度必不为零,向心力也不为零,落地时的动能可能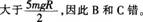
-
第21题:
如图所示,小球沿水平面以初速度v0通过O点进入半径为R的竖直半圆弧轨道,不计一切阻力,下列说法正确的是( )。
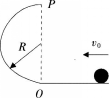
A.球进入竖直半圆弧轨道后做匀速圆周运动
B.若小球能通过半圆弧最高点P.则球运动到P时向心力恰好为零
C.若小球能通过半圆弧最高点P,则小球落地时的动能为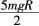
D.若小球恰能通过半圆弧最高点P,则小球落地点离O点的水平距离为2R答案:D解析:进入半圆弧轨道后,小球受到轨道的弹力和重力的作用,重力方向竖直向下,因此小球不能做匀速圆周运动,A错。小球能通过圆弧的最高点,因此速度必不为零,向心力也不为零,落地时的动能可能 大于
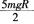
因此B和C错。 -
第22题:
从地面竖直上抛一个质量为m的小球,小球上升的最大高度为H.设上升过程中空气阻力为F恒定.则对于小球上升的整个过程,下列说法错误的是()
- A、小球动能减少了mgH
- B、小球机械能减少了FH
- C、小球重力势能增加了mgH
- D、小球加速度大于重力加速度g
正确答案:A -
第23题:
单选题长为l的刚性轻质杆,一端固定在光滑的水平轴0处,另一端固定有小球,小球随杆在竖直平面内做圆周运动,如图所示。设小球在最高点的速度大小为v,重力加速度为g,若小球在最高点速度的大小可以取不同的值,则下列叙述正确的是( )。Av的取值由零开始增大时,杆对小球的作用力不变
Bv的取值由零开始增大时,杆对小球的作用力逐渐增大
Cv的取值由根号gl逐渐减小时,杆对小球的作用力逐渐减小
Dv的取值由根号gl逐渐增大时.杆对小球的作用力逐渐增大
正确答案: C解析:
