“除数是小数的除法”,某老师把学生的回答的分12个馒头的计算板书出来:12÷3=4(人) 12÷2=6(人),12÷1=12(人),12÷0.5=24(人),这一做法体现了( )A.巩固性原则B.直观性原则C.理论联系实际原则D.因材施教原则
题目
“除数是小数的除法”,某老师把学生的回答的分12个馒头的计算板书出来:12÷3=4(人) 12÷2=6(人),12÷1=12(人),12÷0.5=24(人),这一做法体现了( )
A.巩固性原则
B.直观性原则
C.理论联系实际原则
D.因材施教原则
相似考题
参考答案和解析
理论联系实际原则是指教学要以学习基础知识为主导,从理论与实际的联系上去理解知识,注意运用知识去分析问题和解决问题,达到学懂会用、学以致用。故选C
更多““除数是小数的除法”,某老师把学生的回答的分12个馒头的计算板书出来:12÷3=4(人)12÷2=6( ”相关问题
-
第1题:
教学“除数是小数的除法”,某教师把分12个馒头的计算板书出来:12÷3=4(人),12÷2 =6(人),12÷0.5=24(人),这一做法体现了( )。 A.巩固性原则 B.直观性原则 C.理论联系实际原则 D.因材施教原则
正确答案:C
【考查要点】本题考查的知识点是“教学的基本原则”,这部分知识需要考生理解。
【名师详解】理论联系实际原则是指教学活动要把理论知识与生活和社会实践结合起来。题干中教师把理论知识与分馒头结合起来教学,解决了理论脱离实际的问题。
-
第2题:
某老师把学生回答平均分配12个馒头的多种计算方法板书出来:12÷3=4(人),12÷2=6(人),12÷1=12(人),12÷0.5=24(人),这一做法体现了( )。
A.巩固性原则
B.直观性原则
C.理论联系实际原则
D.因材施教原则
正确答案:C
这种做法体现了理论联系实际原则。 -
第3题:
在教授“除数是小数的除法”时,某老师把学生回答的如何分12个馒头的计算板书出 来:12÷3=4(人),12÷2 = 6(人),12÷1 = 12(人),12÷0.5 =24(人),这一做法体现了( )
A.巩固性原则 B.直观性原则
C.理论联系实际原则 D.因材施教原则答案:C解析:理论联系实际原则是指教师在教学中,应使学生从理论与实际的结合中来理解和掌握知识,并且 弓丨导他们运用新获得的知识去解决各种实际问题,培养他们分析问题和解决问题的能力。 -
第4题:
某老师把学生回答平均分配12个馒头的多种计算方法板书出来:12÷3=4(人),12÷2 = 6 (人),12÷1 = 12 (人),12÷4 = 3 (人),12÷6 = 2 (人),12÷0. 5 = 24 (人), 这一做法体现了( )。
A.巩固性原则 B.直观性原则 C.理论联系实际 D.因材施教原则答案:C解析:这种做法体现了理论联系实际原则。 -
第5题:
小李在计算有余数的除法时,把被除数113错写成131,结果商比原来多3,但余数恰巧相同,该题的余数是:
A.6 B.5 C.4 D.3答案:B解析:设余数是m、除数是y,则(131-m)÷y=(113-m)÷y+3,可得y=6。113÷6=18……5,则该题余数是5。 -
第6题:
小明和小强都是张老师的学生,张老师的生日是M月N日,2人都又知道张老师和生日是下列10组中的一天,张老师把M值告诉了小明,把N值告诉了小强,张老师问他们知道他的生日是那一天?
3月4日、3月5日、3月8日、6月4日、6月7日
9月1日、9月5IE]、12月1日、12月2日、12月8日
小明说:“如果我不知道的话,小强肯定也不知道。”小强说:“本来我也不知道,但现在我知道了。”小明说:“哦,那我也知道了。”请根据以上对话推断出张老师的生日是哪一天?( )
A.3月5日
B.6月4日
C.9月1日
D.12月2日答案:C解析:根据题意可知,3月、6月、9月、12月的日期有两个或两个以上,所以小明得知M后是不可能知道张老师的生日。6月7日、12月2日的日数是惟一的,如果小明得知的M值为6或12,又假若小强得知的N值为7或2,那么小强是可能知道张老师的生日的。而“小明说:‘如果我不知道的话,小强肯定也不知道。”’,由此可判断6月、12月的日期都不是张老师的生日。现在剩下3月4日、5日、8日,9月1日、5日五个日期,由“小强说:‘本来我也不知道,但现在我知道了。’”可知,小强的N值不等于5(3月5日和9月5日),因此N值可能为1、4或8,再由“小明说:‘哦,那我也知道了。”’可判断M值为9,N值为1(N为5已被排除,3月有两个日期)。 -
第7题:
小学数学《比的基本性质》
一、考题回顾
题目来源1月6日 下午 河南省开封市 面试考题
试讲题目1.题目:比的基本性质
2.内容:
?
3.基本要求:
(1)要有板书;
(2)试讲十分钟左右;
(3)条理清晰,重点突出;
(4)学生掌握比的基本性质。
答辩题目1.在本课的教学中主要运用的教学方法是什么?
2.请你叙述一下如何把小数之间的比化成简单的整数比?
二、考题解析
【教学过程】
(一)引入新课
复习比的概念,以及两个数的比还可以写成什么样的形式。比如6:8。并引导学生思考通常进行约分、通分是运用了分数的性质,那么比是不是也具有同样的性质呢?引出新课。
(二)探索新知
1.比的基本性质。
提问:我们通常进行约分、通分,是运用了分数的什么性质?这一性质和除法有什么关系呢?
预设:除法有商不变的性质:被除数和除数同时乘以或除以相同的数(0除外),商不变。被除数在分数中相当于分子,除数在分数中相当于分母,因此推出了分数的基本性质。
追问1:联系比和除法的关系,猜想一下,会不会存在类似商不变这样的规律呢?
学生以小组为单位,利用导入中的例子进行讨论:比的前项和后项及比值会有什么样的规律呢?
预设:
6÷8=(6×2)÷(8×2)=12÷16
6:8=(6×2):(8×2)=12:16
6÷8=(6÷2)÷(8÷2)=3÷4
6:8=(6÷2):(8÷2)=3:4
师生共同总结:比的前项、后项同时乘或除以相同的数(0除外),比值不变。
让学生类比刚刚的探究过程,接下来思考用比和分数的关系,运用刚才的研究方法,对比规律进行再一次的探索。
从而总结比的基本性质:比的前项、后项同时乘或除以相同的数(0除外),比值不变。
2.化简比的方法。
①让学生解决:求两面国旗的长和宽的最简整数比。
预设1:第一面联合国旗长和宽的比是15:10。利用比的基本性质,将前项、后项同时除以两个数的最大公因数。
预设2:第二面联合国旗长和宽的比是180:120。同样利用比的基本性质,将前项、后项同时除以两个数的最大公因数。
②化简比1/6:2/9 0.75:2
提问:怎样才能化为最简整数比?根据的是什么?
预设:将分数化成整数,然后进行化简。
追问:如果前项、后项出现了小数怎么办?当化简的比不是整数比时,应该怎么办?
预设:将小数化成整数,再进行化简。
(三)课堂练习
问题:小亮身高155cm,小红身高1m,两个人的身高比是多少?
提问:若前后项带有不同单位的比,应该怎样化简?
(四)小结作业
提问:今天有什么收获?
课后作业:课后相应练习题。
【板书设计】
比的基本性质
6÷8=(6×2)÷(8×2)=12÷16 练习:
6:8=(6×2):(8×2)=12:16
6÷8=(6÷2)÷(8÷2)=3÷4
6:8=(6÷2):(8÷2)=3:4
比的基本性质:比的前项、后项同时乘或除以
相同的数(0除外),比值不变。
1.在本课的教学中主要运用的教学方法是什么?
2.请你叙述一下如何把小数之间的比化成简单的整数比?答案:解析:1.
在教学中,导入部分我采用了复习导入的方法,回顾上节课学习的内容,为本课的学习奠定基础。
在新课教学环节,我采用情境教学方法,引入实际生活实例,更好的引起学生的兴趣。在讲授比的基本性质环节,我运用小组讨论的方法,目的是调动学生的积极性,参与到教学中来,把课堂还给学生,真正体现学生是课堂的主人。
2.
小数之间的比要先把小数化成整数,再进行计算,最后结果是两个数为互质数。如:0.25:0.4,0.25有两位小数,0.4有一位小数,两者化为整数的话,要同时乘以100才可以,(0.25×100):(0.4×100)=25:40=5:8。 -
第8题:
小刘和小红都是张老师的学生,张老师的生日是M月N日,两人都知道张老师的生日是下列10天中的一天,这十天分别为3月4日、3月5日、3月8日、6月4日、6月7日、9月1日、9月5日、12月1日、12月2日、12月8日。张老师把M值告诉了小刘,把N值告诉了小红,然后有如下对话:小刘说:如果我不知道的话,小红肯定也不知道小红说:刚才我不知道,听小刘一说我就知道了。小刘说:哦,那我知道了。请根据以上对话推断出张老师的生日是( )A.3月4日。
B.3月5日。
C.3月8日。
D.9月1日。
E.9月5日。答案:D解析: -
第9题:
在讲到“除数是小数的除法”这一部分的内容时,某老师把学生回答的关于分12个馒头的计算板书了出来:12÷4=3(人),12÷2=6(人),12÷1=12(人),12÷0.5=24(人)。这一做法体现了()。
- A、巩固性原则
- B、直观性原则
- C、理论联系实际原则
- D、因材施教原则
正确答案:C -
第10题:
教学“除数是小数的除法”,某教师把分12个馒头的计算板书出来:12÷3=4(人),12÷2=6(人),12÷0.5=24(人),这一做法体现了()。
- A、巩固性原则
- B、直观性原则
- C、理论联系实际原则
- D、因材施教原则
正确答案:C -
第11题:
某小学组织春游,若每位老师带5名学生,那么剩下12名学生没人带,如果每位老师带6名学生,那么刚好剩下3位老师。则参加春游的学生有多少()名?
- A、159
- B、162
- C、165
- D、172
正确答案:B -
第12题:
单选题在讲到“除数是小数的除法”这一部分的内容时,某老师把学生回答的关于分12个馒头的计算板书了出来:12÷4=3(人),12÷2=6(人),12÷1=12(人),12÷0.5=24(人)。这一做法体现了()。A巩固性原则
B直观性原则
C理论联系实际原则
D因材施教原则
正确答案: A解析: 该教师将抽象的数学计算与日常生活中的分馒头联系了起来,做到了理论与实际的结合。 -
第13题:
“除数是小数的除法”,某老师把学生分12个馒头的计算板书出来:12÷3=4(人),12÷2=6(人),12÷1=12(人),12-0.5=24(人),这一做法体现了( )。A.巩固性原则B.直观性原则C.理论联系实际原则D.因材施教原则
正确答案:C
引入馒头这一生活中的事物开展数学教学,阐释“除数是小数的除法”这一观念,充分体现了理论联系实际的原则。
-
第14题:
“除数是小数的除法”,某老师把学生的回答以分12个馒头的计算板书出来:12÷3=4 (人),12÷2=6(人),12÷l一12(人),12÷o。5=24(人),这一做法体现了
A.巩固性原则 B.直观性原则 C.理论联系实际原则 D.因材施教原则
正确答案:C老师在课堂教学的时候结合生活实践,引入馒头讲解、演算“除数是小数的除法”这一概念,显然是理论联系实际的原则。 -
第15题:
1999年5月的某一天,中学生蔡某趁着李老师写板书的间隙,偷偷躲在桌子下抽烟,李老师让蔡某交出来,蔡某坚持自己没抽烟。李老师非常气愤,狠狠地拧蔡某的耳朵,由于用力过猛,把蔡某的耳朵撕烂了一块,当场流血不止。李老师当时吓坏了,赶紧把蔡某送到医院进行治疗,并赔偿该同学的经济损失。
(1)李老师的行为违反了什么法律?需要承担什么责任?
(2)本案例对我们有哪些启示?答案:解析:(1)《中华人民共和国未成年人保护法》规定,教师应当尊重学生的人格,不得歧视学生,不得对学生实施体罚。李老师的行为侵犯了学生的生命权、身体权和健康权。学校应当给李老师处分。
(2)启示是教师需要加强对教育法律法规的学习,增强法律意识。 -
第16题:
教室里有50人在开会,其中学生35人,家长12人,老师3人,若校长站在门外听到有人发言,那么发言人是老师或学生的概率为( )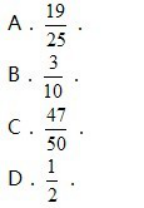 答案:A解析:
答案:A解析: -
第17题:
一次师生座谈会,老师看学生,人数一样多,学生看老师,老师的人数是学生的3倍,问老师和学生各有多少人?( )
A.24人,7人
B.3人,2人
C.18人,6人
D.6人,3人答案:B解析:根据题意设老师有x人,学生有Y人,则x-1=Y,3(y一1)=x,解得x=3,y=2。 -
第18题:
小学数学《整十整百的数除以一位数》
一、考题回顾

二、考题解析
【教学过程】
(一)新课导入
1.口答:20里面有( )个十,46里面有( )个十和( )个一,70里面有( )个十。
2.解决问题:把18支铅笔平均分给3个班,每个班分得几支?
口答算式:18÷3=6(支)
你是怎样想的?
学生交流,汇报。(把18支铅笔平均分成3份,每份是6支)
谈话:前面我们学习了运用乘法口诀求商,今天这节课,我们学习整十整百的数除以一位数的口算。(板书课题:整十整百的数除以一位数的口算)
(二)探索新知
1.教学整十数除以一位数
(1)3个20是60,60除以3等于20;
(2)6个十除以3得2个十,是20;
(3)6÷3=2,60÷3=20。
谈话:自己选择一种方法,把60÷3的算法再说一遍给同桌听。
小结:计算整十数除以一位数,可以把被除数看成几个十,再想一想这几个十除以除数等于多少个十;也可以用被除数十位上的数除以除数,商是几,最后算得的结果就是几个十。题目来源于考生回忆
2.教学整百数除以一位数
出示例1后的“试一试”:600÷3=
学生独立完成后,汇报交流。
小结计算方法:计算整百数除以一位数,可以把被除数看成几个百,再想几个百除以除数等于多少个百;也可以用被除数百位数上的数除以除数,商是几,最后算得的结果就是几个百。
3.教学几百几十除以一位数
出示教材例2,学生读题。
谈话:怎样列式?你能口算吗?
小组交流,汇报交流结果。
教师小结方法:口算几百几十除以一位数,可以把被除数看成几十几个十,再想几十几除以除数等于多少个十;也可以用被除数百位和十位上的数除以除数,商是多少,最后得到的结果就是多少个十。
(三)课堂练习
1.想想做做第1题
让学生自己说一说每组题在计算上的联系与区别,帮助学生形成算理。
小结方法:学生借助表内除非口算整十数、整百数除以一位数,只要在后面添相应个数的0.
2.想想做做第2题
指名学生口算,说说想法。
3.想想做做第3题
学生独立连线,集体订正交流。
4.想想做做第4题
提问:怎样求一个数是另一个数的几倍?(一个数除以另一个数)
学生独立完成,同桌互相检查。题目来源于考生回忆
(四)小结作业
提问:这节课你有什么收获?
作业:练习1、2、3。
【板书设计】

【答辩题目解析】
1.说说你本节课的教学目标是什么?
2.数学教学的板书作用是什么?答案:解析:1、根据本节内容在教材中的地位和作用,依据新课程标准的要求,以及三年级学生的认知结构和心理特征,本课时的教学力求达到以下目标:一、知识与技能方面:探索并掌握整百整十数的除法的口算方法,并能正确地计算;能结合具体情况进行估算,判断计算结果的对错,逐步养成验算的习惯。二、过程与方法方面:结合具体情境,发展提出问题和解决问题的意识和能力,体会到数学与生活的密切联系。三、情感态度与价值观方面:使学生经历与他人交流算法的过程,培养自主探索、合作交流和良好习惯。
2、板书是教学中重要的组成部分,是教学中最大众化的直观教具,也是教师进行教学活动的重要手段之一。板书可以帮助学生理解内容,理清条理,突出重点,突破难点;可以激发学生的学习兴趣;还可以培养学生抽象概括能力,培养学生的自学能力。本节课主要是是让学生掌握整十整百除以一位数的口算方法,板书上的标题和式子为了帮助学生理解内容和思路。 -
第19题:
补码定点小数除法中,被除数和除数应满足()。A.0≤|被除数|≤|除数|
B.O<|被除数|≤|除数|
C.0<|除数|≤被除数|
D.0<|被除数|<|除数|答案:B解析:
-
第20题:
在串行定点小数除法器中为了避免产生溢出,被除数的绝对值一定要小于除数的绝对值。
正确答案:正确 -
第21题:
“除数是小数的除法”,某老师把学生的回答的分12个馒头的计算板书出来:12÷3=4(人)12÷2=6(人),12÷1=12(人),12÷0.5=24(人),这一做法体现了()
- A、巩固性原则
- B、直观性原则
- C、理论联系实际原则
- D、因材施教原则
正确答案:C -
第22题:
“除数是小数的除法”,某老师把学生回答的分12个馒头的计算板书出来:12÷3=4(人),12÷2=6(人),12÷1=12(人),12÷0.5=24(人),这一做法体现了()。
- A、巩固性原则
- B、直观性原则
- C、理论联系实际原则
- D、因材施教原则
正确答案:C -
第23题:
问答题小刘和小红都是张老师的学生,张老师的生日是M月N日,2人都知道张老师的生日是下列10组中的一天,张老师把M值告诉了小刘,把N值告诉了小红,然后问他们老师的生日到底时哪一天? 3月4日、3月5日、3月8日、6月4日、6月7日、9月1日、9月5日、12月1日、12月2日、12月8日。 小刘说:如果我不知道的话,小红肯定也不知道。 小红说:刚才我不知道,听小红一说我知道了。 小刘说:哦,那我也知道了。 请根据以上对话推断出张老师的生日是哪一天?正确答案: 首先,我们来分析一下这10组日期,经观察不难发现,只有6月7日和12月2日这两组日期的日数是唯一的。由此可以看出,假如小红知道的N是7或者2,那么她肯定知道老师的生日时哪一天。
再次,我们来分析一下小刘说的话,小刘说:“如果我不知道的话,小红肯定也不知道”,而该10组日期的月数分别为3,6,9,12,而且相应月的日期都有两组以上,所以小刘得知M后是不可能知道老师生日的。
进一步分析,小刘说:“如果我不知道的话,小红肯定也不知道”,通过结论2我们可知小红得知N后也绝不可能知道。
然后,结合1和3的分析,可以推断:所有6月和12月的日期都不是老师的生日,因为如果小刘得知的M是6,而若小红的N=7,则小红就知道了老师的生日。
同样的道理,如果小刘的M=12,若小红的N=2,则小红同样可以知道老师的生日。即:M不等于6和9。现在只剩下“3月4日、3月5日、3月8日、9月1日、9月5日”五组日期。而小红知道了,所以N不等于5(有3月5日和9月5日),此时,小红的N∈(1,4,8)注:此时N虽然有三种可能,但对于小红只要知道其中的一种,就得出结论。所以有“小红说:本来我也不知道,但是现在我知道了”,通过这样的推理,最后就剩下“3月4日、3月8日、9月1日”三个生日。
分析“小刘说:哦,那我也知道了”,说明M=9,N=1,(N=5已经被排除,3月份的有两组)。因此正确答案应该是9月1日。解析: 暂无解析 -
第24题:
单选题“除数是小数的除法”,某老师把学生回答的分12个馒头的计算板书出来:12÷3=4(人),12÷2=6(人),12÷1=12(人),12÷0.5=24(人),这一做法体现了( )。A巩固性原则
B直观性原则
C理论联系实际原则
D因材施教原则
正确答案: C解析:
理论联系实际原则是指教学要以学习基础知识为主导,从理论与实际的联系上去理解知识,注意运用知识去分析问题和解决问题,达到学懂会用,学以致用。本题中,教师把数学运算用馒头来演示,属于理论联系实际原则。
