有一类数，每一个数都能被11整除，并且各位数字之和是20，问这类数中，最小的数是_______。

题目

有一类数，每一个数都能被11整除，并且各位数字之和是20，问这类数中，最小的数是_______。

相似考题

1.用2、3、4三个数字所组成的三位数，都能被3整除。（ ）

2.能被2整除的数叫做（ ），不能被2整除的数叫做（ ）。

3.一个六位数的各位数字都不相同，最左一位数字是3，且它能被11整除，这样的六位数中最小的是（ ）。 A．301245 B．301246 C．310254 D．310246

4.一个三位数能不能被3整除，只要看这个数的各位数字的和能不能被3整除，这是为什么？四位数能否被3整除是否也有这样的规律？你还能得到哪些结论？

参考答案和解析
正确答案：
1199
更多“有一类数，每一个数都能被11整除，并且各位数字之和是20，问这类数中，最小的数是_______。”相关问题

  • 第1题：

    在1至100这100个数中，有既不能被5整除也不能被9整除的数，它们的和是( )。

    A 1 644

    B．1779

    C．3406

    D．3541


    正确答案：D
    64．D[解析]先求出被5或9整除的数的和。
    1至100中被5整除的数有5，10，15，?，100，和为：5+10+15+?+100=(100+5)X 20÷2=1050
    1至100中被9整除的数有9，18，?，99，和为：9+18+27+?+99=(9+99)×ll÷2=594
    又因为1— 100中， 45、90这两个数同时被5与9整除， 于是所求的和是(1+2+?+
    100)一(5+10+?+100)一(9+18+?+99)+(45+90)=3541。
    因此，本题正确答案为D。

  • 第2题：

    把自然数n的各位数字之和记为Sn，如n=38，Sn=3+8-11。若对某些自然数n满足n-Sn-2007．则n的最大值是()。

    A．2010

    B．2016

    C．2019

    D．2117


    正确答案：C


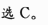
  • 第3题：

    一个四位数为完全平方数，其中个位数与十位数相同，百位和千位上的数字相同，则这个数的各位数上的数字之和为（ ）

    A、22

    B、20

    C、18

    D、16


    正确答案：A

    下面我们将c代入验证：当c=4时，100a+b=176，不合题意，不成立；当c=5时，100a+b=275，不合题意，不成立；当c=6时，100a+b=396，不合题意，不成立；当c=7时，100a+b=539，不合题意，不成立；当c=8 时，100a+b=704，满足题干要求，此时a=7，b=4；当c=9时，100a+b=891，不合题意，不成立。故c=8，a=7，b=4时成立，a+b=11。故选A。

  • 第4题：

    在1992后面补上三个数字，组成一个七位数，使它分别能被2、3、5、11整除，这个七位数最小是( )。

    A．1992330

    B．1992210

    C．1992235

    D．1992110


    正确答案：B
    12．B [解析]设这个7位数为1992abc(即为A)， 因为2 | A(A能被2整除)，5 | A，所以，c一0；
    因为3 | A，所以3 l(a-}-b)；因为ll | A，所以a-b=1。考虑到所组成的七位数应该最小， 因而取a+b=3。这就推出，a=2，b=1。即要求的最小的七位数是l992210。说明：解答本题需要熟悉能被2、5、3、11整除的数的特征，再把根据这些特征推出的结果综合在一起，加上“最小”这一条件，就可以确保答案是唯一的。

  • 第5题：

    六位数442738，能被72整除，且这六个数之和能被9整除，A与B的值为（ ）。

    A．6，5

    B．5，6

    C．7，0

    D．6，2


    正确答案：B
    72—8×9，因此六位数A42738能被8与9整除，所以后三位738能被8整除，故B=6。又由于A+4+2+7+3+B能被9整除，结合选项所以A=5。

  • 第6题：

    173□是个四位数，小明在这个□中先后填人3个数字，所得到的3个四位数，依次可被 9、11、6整除。问：小明先后填人的3个数字的和是多少？

    A.19
    B.21
    C.23
    D.17

    答案：A
    解析：
    1730分别除以9、11、6，余数为2、3、2。因此个位需要分别加上9-2=7,11-3=8，6-2=4,才能保证被9、11、6整除，则这3个数之和为7+8+4=19。

  • 第7题：

    三个数的和为252,这三个数分别能被6,7,8整除,而且商相同,则最大的数与最小的数相差

    A.18
    B.20
    C.22
    D.24
    E.26

    答案：D
    解析：
    设商为k,则这三个数为6k,7k,8k,由三个数的和为252,可得6k+7k+8k=252,解得k=12.故8k一6k=2k=24

  • 第8题：

    一个自然数的因数是指能够整除该数的自然数，超完满数指的是一个数的所有因数之和超过自身两倍的数。
    根据上述定义，以下哪项中的数是超完满数？

    A.6
    B.12
    C.16
    D.28

    答案：B
    解析：
    本题属于单定义判断。
    定义关键信息是：一个数的所有因数之和超过自身两倍。
    A项，“6”的因数有1、2、3、6，因数和为12，没有超过“6”的两倍”，不符合定义；
    B项，“12”的因数有1、2、3、4、6、12，因数和为28，超过了“12”的两倍，符合定义；
    C项，“16”的因数有1、2、4、8、16，因数和为31，没有超过“16”的两倍，不符合定义；
    D项，“28”的因数有1、2、4、7、14、28，因数和为56，没有超过“28”的两倍，不符合定义。
    因此，选择B选项。

  • 第9题：

    充分条件指的是对于两个命题X和Y，当X成立时，则Y成立，那么X是Y的充分条件；必要要条件指的是对于两个命题X和Y，当X不成立时，则Y不成立，那么X是Y的必要条件。
    根据上述定义，下列哪项中X是Y的必要条件？

    A.X：该数能被6整除；Y：该数能被2整除
    B.X：该数能被6整除；Y：该数能被4整除
    C.X：该数能被3整除；Y：该数能被6整除
    D.X：该数能被4整除；Y：该数能被3整除

    答案：C
    解析：
    本题考查“必要条件”的定义。
    其关键信息为：当X不成立时，则Y不成立。
    A项，当一个数不能被6整除时，无法得到该数不能被2整除，比如“4”，不符合定义，故A项错误，排除。
    B项，当一个数不能被6整除时，无法得到该数不能被4整除，比如“4”，不符合定义，故B项错误，排除。
    C项，因为6可以被分解为2×3，所以不能被3整除，就一定就不能被6整除，符合定义，故C项正确，当选。
    D项，当一个数不能被4整除时，无法得到该数不能被3整除，比如“6”，不符合定义，故D项错误，排除。
    故本题的正确答案为C项。

  • 第10题：

    三段论：“因为3258的各位数字之和能被3整除，所以3258能被3整除”。前提是（）

    • A、 “3258能被3整除”是小前提
    • B、 “3258的各位数字之和能被3整除”是大前提
    • C、 “各位数字之和能被3整除的数都能被3整除” 是省略的大前提
    • D、 “3258能被3整除”是大前提

    正确答案:C

  • 第11题：

    判断题
    偶数是能被2整除的数，所以 所有能被2整除的数是偶数。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第12题：

    单选题
    数据结构与算法里，完数是完美数，它等于（）
    A

    所有因子之和

    B

    只能被1和它本身整除

    C

    是该范围内最大的质数

    D

    所有小于它的数之和


    正确答案： B
    解析： 暂无解析

  • 第13题：

    设M、N都是自然数，记PM是自然数M的各位数字之和，PN是自然数N的各位数字之和。又记M*N是M除以N的余数。已知M+N=4084，那么(PM+PN)*9的值是( )。

    A．7

    B．9

    C．0

    D．5


    正确答案：A
    [答案] A。解析：特殊值法。可取M=4000,N=84，则PM+PN=16,(PM+PN)×9=7。

  • 第14题：

    某个三位数的数值是其各位数字之和的23倍。这个三位数为

    A．702

    B．306

    C．207

    D．203


    正确答案：C
    【答案】C
    【解析】选项中各位数字和，ABC三选项都为9，D为5，且203无法整除5，故排除D；用9这个约数代入，C选项是923，故选C。

  • 第15题：

    用数字4、5、6、7、8、9这六个数字组成一个六位数ABCDEF(不一定按给出数字的顺序排列)，若把A移到最后，所得的六位数BCDEFA能被2整除，若再把8移到最后，所得的六位数CDEFAB能被3整除，…，依此类推，若把E移到最后，所得的六位数能被6整除，则六位数ABCDEF的最小值为（ ）。

    A．476598

    B．476589

    C．456789

    D．465879


    正确答案：B
    此题可用排除法，因为把D移到最后，可以被5整除，所以D一定为5，排除C、D；若要保证能被2、4、6整除，所以A、C、E必须是偶数，排除A，故选B。

  • 第16题：

    有一类数，每一个数都能被11整除，并且各位数字之和是20，问这类数中，最小的数是。


    正确答案：
    1199

  • 第17题：

    有一个四位数，能被72整除，其千位与个位之和为10，个位数是为质数的偶数，去掉千位与各位得到一个新数为质数，这个四位数是多少?


    A. 8676
    B. 8712
    C. 9612
    D. 8532

    答案：B
    解析：
    解题指导： 由题目可知，个位数是2，那么千位数应是8，去掉千位和个位的新数是质数，BD都是质数，所以只能拿BD的数去除72，只有B才能被72整除。故答案为B。

  • 第18题：

    编程求出个位数字是4且能被7整除的所有3位数之和。


    答案：
    解析：



  • 第19题：

    在1至100这100个数中，有既不能被5整除也不能被9整除的数，它们的和是（ ）。
    A. 1644 B. 1779 C. 3406 D. 3541


    答案：D
    解析：
    先求出被5或9整除的数的和。
    1-100中被5整除的数有5，10，15，...，100，和为 5 + 10 + 15+-----+100=(100 + 5) X20 + 2 = 1050。
    1-100中被9整除的数有9，18，…，99，和为 9 + 18 + 27+-----+99= (9 + 99) X 11 + 2 = 594。
    又因为1-100中，45，90这两个数同时被5与9整除，于是所求的和是(1 + 2+-----+100)-(5 +10+-----+100)-(9 + 18+-----+99) +(45 + 90) = 3541。

  • 第20题：

    一个四位数为完全平方数，其中个俾数与十位数相同，百位和千位4：的数字相同，则这个数的各位数上的数字之和为（ ）。
    A. 22 B. 20 C. 18 D. 16


    答案：A
    解析：

  • 第21题：

    数据结构与算法里，完数是完美数，它等于（）

    • A、所有因子之和
    • B、只能被1和它本身整除
    • C、是该范围内最大的质数
    • D、所有小于它的数之和

    正确答案:A

  • 第22题：

    偶数是能被2整除的数，所以 所有能被2整除的数是偶数。


    正确答案:错误

  • 第23题：

    单选题
    一个四位数“□□□□”分别能被15、12和10整除，且被这三个数整除时所得的三个商的和为1365，问四位数“□□□□”中四个数字的和是多少？（　　）
    A

    17

    B

    16

    C

    15

    D

    14


    正确答案： C
    解析：
    设此数为x，由题意可知，x÷15＋x÷12＋x÷10＝1365，得x＝5460，则四个数字的和是5＋4＋6＋0＝15。

  • 第24题：

    单选题
    三段论：“因为3258的各位数字之和能被3整除，所以3258能被3整除”。前提是（）
    A

     “3258能被3整除”是小前提

    B

     “3258的各位数字之和能被3整除”是大前提

    C

     “各位数字之和能被3整除的数都能被3整除” 是省略的大前提

    D

     “3258能被3整除”是大前提


    正确答案： B
    解析： 暂无解析

相关内容