如果x*是f(x)=0的重根,则牛顿法在根x*的附近是一次收敛的,并且无法加以改进.
题目
如果x*是f(x)=0的重根,则牛顿法在根x*的附近是一次收敛的,并且无法加以改进.
相似考题
参考答案和解析
更多“如果x*是f(x)=0的重根,则牛顿法在根x*的附近是一次收敛的,并且无法加以改进.”相关问题
-
第1题:
解非线性方程f(x)=0的牛顿迭代法在重根附近()A、线性收敛
B、三次收敛
C、平方收敛
D、不收敛
参考答案:A
-
第2题:
设求方程f(x)=0的根的牛顿法收敛,则它具有()敛速。
A、超线性
B、平方
C、线性
D、三次
参考答案:C
-
第3题:
补充程序Ccon031.C,使其用牛顿迭代法求方程2x3-4x2+3x-6=0在1.5附近的根。
/**/main()/**/
}/**/while/**/(fabs(x-x0)>=1e-6); -
第4题:
设x=a是代数方程f(x)=0的根,则下列结论不正确的是( )。A、 叫是f(x)的因式
B、X-a整除f(x)
C、(a,0)是函数y=f(x)的图象与2轴的交点
D、 f(a)=0答案:D解析:由于X,=01是代数方程f(x)-0的根,故有f(a)=o,x一a是f(x)的因式.X-Ot整除f(x),(a,0) f(a)=0,比如f(x)≈x-2。
f(a)=0,比如f(x)≈x-2。 -
第5题:
用简单迭代法求方程f(x)=0的实根,把方程f(x)=0表示成x=φ(x),则f(x)=0的根是()。
- A、y=φ(x)与x轴交点的横坐标
- B、y=x与y=φ(x)交点的横坐标
- C、y=x与x轴的交点的横坐标
- D、y=x与y=φ(x)的交点
正确答案:B -
第6题:
若f(x)∈F[x],若c∈F使得f(c)=0,则称c是f(x)在F中的一个根。
正确答案:正确 -
第7题:
解非线性方程f(x)=0的牛顿迭代法具有()收敛。
正确答案:局部平方 -
第8题:
下列结论不正确的是()。
- A、y=f(x)在点x0处可微,则f(x)在点x0处连续
- B、y=f(x)在点x0处可微,则f(x)在点x0处可导
- C、y=f(x)在点x0处连续,则f(x)在点x0处可微
- D、y=f(x)在点x0处可导,则f(x)在点x0处连续
正确答案:C -
第9题:
单选题(2008)设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f′(x)>0,f″(x)>0则在(-∞,0)内必有:()Af′(x)>0,f″(x)>0
Bf′(x)<0,f″(x)>0
Cf′(x)>0,f″(x)<0
Df′(x)<0,f″(x)<0
正确答案: C解析: 暂无解析 -
第10题:
判断题若f(x)∈F[x],若c∈F使得f(c)=0,则称c是f(x)在F中的一个根。A对
B错
正确答案: 对解析: 暂无解析 -
第11题:
单选题下列说法中正确的是( )。[2014年真题]A若f′(x0)=0,则f(x0)必须是f(x)的极值
B若f(x0)是f(x)的极值,则f(x)在点x0处可导,且f′(x0)=0
C若f(x0)在点x0处可导,则f′(x0)=0是f(x)在x0取得极值的必要条件
D若f(x0)在点x0处可导,则f′(x0)=0是f(x)在x0取得极值的充分条件
正确答案: B解析:
当f(x0)在点x0处可导时,若f(x)在x0处取得极值,则可知f′(x0)=0;若f′(x0)=0,f(x)在点x0未必取得极值,例如f(x)=x3在点x=0处有f′(0)=0,但x3在实数域内不存在极值点。 -
第12题:
单选题(2013)若f(-x)=-f(x)(-∞0,f″(x)<0,则f(x)在(0,+∞)内是:()Af′(x)>0,f″(x)<0
Bf′(x)<0,f″(x)>0
Cf′(x)>0,f″(x)>0
Df′(x)<0,f″(x)<0
正确答案: C解析: 暂无解析 -
第13题:
设求方程f(x)=0的根的牛顿法收敛,则它具有()收敛。A、超线性
B、平方
C、线性
D、三次
参考答案:C
-
第14题:
设f(x)=(x-1)(x-2)(x-3),则方程f′(x)=0在(0,3)内的根的个数为(56)。
A.1
B.2
C.3
D.4
正确答案:C
解析:由罗尔定理,设函数f(x)在闭区间[a,b]上连续,在开区间(a,B)内可导,且f(A)=f(B),则在(a,B)内至少存在一点ξ使得f′ξ=0,aξb。则f(x)=x(x-1)(x-2)(x-3)在(-∞+∞)内连续且可导,又f(0)=f(1)=f(2)=f(3)=0,所以由罗尔定理可知f′(x)=0在(0,3)内至少有3个根。又f(x)是4次多项式f′(x)是3次多项式,从而f′(x)=0是3次方程,只有3个根,故答案选C。 -
第15题:
若a,6是方程f(x)=0的两个相异的实根,f(x)在[a,b]上连续,且在(a,b)内可导,则方程f´(x)=0在(a,b)内( ).A.只有一个根
B.至少有一个根
C.没有根
D.以上结论都不对答案:B解析: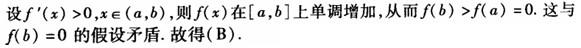
-
第16题:
用二分法求方程f(x)=x3+x-1=0在区间[0,1]内的根,进行一步后根的所在区间为(),进行两步后根的所在区间为()。
正确答案:0.5,1;0.5,0.75 -
第17题:
用牛顿切线法解方程f(x)=0,选初始值x0满足(),则它的解数列{xn}n=0,1,2,…一定收敛到方程f(x)=0的根。
- A、f(x0)f″(x)>0
- B、f(x0)f′(x)>0
- C、f(x0)f″(x)<0
- D、f(x0)f′(x)<0
正确答案:A -
第18题:
1是f(x)在域F[x]中的根的充要条件是x-1|f(x)。
正确答案:正确 -
第19题:
若a,b是方程f(x)=0的两个相异的实根,f(x)在[a,b]上连续,且在(a,b)内可导,则方程f’(x)=0在(a,b)内().
- A、只有一个根
- B、至少有一个根
- C、没有根
- D、以上结论都不对
正确答案:B -
第20题:
填空题用二分法求方程f(x)=x3+x-1=0在区间[0,1]内的根,进行一步后根的所在区间为(),进行两步后根的所在区间为()。正确答案: 0.5,1,0.5,0.75解析: 暂无解析 -
第21题:
单选题用牛顿切线法解方程f(x)=0,选初始值x0满足(),则它的解数列{xn}n=0,1,2,…一定收敛到方程f(x)=0的根。Af(x0)f″(x)>0
Bf(x0)f′(x)>0
Cf(x0)f″(x)<0
Df(x0)f′(x)<0
正确答案: A解析: 暂无解析 -
第22题:
填空题解非线性方程f(x)=0的牛顿迭代法具有()收敛。正确答案: 局部平方解析: 暂无解析 -
第23题:
单选题若f(-x)=-f(x)(-∞<x<+∞),且在(-∞,0)内f′(x)>0,f″(x)<0,则f(x)在(0,+∞)内是( )。[2013年真题]Af′(x)>0,f″(x)<0
Bf′(x)<0,f″(x)>0
Cf′(x)>0,f″(x)>0
Df′(x)<0,f″(x)<0
正确答案: C解析:
由f(-x)=-f(x)(-∞<x<+∞),知f(x)为奇函数,奇函数关于原点对称。根据奇函数图形,故在(0,+∞)内,f′(x)>0,f″(x)>0。 -
第24题:
单选题设求方程f(x)=0的根的牛顿法收敛,则它具有()敛速。A超线性
B平方
C线性
D三次
正确答案: D解析: 暂无解析
