1、设 A,B 为 n 阶可逆阵。下列说法不正确的是A．A 可经初等变换化为 B .B．A 可经初等变换化为 n 阶单位阵.C．A 不可经过初等变换化为 B 的逆矩阵.D．A 与 B 等价.

题目

1、设 A,B 为 n 阶可逆阵。下列说法不正确的是

A．A 可经初等变换化为 B .

B．A 可经初等变换化为 n 阶单位阵.

C．A 不可经过初等变换化为 B 的逆矩阵.

D．A 与 B 等价.

相似考题

1.设A、B为同阶可逆矩阵,则下列正确的说法是()。A.A+B可逆B.A-B可逆C.A+B与A-B可逆D.AB可逆

2.设A,B为n阶对称矩阵,下列结论不正确的是().A.AB为对称矩阵 B.设A,B可逆,则A^-1+B^-1为对称矩阵 C.A+B为对称矩阵 D.kA为对称矩阵

3.设A,B为n阶可逆矩阵,则().

4.设A为n阶可逆矩阵，则下面各式恒正确的是（ ）.

更多“1、设 A,B 为 n 阶可逆阵。下列说法不正确的是”相关问题

  • 第1题：

    设

    A、B都是n阶可逆矩阵，则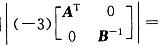

    答案：D
    解析：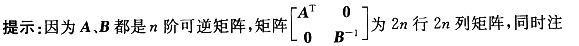

  • 第2题：

    设A为m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r1，矩阵B=AC的秩为r，则



    答案：C
    解析：

  • 第3题：

    设A，B为n阶可逆矩阵,下面各式恒正确的是( ).



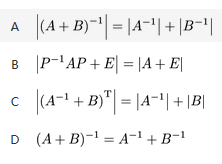    答案：B
    解析：

  • 第4题：

    设A为n阶可逆方阵，则( )不成立。

    A.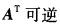
    B.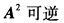
    C.-2A可逆
    D.A+E可逆

    答案：D
    解析：

  • 第5题：

    设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.


    答案：
    解析：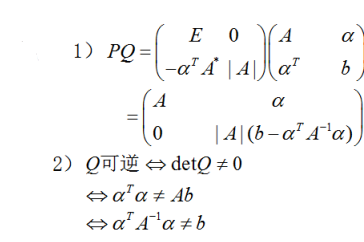

  • 第6题：

    设a为N阶可逆矩阵，则（ ）.《》（ ）


    答案：C
    解析：

  • 第7题：

    设A，B是n阶方阵，下列命题正确的是（）．

    • A、若A，B都是可逆阵，则A+B也是可逆阵
    • B、若A+B是可逆阵，则A、B中至少有一个是可逆阵
    • C、若AB不是可逆阵，则A、B也都不是可逆阵
    • D、若ATA=E，则

    正确答案:D

  • 第8题：

    设A为n阶可逆矩阵，则（-A）的伴随矩阵（-A）*等于（）。

    • A、-A*
    • B、A*
    • C、（-1）nA*
    • D、（-1）n-1A*

    正确答案:D

  • 第9题：

    设A为n阶可逆方阵，则（）不成立。

    • A、AT可逆
    • B、A2可逆
    • C、-2A可逆
    • D、A+E可逆

    正确答案:D

  • 第10题：

    单选题
    设A为n阶可逆矩阵，则（-A）的伴随矩阵（-A）*等于（）。
    A

    -A*

    B

    A*

    C

    （-1）nA*

    D

    （-1）n-1A*


    正确答案： B
    解析： 暂无解析

  • 第11题：

    设A为n阶可逆矩阵，则(-A)的伴随矩阵(-A)*等于( )。

    A.-A.*
    B.A.*
    C.(-1)nA.*
    D.(-1)n-1A.*

    答案：D
    解析：
    ∵A*=|A|A~-1 ∴(-A)*=|-A|(-A)~-1=(-1)~n|A|(-1)~-1A-1 =(-1)~n-1|A|A-1=(-1)~n-1A*

  • 第12题：

    设A为n阶矩阵,A^2=A,则下列结论成立的是().

    A.A=O
    B.A=E
    C.若A不可逆,则A=O
    D.若A可逆,则A=E

    答案：D
    解析：
    因为A^2=A，所以A(E-A)=O，由矩阵秩的性质得，r(A)+r(E—A)=n，若A可逆，则r(A)=n，所以r(E-A)=0，A=E，选(D).

  • 第13题：

    设A为n阶实对称矩阵,下列结论不正确的是().

    A.矩阵A与单位矩阵E合同
    B.矩阵A的特征值都是实数
    C.存在可逆矩阵P,使P^-1AP为对角阵
    D.存在正交阵Q,使Q^TAQ为对角阵

    答案：A
    解析：
    根据实对称矩阵的性质，显然(B)、(C)、(D)都是正确的，但实对称矩阵不一定是正定矩阵，所以A不一定与单位矩阵合同，选(A).

  • 第14题：

    设A1，A2分别为m阶，n阶可逆矩阵，分块矩阵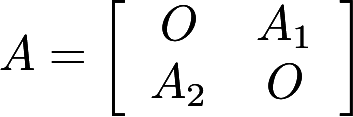.证明：A可逆，且


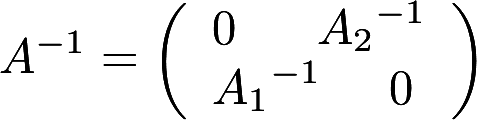    答案：
    解析：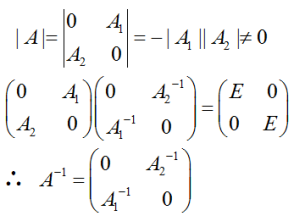

  • 第15题：

    设A为n阶非零矩阵，E为n阶单位矩阵，若A^3=O，则



    A.AE-A不可逆，E+A不可逆
    B.E-A不可逆，E+A可逆
    C.E-A可逆，E+A可逆
    D.E-A可逆，E+A不可逆

    答案：C
    解析：
    判断矩阵A可逆通常用定义，或者用充要条件行列式｜A｜≠0(当然｜A｜≠0又有很多等价的说法).因为(E-A)(E+A+A^2)=E-A^3=E，(E+A)(E-A+A^2)=E+A^3=E，所以，由定义知E-A，E+A均可逆.故选(C).

    【评注】本题用特征值也是简捷的，由A^3=O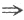A的特征值λ=0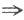E-A(或E+A)特征值均不为0｜E-A｜≠0(或｜E+A｜≠0)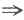E-A(或E+A)可逆

  • 第16题：

    设A为n阶可逆矩阵，则(-A)的伴随矩阵(-A)n等于（ ）。
    A. -An B. An C. (-1)nAn D. (-1)n-1An


    答案：D
    解析：
    提示：(-A)的代数余子式是由A的代数余子式乘以(-1)n-1。

  • 第17题：

    设A为4阶方阵，|A|-a≠0，则下列结论不正确的是（）。


      正确答案:D

    • 第18题：

      设A，B是n阶对称阵，Λ是对角阵，下列矩阵中不是对称阵的是（）．

      • A、A+2E
      • B、A+Λ
      • C、AB
      • D、A-B

      正确答案:C

    • 第19题：

      单选题
      设A，B是n阶方阵，下列命题正确的是（）．
      A

      若A，B都是可逆阵，则A+B也是可逆阵

      B

      若A+B是可逆阵，则A、B中至少有一个是可逆阵

      C

      若AB不是可逆阵，则A、B也都不是可逆阵

      D

      若ATA=E，则


      正确答案： D
      解析： 暂无解析

    相关内容