:有一种长方形小纸板,长为19毫米,宽为11毫米。现在用同样大小的这种小纸板拼合成一个正方形,问最少要几块这样的小纸板?( )A.157块B.172块C.209块D.以上都不对
题目
:有一种长方形小纸板,长为19毫米,宽为11毫米。现在用同样大小的这种小纸板拼合成一个正方形,问最少要几块这样的小纸板?( )
A.157块
B.172块
C.209块
D.以上都不对
相似考题
更多“:有一种长方形小纸板,长为19毫米,宽为11毫米。现在用同样大小的这种小纸板拼合成一个正方形 ”相关问题
-
第1题:
如图,由四个全等的小长方形拼成一个大正方形,每个长方形的面积都是1,且长与宽之比大于等于2,则这个大正方形的面积至少为 ()。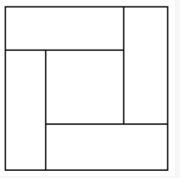 A.3
A.3
B.4.5
C.5
D.5.5答案:B解析:第一步,本题考查几何问题,属于其他几何类。
第二步,大正方形的面积=小长方形面积×4+中间小正方形的面积,由于每个长方形的面积都确定为1,那么要使大正方形的面积最小,则应使中间小正方形的面积最小。
第三步,设长方形的长为x,宽为y,则中间小正方形的边长为x-y,面积为(x-y)2,由条件可知x≥2y,那么当x=2y时,中间小正方形的面积(x-y)2最小,大正方形的面积也为最小。已知每个长方形的面积都为1,那么
第四步,大正方形的面积=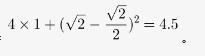
因此,选择B选项。 -
第2题:
一块正方形规划用地,计划将其分隔成若干个长为10 米,宽为7 米的小长方形地块,用以种植不同的绿植,分割数量正好为整且没有剩余土地,那么分割成的长方形地块有( )。A.50
B.70
C.80
D.35答案:B解析:分成的长方形的面积为70,原正方形的面积为完全平方数,根据选项可确定分割的长方形土地一共有70 块,选择B。 -
第3题:
一个箱子的底部由5块正方形纸板 ABCDE和1块长方形纸板F拼接而成(如图所示),已知A、B两块纸板的面积比是1:16,假设A纸板的边长为2厘米,则该箱子底部的面积为( )平方厘米。
 A.200
A.200
B.320
C.360
D.420答案:C解析:第一步,本题为几何问题。第二步,A、B面积之比是1:16,则边长之比是1:4,A的边长为2,可知B的边长为8。各线段长度标注在图形上如下:

第三步,可知整个底部的面积是(10+8)×(8+6+6)=18×20=360。因此,选择C选项。 -
第4题:
有一种长方形小纸板,长为19毫米,宽为11毫米。现在用同样大小的这种小纸板拼合成一个正方形,问最少要几块这样的小纸板?
A. 157块
B. 172块
C. 209块
D. 以上都不对答案:C解析:解题指导: 209块
11与19最小公倍数为11*19=209 -
第5题:
有一种长方形小纸板,长为29毫米,宽为11毫米。现在用同样大小的这种小纸板拼合成一个正方形,问最少要多少块这样的小纸板?( )
A.197块 B.192块 C.319块 D.299块答案:C解析:本题可转化为求29与11的最小公倍数,即为29×11=319,则组成正方形的边长为319,从而可得组成正方形的小纸板数为319×319÷(29×11)=319(块)。故正确答案为C。
