甲校与乙校学生人数比是4：5，乙校学生人数的3倍等于丙校学生人数的4倍，丙校学生人数的1／5等于丁校学生人数的1／6，又甲校女生占全校学生总数的3／8，丁校女生占全校学生总数的4／9，且丁校女生比甲校女生多50人，则四校的学生总人数为（ ）。A．1920人B．1865人C．1725人D．1640人

题目

甲校与乙校学生人数比是4：5，乙校学生人数的3倍等于丙校学生人数的4倍，丙校学生人数的1／5等于丁校学生人数的1／6，又甲校女生占全校学生总数的3／8，丁校女生占全校学生总数的4／9，且丁校女生比甲校女生多50人，则四校的学生总人数为（ ）。

A．1920人

B．1865人

C．1725人

D．1640人

相似考题

1.正、副教授人数最多的学校是（ ）。A．甲校B．乙校C．丙校D．丁校

2.甲校与乙校学生人数比是4:5，乙校学生人数的3倍等于丙校学生人数的4倍，丙校学生人数的 等于丁校学生人数的 ，又甲校女生占全校学生总数的 ，丁校女生占全校学生总数的 ，且丁校女生比甲校女生多50人，则四校的学生总人数为( )。A．1920人B．1865人C．1725人D．1640人

3.：正、副教授人数最多的学校是（ ）。A．甲校B．乙校C．丙校D．丁校

4.正、副教授人数最多的学校是（ ）。A.甲校B.乙校C.丙校D.丁校

更多“甲校与乙校学生人数比是4:5,乙校学生人数的3倍等于丙校学生人数的4倍,丙校学生人数的1／ ”相关问题

  • 第1题：

    某旅行杜拟在暑假期间面向学生推出“林州红旗渠一日游”活动，收费标准如下：

    人数m

    0＜m≤100

    100＜m≤200

    m＞200

    收费标准（元/人）

    90

    85

    75

    甲、乙两所学校计划组织本校学生自愿参加此项活动．已知甲校报名参加的学生人数多于100人，乙校报名参加的学生人数少于100人．经核算，若两校分别组团共需花费20800元，若两校联合组团只需花赞18000元．

    （1）两所学校报名参加旅游的学生人数之和超过200人吗？为什么？

    （2）两所学校报名参加旅游的学生各有多少人？


    正确答案：

    考点：二元一次方程组的应用。

    专题：方程思想。

    分析：（1）由已知分两种情况讨论，即a＞200和100a≤200，得出结论；

    （2）根据两种情况的费用，即a＞200和100a≤200分别设未知数列方程组求解，讨论得出答案．

    解答：解：（1）设两校人数之和为a．

    若a＞200，则a=18000÷75=240．

    若100a≤200，则 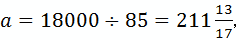 ，不合题意．

    所以这两所学校报名参加旅游的学生人数之和等于240人，超过200人．

    （2）设甲学校报名参加旅游的学生有x人，乙学校报名参加旅游的学生有y人，则

    ①当100x≤200时，得 

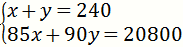
    解得 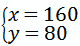 （6分）

    ②当x＞200时，得 

    解得 

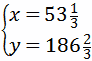
    此解不合题意，舍去．

    ∴甲学校报名参加旅游的学生有160人，乙学校报名参加旅游的学生有80人．

    点评：此题考查的是二元一次方程组的应用，关键是把不符合题意的结论舍去．

  • 第2题：

    甲校与乙校学生人数比是4∶5，乙校学生人数的3倍等于丙校学生人数的4倍，丙校学生人数的1/5等于丁校学生人数的1/6，又甲校女生占全校学生总数的3/8，丁校女生占全校学生总数的4/9，且丁校女生比甲校女生多50人，则四校的学生总人数为（ ）。

    A. 1920人
    B. 1865人
    C. 1725人
    D. 1640人

    答案：C
    解析：
    按题意，乙、丙两校人数之比是4∶3，丙、丁两校人数之比是1/6∶1/5，设丁校学生数为“1”，甲校学生数为x，于是得: x＝4×4×1/6×1/5×3×1/5=8/9 即甲、丁两校人数之比是8∶9。因甲校学生数相当于丁校的8/9，而甲校学生的3/8是女生，故甲校的女生相当于丁校学生数的8/9×3/8＝1/3。按题意，丁校学生数的4/9比1/3多50人，故丁校学生数为50÷(4/9-1/3)=450(人),甲校学生为450×8/9＝400（人），乙校学生为400×5/4＝500（人），丙校学生为500×3/4＝375（人）。故四校学生总数为400+500+450+375＝1725（人）。故答案为C。

  • 第3题：

    现有甲、乙两所学校，根据上年度的经费实际投入统计，若仅仅比较在校本科生的学生人均投入经费，甲校高于乙校的86%；但若比较所有学生（本科生加上研究生）的人均经费投入，甲校是乙校的118%。各校研究生的人均经费投入均高于本科生。根据以上信息，最可能得出以下哪项？

    A.上年度，甲校学生总数多于乙校。
    B.上年度，甲校研究生人数少于乙校。
    C.上年度，甲校研究生占该校学生的比例高于乙校。
    D.上年度，甲校研究生人均经费投入高于乙校。
    E.上年度，甲校研究生占该校学生的比例高于乙校，或者甲校研究生人均经费投入高于乙校

    答案：E
    解析：
    根据题干条件，甲乙两所院校仅比较本科生人均经费和比较所有学生人均经费的结果有较大差异，说明导致差异的原因是研究生学生在所有学生所占的比例或研究生的投入经费是不同的。如果研究生所占比例低，则所有学生的人均经费比单独计算本科生高；如果研究生投入人均经费高，也会使所有学生的人均经费比单独计算本科生高些。所以E项最可能推出。C和D不能选，根据p真推出p或q真，可知C真和D真逗可推出E真，这样就多个选项为真。

  • 第4题：

    已知甲校学生人数是乙校学生人数的40%，甲校女生人数是甲校学生人数的30%,乙校 男生人数是乙校学生人数的42%，那么，两校女生总数占两校学生总数的（ ）。



    A. 30%
    B. 50%
    C. 40%
    D. 60%

    答案：B
    解析：
    设甲校有200人，则乙校有200 ÷ 40% = 500 (人），甲校女生有 200×30% = 60(人），乙校有女生500×(1 —42%) = 290(人），两校女生共350人，两校学生共 700人，所以女生总数占50%。

  • 第5题：

    就两校的学生人数看，A、B两校都比C、D两校规模大，要断定E校的学生人数比D校的学生人数多，就需要加上条件（）。

    A.E校的学生人数比A校多
    B.A校的学生人数比B校少
    C.E校的学生人数比B校少
    D.C校的学生人数比E校少

    答案：A
    解析：
    本题考查的知识点是关系推理中的传递关系推理。传递关系推理的一般形式为：aRb，且bRc，则aRc。所以若要断定E校学生人数比D校的多，就需加上“E校学生人数比A校或B校多”的条件。

相关内容