在稳态常物性无内热源的导热过程中,可以得出与导热率(导热系数)无关的温度分布通解,t=ax+b,其具有特性为( )。A. 温度梯度与热导率成反比 B. 导热过程与材料传导性能无关 C. 热量计算也与热导率无关 D. 边界条件不受物理性质影响
题目
在稳态常物性无内热源的导热过程中,可以得出与导热率(导热系数)无关的温度分布通解,t=ax+b,其具有特性为( )。
A. 温度梯度与热导率成反比
B. 导热过程与材料传导性能无关
C. 热量计算也与热导率无关
D. 边界条件不受物理性质影响
B. 导热过程与材料传导性能无关
C. 热量计算也与热导率无关
D. 边界条件不受物理性质影响
相似考题
更多“在稳态常物性无内热源的导热过程中,可以得出与导热率(导热系数)无关的温度分布通解,t=ax+b,其具有特性为( )。 ”相关问题
-
第1题:
单层圆柱体内一维径向稳态导热过程中,无内热源,物性参数为常数,则下列说法正确的是( )。A.导热量Φ为常数
B.导热量Φ为半径的函数
C.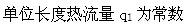
D.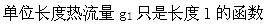 答案:C解析:
答案:C解析:
-
第2题:
如图所示,有一长圆柱,两端温度是t0,其导热系数为λ,圆柱的外柱周围是完全绝热的,圆柱内部具有热流强度为qv的均匀内热源。正确描述这圆柱内稳态温度分布的微分方程式( )。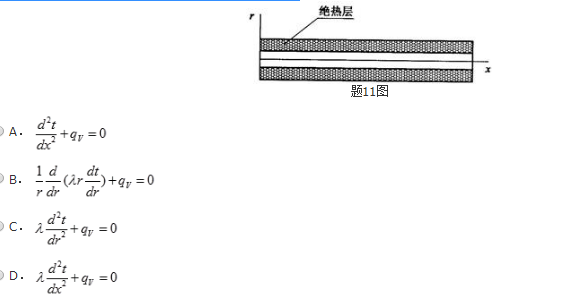 答案:B解析:
答案:B解析:
-
第3题:
单层圆柱体内径一维径向稳态导热过程中无内热源,物性参数为常数,则下列说法正确的是( )。A.Φ导热量为常数
B.Φ为半径的函数
C.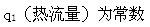
D.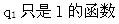 答案:C解析:Φ为圆柱体高的函数。
答案:C解析:Φ为圆柱体高的函数。 -
第4题:
某一稳态、常物性、无内热源的导热物体的表面最低温度为100℃,那么其内部绝对不可能出现的温度是()
- A、50℃
- B、200℃
- C、1000℃
- D、2000℃
正确答案:A -
第5题:
在稳态导热中,决定物体内温度分布的是()
- A、导温系数
- B、导热系数
- C、传热系数
- D、密度
正确答案:B -
第6题:
由导热微分方程可知,非稳态导热只与热扩散率有关,而与导热系数无关。你认为对吗?
正确答案: 由于描述一个导热问题的完整数学描写不仅包括控制方程,还包括定解条件。所以虽然非稳态导热的控制方程只与热扩散率有关,但边界条件中却有可能包括导热系数λ(如第二或第三类边界条件)。因此上述观点不对。 -
第7题:
对于第一类边界条件的稳态导热问题,其温度分布不导热系数有没有关系?
正确答案:寻热问题的完整数学描述包括寻热微分方程和定解条件。在寻热系数为常数的稳态寻热问题中,只有第一类边界条件下的无内热源稳态寻热问题的分析解才不寻热系数没有关系, 即寻热系数只影响热流量,而不影响温度场。 -
第8题:
绝热材料的导热系数与含水率的正确关系是:()
- A、含水率越大,导热系数越小
- B、导热系数与含水率无关
- C、含水率越小,导热系数越小
- D、含水率越小,导热系数越大
正确答案:C -
第9题:
问答题由导热微分方程可知,非稳态导热只与热扩散率有关,而与导热系数无关。你认为对吗?正确答案: 由于描述一个导热问题的完整数学描写不仅包括控制方程,还包括定解条件。所以虽然非稳态导热的控制方程只与热扩散率有关,但边界条件中却有可能包括导热系数λ(如第二或第三类边界条件)。因此上述观点不对。解析: 暂无解析 -
第10题:
问答题稳态导热时,材料内部温度的分布直线的斜率与材料的导热系数成反比,对么?为什么。正确答案: 正确的,材料的导热系数越大,热阻越小,室内外表面的温差就越小,材料内部温度的分布直线的斜率就越小(斜率=温度变化/厚度)。所以成反比。解析: 暂无解析 -
第11题:
问答题由导热微分斱程可见,非稳态导热只不热扩散率有关,而不导热系数无关。你说对吗?(提示:导热的完整数学描述为导热微分斱程和定解条件)正确答案: 上述观点不对。因为热扩散率中含有导热系数,而且导热问题的完整数学描述不仅包括控制方程,还包括定解条件,第二或第三类边界条件中都隐含着导热系数的影响。解析: 暂无解析 -
第12题:
单选题在稳态导热中,决定物体内温度分布的是()A导温系数
B导热系数
C传热系数
D密度
正确答案: A解析: 暂无解析 -
第13题:
一维大平壁内稳态无内热源导热过程中,当平壁厚度一定时,不正确的说法是( )。
A. 平壁内温度梯度处处相等
B. 材料导热率大,则壁面两侧温差小
C. 导热率与温度梯度的积为常数
D. 热流量为常数答案:A解析:根据傅里叶导热定律,一维大平壁的热流密度q的公式为:q=-λ?t/?x。式中,λ为导热率;?t/?x为温度梯度;负号表示方向。在无内热源导热过程中,热流密度q为常数,则导热率λ与温度梯度?t/?x的积为常数。当平壁厚度一定时,材料导热率λ大,温度梯度小,则壁面两侧温差小。当材料的热导率不随温度的变化而变化,平壁内温度梯度处处相等;当热导率随温度的变化而变化,平壁内温度梯度不再处处相等。 -
第14题:
物性参数为常数的一圆柱导线,通过的电流均匀发热,导线与空气间的表面传热系数为定值,建立导线的导热微分方程采用( )。A.柱坐标下一维无内热源的不稳态导热微分方程
B.柱坐标下一维无内热源的稳态导热微分方程
C.柱坐标下一维有内热源的不稳态导热微分方程
D.柱坐标下一维有内热源的稳态导热微分方程答案:D解析:圆柱导线,沿长度方向电流均匀发热,热量沿半径方向从里向外传递,因此应建立柱坐标下一维(沿半径方向)有内热源的稳态导热微分方程。 -
第15题:
在稳态、常物性、无内热源的导热物体中,最低温度出现在()
- A、内部某一点
- B、形心
- C、质心
- D、边界上
正确答案:D -
第16题:
形式为зt/зτ=a▽2.t的导热微分方程适用的范围是()
- A、非稳态导热
- B、各向异性介质
- C、导热系数随温度变化
- D、有内热源
正确答案:A -
第17题:
在稳态导热中,决定物体内部温度分布的是()
- A、导温系数
- B、导热系数
- C、传热系数
- D、体积膨胀系数
正确答案:B -
第18题:
由导热微分斱程可见,非稳态导热只不热扩散率有关,而不导热系数无关。你说对吗?(提示:导热的完整数学描述为导热微分斱程和定解条件)
正确答案:上述观点不对。因为热扩散率中含有导热系数,而且导热问题的完整数学描述不仅包括控制方程,还包括定解条件,第二或第三类边界条件中都隐含着导热系数的影响。 -
第19题:
在固体内部非稳态导热过程中,可以采用Bi和Fo准则数进行描述,其中Fo表示()
- A、热量扩散速度;
- B、导热能力大小;
- C、温度分布;
- D、边界散热特性
正确答案:A -
第20题:
单选题形式为зt/зτ=a▽2.t的导热微分方程适用的范围是()A非稳态导热
B各向异性介质
C导热系数随温度变化
D有内热源
正确答案: A解析: 暂无解析 -
第21题:
单选题在稳态常物性无内热源的导热过程中,可以得出与导热率(导热系数)无关的温度分布通解,t=ax+b,其具有特性为( )。[2018年真题]A温度梯度与热导率成反比
B导热过程与材料传导性能无关
C热量计算也与热导率无关
D边界条件不受物理性质影响
正确答案: B解析:
A项,由于gradt=(∂t/∂n)n,t=ax+b,因此温度梯度gradt与热导率λ无关。BC两项,q=-λgradt=-λ(∂t/∂n)n,因此导热过程除了与温度场有关,还与热导率λ有关。影响导热系数λ的主要因素是物质的种类和温度。D项,边界条件受外界换热环境影响,而不受物理性质的影响。 -
第22题:
问答题对于第一类边界条件的稳态导热问题,其温度分布不导热系数有没有关系?正确答案: 寻热问题的完整数学描述包括寻热微分方程和定解条件。在寻热系数为常数的稳态寻热问题中,只有第一类边界条件下的无内热源稳态寻热问题的分析解才不寻热系数没有关系, 即寻热系数只影响热流量,而不影响温度场。解析: 暂无解析 -
第23题:
单选题一维大平壁内稳态无内热源导热过程中,当平壁厚度一定时,不正确的说法是( )。[2013年真题]A平壁内温度梯度处处相等
B材料导热率大,则壁面两侧温差小
C导热率与温度梯度的积为常数
D热流量为常数
正确答案: D解析: 根据傅里叶导热定律,一维大平壁的热流密度q的公式为:q=-λ∂t/∂x。式中,λ为导热率;∂t/∂x为温度梯度;负号表示方向。在无内热源导热过程中,热流密度q为常数,则导热率λ与温度梯度∂t/∂x的积为常数。当平壁厚度一定时,材料导热率λ大,温度梯度小,则壁面两侧温差小。当材料的热导率不随温度的变化而变化,平壁内温度梯度处处相等;当热导率随温度的变化而变化,平壁内温度梯度不再处处相等。
