—个面积为1的正六边形，依次连接正六边形中点得到第二个正六边形，这样继续下去可得到第三个、第四个、第五个、第六个正六边形，问第六个正六边形的面积是多少？

题目
—个面积为1的正六边形，依次连接正六边形中点得到第二个正六边形，这样继续下去可得到第三个、第四个、第五个、第六个正六边形，问第六个正六边形的面积是多少？

相似考题

1.阐述移动通信系统正六边形无线区群的构成条件。

2.一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形面积的： A. √2 倍 B. 1.5 倍 C. √3 倍 D. 2 倍

3.一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形面积的（ ）。

4.一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形的：

更多“—个面积为1的正六边形，依次连接正六边形中点得到第二个正六边形，这样继续下去可得到第三个、第四个、第五个、第六个正六边形，问第六个正六边形的面积是多少？ ”相关问题

  • 第1题：

    一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形的：



    A.√2倍
    B.1.5倍
    C. √3倍
    D.2倍

    答案：B
    解析：
    .［解析］ 本题为几何类题目。因为正三角形和一个正六边形周长相等，又正三角形与正六边形的边的个数比为1:2，所以其边长比为2:1，正六边形可以分成6个小正三角形，边长为1的小正三角形面积：边长为2的小正三角形面积=1:4。所以正六边形面积：正三角形的面积=1×6/4=1.5。所以选B。

  • 第2题：

    已知正六边形ABCDEF的边长为a，PA为过点A而垂直于正六边形所在平面M的垂线，且PA=a，求：
    (I)点P到AB、BC、CD各边的距离；
    (II)PD与平面M所成的角．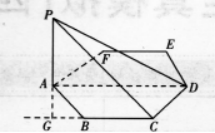


    答案：
    解析：
    (I)如图所示，
    24题答案图
    ∵PA上平面M，∴PA上BC，
    ∴点P到AB的距离为a．过A作BC的垂线交CB的延长线于G，连结PG，
    ∴BC上平面APG，即PG⊥AB，


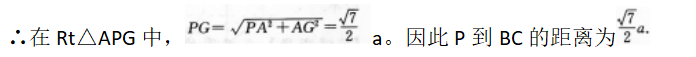
    ∵PA上平面M，
    ∴AC是PC在平面M上的射影，
    又∵AD是正六边形ABCDEF外接圆的直径，
    ∴∠ACD=90o．
    因此AC⊥CD，所以CD⊥平面ACP，即PC是P到CD的距离，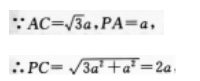

    因此P到CD的距离为2a．
    (Ⅱ)设PD与DA所夹的角为口，在Rt△PAD中，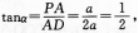

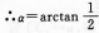    (VI)为PD与平面M所夹的角．

  • 第3题：

    图形对称性从高到低排序正确的是（）

    • A、圆形，正三角形，正方形、正六边形
    • B、圆形，正六边形、正方形、正三角形
    • C、圆形，正方形、正六边形、正三角形
    • D、圆形，正方形、正三角形，正六边形

    正确答案:B

  • 第4题：

    蜂窝式电捕焦油器的沉淀极管为（）。

    • A、正四边形
    • B、正六边形
    • C、圆形

    正确答案:B

  • 第5题：

    当试件截面积相同时，截面形状为圆形、方形和正六边形的试件，在相同试验条件下， 其试验测得的单轴抗压强度的大小关系最可能是（）

    • A、圆形>方形>正六边形
    • B、圆形<方形<正六边形
    • C、圆形>正六边形>方形
    • D、方形<圆形<正六边形

    正确答案:C

  • 第6题：

    对于面状服务区域来说，为什么说正六边形是最佳的小区形状？


    正确答案: ①在覆盖同样大小的区域时，采用正六边形小区结构所需要的小区数目最少，即所需要的基站数目最少，因而最经济；
    ②采用正六边形小区，相邻小区之间的邻频道干扰最小；
    ③在同频道载干比指标相同的情况下，采用正六边形小区所需要的最小不同频道组数最小。

  • 第7题：

    蜂窝式移动通信网由（）。

    • A、正六边形覆盖成大区制带状网。
    • B、正六边形覆盖成小区制面状网。
    • C、正六边形覆盖成大区制面状网。
    • D、正六边形覆盖成小区制带状网。

    正确答案:B

  • 第8题：

    为什么说最佳的小区形状是正六边形？


    正确答案: 对于同样大小的服务区域，采用正六边形构成的小区所需的小区数最少，故所需频率组数也最少。所以说最佳的小区形状是正六边形。

  • 第9题：

    问答题
    正六边形的放样方法是什么？

    正确答案： 在设计时只要给出正六边形的中心点的坐标，一条边和长度和方向，即可使用极坐标法放样出全部轴线点。
    解析： 暂无解析

  • 第10题：

    单选题
    蜂窝式移动通信网由（）。
    A

    正六边形覆盖成大区制带状网。

    B

    正六边形覆盖成小区制面状网。

    C

    正六边形覆盖成大区制面状网。

    D

    正六边形覆盖成小区制带状网。


    正确答案： C
    解析： 暂无解析

  • 第11题：

    问答题
    为什么说最佳的小区形状是正六边形？

    正确答案： 对于同样大小的服务区域，采用正六边形构成的小区所需的小区数最少，故所需频率组数也最少。所以说最佳的小区形状是正六边形。
    解析： 暂无解析

  • 第12题：

    问答题
    威慑呢蜂窝网要采用正六边形？

    正确答案： 在服务区面积一定的情况下，与正三角形，正方形相比，正六边形的小区最接近理想的圆形辐射模式，覆盖面积最大，他们之间的重叠面积最小，可用最少数目的小区就能覆盖整个地理区域，因此用正六边形覆盖整个服务区所需要的基站数最少，无线频率个数最少。
    解析： 暂无解析

  • 第13题：

    一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形的;


    A. 0.5倍
    B. l.5倍
    C. 1倍
    D. 2倍

    答案：B
    解析：
    解题指导： 本题为几何类题目。因为正三角形和一个正六边形周长相等，又正三角形与正六边形的边的个数比为1:2，所以其边长比为2:1，正六边形可以分成6个小正三角形，边长为1的小正三角形面积：边长为2的小正三角形面积=1:4。所以正六边形面积：正三角形的面积=1×6/4=1.5。故答案为B。

  • 第14题：

    如图所示，等边三角形的面积为45，内部有一个正六边形，问这个正六边形的面积最大为多少。



    A. 25
    B. 30
    C. 35
    D. 40


    答案：B
    解析：
    本题考查几何问题。六边形可分割成6个小的等边三角形，并且与其他三个白三角大小相同。则正六边形的面积为45÷9×6=30。因此，本题答案为B选项。

  • 第15题：

    七点法面积井网呈等边三角形，注水井按一定的井距布置在正六边形的（），呈正六边形，３口采油井分别布置在三角形的3个顶点上，采油井位于注水井所形成的正六边形的中心。

    • A、边线
    • B、腰线
    • C、中心
    • D、顶点

    正确答案:D

  • 第16题：

    正六边形的边长为10mm，求其对顶长度及对方宽度各是多少？


    正确答案: 对顶长度为＝2×边长＝2×10＝20（mm）
    对方宽度＝2×10×sin60°＝17.3（mm）
    答：边长为10mm的正六边形的对顶长度为20mm，其对方宽度为17.3mm。

  • 第17题：

    在面状覆盖的服务区中，通常采用（）的小区形状。

    • A、正方形
    • B、圆形
    • C、正六边形
    • D、正三角

    正确答案:C

  • 第18题：

    网络拓扑结构设计过程中搭建网络拓朴结构时，每个站点要用一个正六边形来表示，要求正六边形的边长是覆盖半径的（）倍


    正确答案:√3/2

  • 第19题：

    小区的形状为什么选择正六边形？


    正确答案: 在服务面积一定的情况下，正六边形小区的形状最接近理想的圆形，用它覆盖所需基站最少，也最经济。正六边形构成的网络形同蜂窝，因此称为蜂窝网

  • 第20题：

    问答题
    为何说最佳的小区形状是正六边形？

    正确答案： 小区形状的设计要求：小区无空隙、无重叠的覆盖整个服务区域。
    全向天线辐射的覆盖区为圆形，不能无空隙、无重叠的覆盖整个区域。在考虑交叠之后，实际上每个辐射区的有效覆盖区是一个多边形。满足无空隙、无重叠条件的小区形状有三种：正三角形、正方形和正六边形。而在服务区面积一定的情况下，正六边形小区的形状最接近理想的圆形，用它覆盖整个服务区所需的基站数最少，也就最经济。
    解析： 暂无解析

  • 第21题：

    单选题
    图形对称性从高到低排序正确的是（）
    A

    圆形，正三角形，正方形、正六边形

    B

    圆形，正六边形、正方形、正三角形

    C

    圆形，正方形、正六边形、正三角形

    D

    圆形，正方形、正三角形，正六边形


    正确答案： B
    解析： 暂无解析

  • 第22题：

    填空题
    网络拓扑结构设计过程中搭建网络拓朴结构时，每个站点要用一个正六边形来表示，要求正六边形的边长是覆盖半径的（）倍

    正确答案： √3/2
    解析： 暂无解析

  • 第23题：

    单选题
    一个正三角形和一个正六边形周长相等,则正六边形面积为正三角形的（ ）.
    A

    根号2倍

    B

    1.5倍

    C

    根号3倍

    D

    2倍


    正确答案： A
    解析：

相关内容