甲、乙、丙、丁四人做纸花,已知甲、乙、丙三人平均每人做了37朵,乙、丙、丁三人平均每人做了39朵,已知丁做了41朵,问甲做了多少朵? A. 35 朵 B. 36 朵 C. 37 朵 D. 39 朵
题目
B. 36 朵
C. 37 朵
D. 39 朵
相似考题
参考答案和解析
更多“甲、乙、丙、丁四人做纸花,已知甲、乙、丙三人平均每人做了37朵,乙、丙、丁三人平均每人做了39朵,已知丁做了41朵,问甲做了多少朵? ”相关问题
-
第1题:
甲、乙、丙、丁四个工人做了270个零件,如果甲多做10个,乙少做10个,丙做的个数乘2,丁做的个数除以2,那么四人做的零件数恰好相等。丙实际做多少个?( )
A.30
B.45
C.52
D 63
正确答案:A
设四人做的零件数恰好相等的数为X,则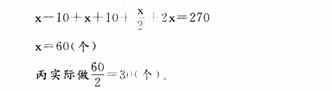
-
第2题:
甲、乙、丙、丁四人共同做一批纸盒,甲做的纸盒数是另外三人做的总和的一半,乙做的纸盒数是另外三人做的总和的1/3,丙做的纸盒数是另外三人做的总和的1/4,丁一共做了l69个,则甲一共做了( )纸盒。
A.780个 B.450个 C.390个 D.260个
正确答案:D不必列方程,分析题意可知:甲、乙、丙分别做了总纸盒数的1/3,1/4和1/5。那么总纸盒数是l69÷(1—1/3—1/4—1/5)=780个,甲一共做了260个。
-
第3题:
甲、乙、丙、丁四人共同做一批纸盒,甲做的纸盒是另外三人做的总和的一半,乙做的纸盒数是另外三人做的总和的1/3,丙的纸盒数是另外三人做的总和的1/4,丁一共做了169个,问甲一共做了多少个纸盒?( )
A.780个
B.450个
C.390个
D.260个
正确答案:D
设甲、乙、丙、丁分别做了a、b c、d,则a=(b+c+d)/2,可得a=(a+b+c+d)/3,同理可得b=(a+b+c+d)/4。即甲、乙、丙、丁分别做了总数的1/3、1/4,1/5则丁做了总数的1-1/3-1/4-1/5,所以甲做的个数为了1/3×(169÷13/60)=1/5。故正确答案为D。 -
第4题:
甲、乙、丙、丁四人共做了270道题。如果甲多做10道,乙少做10道,丙做的道数乘以2,丁做的道数除以2,那么这四个人做的题目数就恰好相等。问甲实际做了多少道题?()
A.70
B.60
C.50
D.40
正确答案:C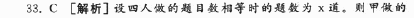

-
第5题:
甲、乙、丙、丁四人做纸花,已知甲、乙、丙三人平均每人做了37朵,乙、丙、丁三人平均每人做了39朵,已知丁做了41朵,问甲做了多少朵?A. 35 朵
B. 36 朵
C. 37 朵
D. 39 朵答案:A解析:假设法,丁为41,乙、丙、丁平均为39,那么假设丙为39,则乙为37,甲、乙、丙平均数为37,那么甲只能为35。故答案为A。 -
第6题:
甲、乙、丙、丁四人是好朋友。在某次数学考试中,甲得分最高,丁得分最低。乙、丙、丁三人的平均成绩是70,甲、乙、丙三人的平均成绩是80,甲与丁的成绩总和是156。则四人的平均成绩是( )。A. 75. 25
B. 72.75
C. 75. 75
D. 72. 75答案:C解析:分析题干可知,乙、丙、丁三人的总成绩为70×3,甲、乙、丙三人的总成绩为80×3,甲、丁二人的总成绩为156,故70×3 + 80×3 + 156等于四人总成绩的2倍。因此,四人的平均成绩是(70×3 + 80×3 + 156)÷2 + 4 = 75. 75。 -
第7题:
已知甲、乙、丙、丁四人具有以下直系、旁系血亲关系:甲是乙的父亲,丙是甲的弟弟,丁是丙的母亲。则甲、乙、丙、丁四人中年龄最大的是( )A. 甲
B. 乙
C. 丙
D. 丁答案:D解析:本题要找年龄最大的,甲是乙的父亲得知 甲>乙,所以乙不能是年龄最大,排除B;丙是甲的弟弟,说明 甲>丙,排除丙,而且甲、丙属于同辈份的。丁是丙的母亲,说明丁是甲丙的长辈,年龄肯定>甲,所以选D。 -
第8题:
已知有甲、乙、丙、丁四个数,甲、乙之和大于丙、丁之和,甲、丁之和大于乙、丙之和,乙、丁之和大于甲、丙之和。根根据以上请判断这四个数谁最小?()
A 甲最小
B 丙最小
C 乙最小
D 丁最小答案:B解析:第一步:整理题干信息。
(1)甲+乙>丙+丁;(2)甲+丁>乙+丙;(3)乙+丁>甲+丙。
第二步:根据信息整合。
将不等式相加,同方向的不等号不变,(1)+(2)可得甲>丙,(2)+(3)可得丁>丙,(1)+(3)可得乙>丙,综合三个结果可知丙最小。
故正确答案为B。 -
第9题:
甲、乙、丙、丁四人进行围棋比赛,每人都要与其他三人各赛一盘。比赛在两张棋盘上同时进行,每天每人只赛一盘。第一天甲与丙比赛,第二天丙与丁比赛,第三天乙与 比赛。A.甲
B.乙
C.丙
D.丁答案:C解析:第一步,确定题型。
题干有明显的信息匹配特征,确定为分析推理。
第二步,分析条件,进行推理。
根据题干信息特征,首先采用最大信息法,从丙的比赛情况入手,由“第一天甲与丙比赛,第二天丙与丁比赛”,又“每天每人只赛一盘”,可知,丙已经和甲、丁比完赛了,因此唯一剩下的对手就是乙,因此第三天丙要与乙比赛。 -
第10题:
甲、乙、丙三人合伙经营,后甲因急事用钱,要将自己在合伙中的份额转让,乙和第三人丁均欲以同一价格购买,甲应该()。
- A、卖给乙
- B、卖给丁
- C、卖给乙或丁
- D、卖给乙、丁每人一半份额
正确答案:A -
第11题:
一件事难坏了领导,一直不知道是谁做的,下面的事实成立,你猜猜谁做了这件事? (1)甲、乙、丙中至少有一个人做了这件事; (2)甲做了这件事,乙、丙也做了; (3)丙做了这件事,甲、乙也做了: (4)乙做了这件事,没有其他人做这件事; (5)甲、丙中至少一人做了这件事。
正确答案: 由条件2、3、5知道甲、丙不能做这件事;由条件1知道甲乙丙至少有一人做了这件事,那么乙一定做了;由条件4得,只有乙一个有罪。 -
第12题:
单选题甲、乙、丙、丁四人做纸花,已知甲、乙、丙三人平均每人做了37朵,乙、丙、丁三人平均每人做了39朵,已知丁做了41朵,问甲做了多少朵()A35
B36
C37
D39
正确答案: A解析: 甲、乙、丙三人一共做了37×3=111朵,乙、丙、丁三人一共做了39×3=117朵,则丁比甲多做了117-111=6朵花,故甲做了41-6=35朵。 -
第13题:
甲、乙、丙、TNX共做T 270道题。如果甲多做l0道,乙少做10道,丙做的道数乘以2,丁做的道数除以2,那么这四个人做的题目数就恰好相等。问甲实际做了多少道题?( )
A.70
B.60
C.50
D 40
正确答案:C
34. C[解析]设四人做的题目数相等时的题数为x道。则甲做的题数为(x一10)道, 乙
做的题数为(X+10)道,丙做的题数为x÷2=0.5x道,丁做的题数为2x道。
他们四人共做的题数为270道,则可得:
(X--10)+(X+10)+0.5x+2x=270,解得x=60。
故甲实际傲的题数为60一10=50(道)。 -
第14题:
甲乙丙丁四个人工做了270个零件,如果甲多做10个,乙少做10个,丙做的个数乘2,丁做的个数除以2,那么四人做的零件数恰好相等。丙实际做了多少个?( )
A.30 B.45 C. 52 D.63
正确答案:A
-
第15题:
甲、乙、丙、丁四人共做零件325个。如果甲多做10个,乙少做5个,丙做的个数乘以2,丁做的个数除以3,那么,四个人做的零件数恰好相等。问:丁做了多少个?( )
A.180
B.158
C.175
D.164
正确答案:A
52.【答案】A。丁做的个数可以被3整除,只有A符合题意,故选A。 -
第16题:
甲乙丙丁人中有2人在节假日为社区做好事,班主任把这4人找来了解情况4人分别回答如下: 甲:丙、丁两人中有人做了好事乙:丙做了好事,我没有 丙:甲、丁中只有一人做了好事丁:乙说的是事实 最后经调查分析,发现4人中有2人说的是事实,另外2人说的与事实有出入到底谁做了好事()?
A.甲、乙
B.丙、丁
C.甲、丙
D.乙、丁
正确答案:D
-
第17题:
甲、乙、丙、丁四人共做零件325个。如果甲多做10个,乙少做5个,丙做的个数乘以2,丁做的个数除以3,那么,四个人做的零件数恰好相等。问:丁做了多少个?( )A. 180
B. 158
C. 175
D. 164答案:A解析:由题意知,丁做的个数可以被3整除,只有A想满足。故答案为A。 -
第18题:
有甲、乙、丙、丁、四个数字,已知甲的8%为9,乙的9%为10,丙的10%为11,丁的11%为12, 则min(甲、乙、丙、丁)是:
A. 甲
B. 乙
C. 丙
D. 丁答案:D解析:解题指导: 根据题干,甲=9×100÷8=(1+1÷8)×100,乙=10×100÷9=(1+1÷9)×100,丙=11×100÷10=(1+1÷10)×100,丁=12×100÷11=(1+1÷11)×100。故答案为D。 -
第19题:
甲、乙、丙、丁四人做手工盒,已知甲、乙、丙三人平均每人做了28 个,乙、丙、丁三人平均每人做了 31 朵,已知丁做了 33 朵,问甲做了多少个?
A. 24个
B. 26个
C. 27个
D. 28个答案:A解析:解题指导: 根据题干可知,甲乙丙共做了84个,乙丙丁共做了93个,则丁-甲=9个,甲=24个。故答案为A。 -
第20题:
甲、乙、丙、丁四人做纸花,已知甲、乙、丙三人平均每人做了 37 朵,乙、丙、丁三 人平均每人做了 39 朵,已知丁做了 41 朵,问甲做了多少朵?
A.35 朵 B、36 朵 C.37 朵 D.38 朵答案:A解析:由甲、乙、丙平均做37朵,而乙、丙、丁平均做39朵,可知丁比甲多做(39-37)×3=6朵,因此甲做了41-6=35朵。故选A。 -
第21题:
甲、乙、丙、丁四人是好朋友。在某次数学考试中,甲得分最高,丁得分最低。乙、丙、丁三 人的平均成绩是70,甲、乙、丙三人的平均成绩是80,甲与丁的成绩总和是156。则四人的 平均成绩是( )。
A. 75.25 B. 72.75 C. 75.75 D. 72.75答案:C解析:C [解析】分析题干可知,乙、丙、丁三人的总成绩为70×3,甲、乙、丙三人的总成绩 为80×3,甲、丁二人的总成绩为156,故70×3 + 80×3 + 156等于四人总成绩的2倍。因此, 四人的平均成绩是(70×3+80×3 + 156)÷2÷4 = 75. 75。 -
第22题:
已知甲、乙、丙、丁四人具有以下直系、旁系血亲关系:甲是乙的父亲,丙是甲的弟弟,丁是丙的母亲。则甲、乙、丙、丁四人中年龄最大的是()。
- A、甲
- B、乙
- C、丙
- D、丁
正确答案:D -
第23题:
甲、乙、丙三人向不相识的丁某要20块钱买烟抽,遭到丁某的拒绝。甲、乙、丙三人即对丁某进行殴打,致丁某轻微伤。在三人将要离去时,甲某仍觉得不解气,又回身持刀朝丁某腿部扎了两刀,致丁某失血过多死亡。甲、乙、丙三人当如何处理?()
- A、甲、乙、丙三人构成抢劫罪和故意伤害罪
- B、甲、乙、丙三人构成寻衅滋事罪
- C、甲、乙、丙三人构成故意伤害罪
- D、甲构成故意伤害罪,乙、丙构成寻衅滋事罪
正确答案:D -
第24题:
问答题一件事难坏了领导,一直不知道是谁做的,下面的事实成立,你猜猜谁做了这件事? (1)甲、乙、丙中至少有一个人做了这件事; (2)甲做了这件事,乙、丙也做了; (3)丙做了这件事,甲、乙也做了: (4)乙做了这件事,没有其他人做这件事; (5)甲、丙中至少一人做了这件事。正确答案: 由条件2、3、5知道甲、丙不能做这件事;由条件1知道甲乙丙至少有一人做了这件事,那么乙一定做了;由条件4得,只有乙一个有罪。解析: 暂无解析
