机关运动会上,来自3个单位的参赛者正好站成1×1、2×2到9×9共9个方阵,且每个方阵的人都来自同一个单位。已知来自甲单位的人组成了1个方阵,来自乙单位的人组成了6个方阵,且乙单位的参赛者正好是丙单位的2倍。则乙单位有多少名参赛者?A.108 B.136 C.166 D.184
题目
机关运动会上,来自3个单位的参赛者正好站成1×1、2×2到9×9共9个方阵,且每个方阵的人都来自同一个单位。已知来自甲单位的人组成了1个方阵,来自乙单位的人组成了6个方阵,且乙单位的参赛者正好是丙单位的2倍。则乙单位有多少名参赛者?
A.108
B.136
C.166
D.184
B.136
C.166
D.184
相似考题
更多“ 机关运动会上,来自3个单位的参赛者正好站成1×1、2×2到9×9共9个方阵,且每个方阵的人都来自同一个单位。已知来自甲单位的人组成了1个方阵,来自乙单位的人组成了6个方阵,且乙单位的参赛者正好是丙单位的2倍。则乙单位有多少名参赛者?”相关问题
-
第1题:
某单位男女员工的人数之比是15∶13。按人数之比5∶7∶8,分为甲、乙、丙三个科室。其中甲科室男女员工的人数之比为4∶3,乙科室为5∶2。则丙科室男女员工人数之比为:A.1∶2
B.2∶3
C.5∶9
D.5∶8答案:C解析:第一步,本题考查基础应用题,用赋值法解题。
第二步,根据男女比为15∶13,则总人数应该为28的倍数;又因为甲∶乙∶丙=5∶7∶8,则总人数应该为20的倍数;所以赋值总人数为140,则男生人数为75,女生人数为65。甲=35,乙=49,丙=56。又因为甲科室的男女比为4∶3,则甲的男生为20,甲的女生为15,又因为乙科室的男女比为5∶2,则乙的男生为35,乙的女生为14,所以得出丙的男生为75-20-35=20,丙的女生为65-15-14=36,则丙的男女比=20∶36=5∶9。 -
第2题:
某调查队男、女队员的人数比是3 : 2,分别为甲、乙、丙三个调查小组。已知甲、乙、丙三组的人数比是10 : 8 : 7,甲组中男、女队员的人数比是3 : 1,乙组中男、女队员的人数比是5 : 3,则丙组中男、女 队员的人数比是( )。A. 4 : 9
B. 5 : 9
C. 4 : 7
D. 5 : 7答案:B解析:设甲、乙、丙三组人数分别为a,b,c,总人数为(a+b+c),丙组男、女队员人数比为m:n。则有:a:b:c=10:8:7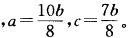
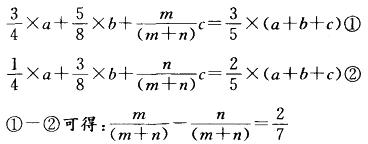
带入选项,只有B项符合要求。 -
第3题:
某单位组织员工做工间操,员工站成一个实心方阵(正方形队列)时,还多8 人,如果站成一个每边比前面多1 人的实心方阵,则还少17 人。问该单位有员工多少人?( )。A.136 人
B.152 人
C.159 人
D.177 人答案:B解析:设原方阵每边有x 人,则新方阵每边有x+1 人,由题意,2(x+1)-2x=25,解得x=12。所以共有144+8=152 人。 -
第4题:
某单位有不到100人参加远足活动,如将该单位人员平均分成N组(N>1且每组人数>1),则每组的人数有且仅有6种不同的可能性。则该单位参加活动的人数可能的最小值和最大值之间相差多少人?《》( )A.32
B.48
C.56
D.64答案:D解析:每组的人数有且仅有6种不同的可能性,说明此数字除了1和本身,有且仅有6个因子。除了1,最小的三个数是2、3、4,而2X3X4=24, 24除了能被1和24整除外,还可以被2, 3,4, 6, 8, 12整除,满足要
求,故人数可能的最小值是24人。现要使最大值最大,则其差值也应最大,故从最大值开始代入验算。D项:假设差值为64,则最大值为24+64=88, 88=2x44=4X22=8X11,刚好每组的人数有且仅有2、4、8、11、22、44 这六种不同的可能性,满足条件。 -
第5题:
某建设工程由甲、乙、丙、丁4个单位工程组成,甲单位工程最先开工;甲单位工程开工后1个月乙单位工程开工;甲单位工程开工后2个月丙、丁单位工程同时开工,则该建设工程开工报审表的正确填报方式是()。A:甲、乙2个单位工程分别填报,丙、丁2个单位工程统一填报
B:甲单位工程单独填报,乙、丙、丁3个单位工程统一填报
C:甲、乙2个单位工程统一填报,丙、丁2个单位工程统一填报
D:甲、乙、丙、丁4个单位工程统一填报答案:A解析:本题考查的是监理工作的基本表式。整个项目一次开工,只填报一次,如工程项目中涉及多个单位工程且开工时间不同,则每个单位工程开工都应填报一次。(本知识点新教材已经删除) -
第6题:
某单位每年都组织春季植树活动,今年单位把人员分成甲、乙两队分次植树,计划把树种成正方形实心方阵,第一次每队种10棵,第二次每队又种10棵,这样一直种下去,最后一次甲队仍种10棵,而乙队种的不足10棵,两队共种了二百多棵树,那么乙队最后一次种了几棵树?A.4
B.5
C.6
D.9答案:C解析:正方形实心方阵的总数=最外层每边的平方,200~300的平方数有152、225、162=256、172=289。甲、乙两队每次共种树20棵,最后一次共种了十几棵,所以方阵总数是一个十位为奇数的平方数。符合条件的只有256,所以乙队最后一次种了6棵树。 -
第7题:
甲单位接受乙单位的委托单独设计完成了某项发明创造,甲乙两单位之间并未签订其他协议,那么申请专利的权力属于__(1)__,申请被批准后,专利权归__(2)__所有或持有。空白(2)处应选择()
- A、乙单位
- B、甲和乙两单位共同
- C、甲单位
- D、其他
正确答案:C -
第8题:
某商品市场上有甲、乙两个生产厂家,甲厂生产每个商品需人工5个单位、资本1个单位,而乙厂则只需人工1个单位、资本2个单位。由此可得结论:乙厂的生产效率与效益要比甲厂的高
正确答案:错误 -
第9题:
单选题设A为n阶方阵,E为n阶单位矩阵,且A2=A,则(A-2E)-1=( )。A(A+E)/2
B-(A+E)/2
C(A-E)/2
D-(A-E)/2
正确答案: C解析:
由题设A2=A有,A2-A-2E=(A-2E)(A+E)=-2E,即(A-2E)[-(A+E)/2]=E,所以有(A-2E)-1=-(A+E)/2。 -
第10题:
单选题甲单位接受乙单位的委托单独设计完成了某项发明创造,甲乙两单位之间并未签订其他协议,那么申请专利的权力属于__(1)__,申请被批准后,专利权归__(2)__所有或持有。空白(1)处应选择()A甲和乙两单位共同所有
B甲单位
C乙单位
D其他
正确答案: D解析: 暂无解析 -
第11题:
单选题甲单位接受乙单位的委托单独设计完成了某项发明创造,甲乙两单位之间并未签订其他协议,那么申请专利的权力属于__(1)__,申请被批准后,专利权归__(2)__所有或持有。空白(2)处应选择()A乙单位
B甲和乙两单位共同
C甲单位
D其他
正确答案: B解析: 暂无解析 -
第12题:
单选题设A为n阶方阵,E为n阶单位矩阵,且A2=A,则(A-2E)-1=( )。AA+2E
BA+E
C(A+E)/2
D-(A+E)/2
正确答案: A解析:
由题设A2=A有,A2-A-2E=(A-2E)(A+E)=-2E,即(A-2E)[-(A+E)/2]=E,所以有(A-2E)-1=-(A+E)/2。 -
第13题:
甲、乙两个单位分别有60和42名职工,共同成立A、B两个业余活动小组,所有职工每人至少参加1个。乙单位职工中仅参加A组的人数是只参加一个小组人数的60%,乙单位职工中参加B组的人数与参加A组的人数之比为3∶4,参加B组的人中,甲单位职工占5/8。问有多少人仅参加A组?A.35
B.42
C.46
D.56答案:C解析:第一步,本题考查容斥问题。
第二步,设乙单位只参加一个小组的人数为5x,则只参加A组的有5x·60%=3x名职工,那么只参加B组的有5x-3x=2x名职工,设乙单位AB组都参加的有y人。可列方程:(2x+y)∶(3x+y)=3∶4,解得x=y,那么乙单位中参加B组的有3x人,参加A组的有4x人,AB都参加的有x人,可列方程:3x+4x-x=42,解得x=7,那么参加B组的有21人,只参加A组的有21人。
那么甲单位只参加A组的有60-35=25(人),那么两个单位只参加A组的有21+25=46(人)。 -
第14题:
在某次国际会议上,每国有1-2名代表参会,参会代表没有多重国籍的人。其中,甲、乙、丙和丁四人分别来自英国、德国和美国3个国家。已知:
(1)甲、乙至少有1人来自英国;
(2)乙、丙至少有1人来自德国。
如果甲、丙、丁至少有2人来自英美两国,则下列哪项是不可能的?A.甲来自德国
B.乙来自德国
C.丙来自英国
D.丁来自英国答案:A解析:第一步,确定题型。
题干有信息匹配特征,确定为分析推理。
第二步,分析条件,进行推理。
①甲、乙至少有1人来自英国
②乙、丙至少有1人来自德国
③甲、丙、丁至少有2人来自英美两国
本题可采用代入法,逐一分析选项。
A项:甲来自德国,根据①可得:乙来自英国,又根据②可得:丙来自德国,甲、丙都来自德国,不符合③甲、丙、丁至少有2人来自英美两国,所以不能推出;
B项:乙来自德国,根据①可得:甲来自英国,但是丙和丁的国籍不确定,甲、丙、丁至少有2人来自英美两国可能成立,可以推出;
C项:丙来自英国,根据②可得:乙来自德国,又根据①可得,甲来自英国,那么丁来自美国,符合③甲、丙、丁至少有2人来自英美两国,可以推出;
D项:丁来自英国,根据③可得:甲和丙至少有一个来自英美两国,与题干①②不矛盾,可以推出。
因此,选择A选项。 -
第15题:
甲、乙、丙三个单位各派2名志愿者参加公益活动,现将这6人随机分成3组,每组2人,则每组成员均来自不同单位的概率是:A.2/3
B.5/12
C.7/4
D.8/15答案:D解析:6个人随机分成3组,总数为C26×C24/A33=15种情况。每组成员来自不同的单位,正向考虑情况数较多,故反向考虑,即考虑每组成员来自相同的单位。
第一类情况:只有一组来自同一单位。设甲1甲2同一单位,则剩下的两组可能有两种情况:乙1丙1和乙2丙2;乙1丙2和乙2丙1。满足的情况数为3×2=6种。
第二类情况:有两组来自同一单位,而剩下一组也一定来自同一单位,即三组均来自同一单位,共1种情况。
则满足每组成员来自相同单位的概率=6+1/15=7/15,所求每组成员均来自不同单位的概率P=1-7/15=8/15。
故正确答案为D。 -
第16题:
某次运动会需组织长宽相等的方阵。组织方安排了一个鲜花方阵和一个彩旗方阵,两个方阵分别入场完毕后又合成一个方阵,鲜花方阵的人恰好组成新方阵的最外圈。已知彩旗方阵比鲜花方阵多28人,则新方阵的总人数为( )。A.100
B.144
C.196
D.256答案:A解析:第一步,本题考查方阵问题,用代入排除法解题。
第二步,代入A选项,即总人数为100人,根据公式总数=最外层每边人数2,可得最外层每边人数为10人,又根据最外层人数=4×最外层每边人数-4,可得最外层人数=4×10-4=36(人),即鲜花方阵的人数为36人,可得彩旗方阵的人数=100-36=64(人),两者差64-36=28(人),且36、64均为平方数,可构成方阵,满足题意。
因此,选择A选项。 -
第17题:
某建设工程由甲.乙.丙.丁4个单位工程组成,甲单位工程最先开工:甲单位工程开工后1个月乙单位工程开工;甲单位工程开工后2个月丙.丁单位工程同时开工。则该建设工程开工报审表的正确填报方式是( )。A.甲.乙2个单位工程分别填报,丙.丁2个单位工程统一填报
B.甲单位工程单独填报,乙.丙.丁3个单位工程统一填报
C.甲.乙2个甲位工程统一填报,丙.丁2个单位工程统一填报
D.甲.乙.丙.丁4个单位工程统一填报答案:A解析: -
第18题:
以如下图的圆形广场上举办一个市民文艺活动,参加活动的n名市民排成如图中的ABCD的菱形方阵(图中数字单位为米)。已知方阵面积为m平方米,且n=2m,问n的值为:
 A.92
A.92
B.120
C.192
D.240答案:C解析:
-
第19题:
甲、乙两单位签订了建设工程合同,但甲单位因丙单位的原因使合同延迟履行,则()。
- A、甲单位应向乙单位承担违约责任
- B、丙单位应向乙单位承担违约责任
- C、甲、乙单位均可向丙单位提出索赔
- D、乙单位无权解除合同
正确答案:A -
第20题:
254个志愿者来自不同的单位,任意两个单位的志愿者人数之和不少于20人,且任意两个单位志愿者的人数不同,问这些志愿者所属的单位数最多有几个?()
- A、1
- B、2
- C、3
正确答案:A -
第21题:
填空题设A为n阶方阵,E为n阶单位矩阵,且A2=A,则(A-2E)-1=____。正确答案: -(A+E)/2解析:
由题设A2=A有,A2-A-2E=(A-2E)(A+E)=-2E,即(A-2E)[-(A+E)/2]=E,所以有(A-2E)-1=-(A+E)/2。 -
第22题:
单选题三个单位共有180人,甲、乙两个单位人数之和比丙单位多20人,甲单位比乙单位少2人,求甲单位的人数?( )A48人
B49人
C50人
D51人
正确答案: A解析:
设甲单位有x人,则乙单位有(x+2)人,丙单位有(x+x+2-20)人,由题意得,x+x+2+(x+x+2-20)=180,得x=49人。 -
第23题:
单选题五年级学生分成两队参加广播操比赛,排成甲、乙两个实心方阵,其中甲方阵最外层每边的人数为8。如果两队合并,可以另排成一个空心的丙方阵,丙方阵最外层每边的人数比乙方阵最外层每边的人数多4人,且甲方阵的人数正好填满丙方阵的空心。五年级一共有多少人?( )A200
B236
C260
D288
正确答案: B解析:
空心的丙方阵人数=甲方阵人数+乙方阵人数,若丙方阵为实心的,那么实心的丙方阵人数=2×甲方阵人数+乙方阵人数,即实心丙方阵比乙方阵多2×2=128人。丙方阵最外层每边比乙方阵多4人,则丙方阵最外层总人数比乙方阵多4×4=16人,即多了16÷8=2层。这两层的人数即为实心丙方阵比乙方阵多的128人,则丙方阵最外层人数为(128+8)÷2=68人,丙方阵最外层每边人数为(68+4)÷4=18人。那么,共有182-82=260人。
