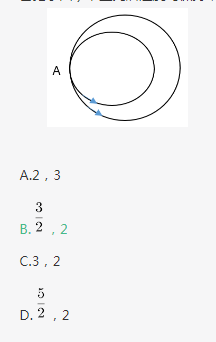
某儿童娱乐场有两条圆形赛车跑道，大圆跑道直径80米，小圆跑道直径60米，两跑道于发车起点A处相切重合。假设甲、乙两辆车同时从A点以相同速度出发（甲跑大圈、乙跑小圈），且此后速度均保持不变。则第一次相距最远时，甲、乙各跑了（ ）圈。

题目
某儿童娱乐场有两条圆形赛车跑道，大圆跑道直径80米，小圆跑道直径60米，两跑道于发车起点A处相切重合。假设甲、乙两辆车同时从A点以相同速度出发（甲跑大圈、乙跑小圈），且此后速度均保持不变。则第一次相距最远时，甲、乙各跑了（ ）圈。

相似考题

1.：甲、乙、丙三人沿着400米环形跑道进行800米跑比赛，当甲跑1圈时，乙比甲多跑17圈。丙比甲少跑17圈。如果他们各自跑步的速度始终不变，那么，当乙到达终点时，甲在丙前面（ ）。A．85米 B．90米 C．100米 D．105米

2.甲、乙、丙三人沿着400米环形跑道进行800米跑比赛，当甲跑l圈时，乙比甲多跑1/7圈。丙比甲少跑1/7圈。如果他们各自跑步的速度始终不变，那么，当乙到达终点时，甲在丙前面（ ）。A．85米B．90米C．100米D．105米

3.周长为400米的圆形跑道上，有相距100米的A．B两点，甲、乙两人分别从A．B两点同时相背而跑，两人相遇后，乙即转身与甲同向而跑，当甲跑到A时，乙恰好跑到B。如果以后甲、乙跑的速度和方向都不变，那么甲追上乙时，甲从出发开始，共跑了（ ）米。A．600B．800C．900D．1 000

4.42 甲、乙、丙三人沿着 400 米 环形跑道进行 800 米 跑比赛，当甲跑 1 圈时，乙比甲多跑 17 圈，丙比甲少跑 17 圈。如果他们各自跑步的速度始终不变，那么，当乙到达终点时，甲在丙前面：A  85 米 B  90 米 C  100 米 105 米

更多“某儿童娱乐场有两条圆形赛车跑道，大圆跑道直径80米，小圆跑道直径60米，两跑道于发车起点A处相切重合。假设甲、乙两辆车同时从A点以相同速度出发（甲跑大圈、乙跑小圈），且此后速度均保持不变。则第一次相距最远时，甲、乙各跑了（ ）圈。 ”相关问题

  • 第1题：

    甲、乙两人从同一起跑线上绕300米环形跑道跑步，甲每秒跑6米，乙每秒跑4米。问第二次追上时，甲跑了几圈?（　　）

    A.6圈　　B.4圈　　C.8圈　　D.2圈


    本题正确答案为A。由于是环形跑道，故当甲第一次追上乙时，甲比乙多跑了一圈；当第二次追上了乙时，说明甲比乙多跑了2圈共600米。甲比乙每秒多跑6-4＝2（米），故多跑600米应当花了甲600/2＝300秒时间。公式为：追及距离（600米）÷速度差（6米-4米）＝追及时间（600/2＝300秒）。甲在300秒后第二次追上了乙，此时甲跑了6米/秒×300秒÷300米/圈＝6圈，故A项正确

  • 第2题：

    甲、乙、丙三人沿着400米环形跑道进行800米跑比赛，当甲跑1圈时，乙比甲多跑1/7圈。丙比甲少跑1/7圈。如果他们各自跑步的速度始终不变，那么，当乙到达终点时，甲在丙前面（ ）


    正确答案：C

  • 第3题：

    甲、乙两人在圆形跑道上，同时从某地出发沿相反方向跑步。甲的速度是乙的3倍，他们第一次与第二次相遇地点之间的较短的跑道长度是100m。那么，圆形跑道的周长是（ ）m。

    A. 200
    B. 300
    C. 400
    D. 500

    答案：C
    解析：
    第一次相遇后，两人仍是沿相反方向跑步，到第二次相遇时，两人跑步距离之和为圆形跑道的周长。此时，乙跑的距离为较短的跑道，为100米，则甲跑的距离为300米，圆形跑道的周长为100 + 300 = 400(米)。故选 C。

  • 第4题：

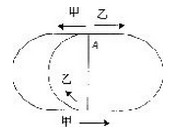
    如图，学校操场的400米跑道中套着300米小跑道．大跑道与小跑道有200米路程相重。甲以每秒6米的速度沿大跑道逆时针方向跑，乙以每秒4米的速度沿小跑道顺时针方向
    跑．NANN 从两跑道的交点A处出发，当他们第二次在跑道上相遇时，甲共跑了多少米?


    A.480
    B.540
    C.660
    D.720

    答案：B
    解析：
    根据题意可知，甲、乙只可能在AB右侧的半跑道上相遇。易知小跑道上AB左侧的路程为100米，右侧的路程为200米，大跑道上AB的左、右两侧的路程均是200米。当甲第一次到达B点时，乙还没有到达8点，所以第一次相遇一定在B点右侧某处。而当乙跑完一圈到达A点需要300．'-4=75秒．甲跑了6×75=450米，在A点左边50米处。所以当甲再次到达B处时，乙还未到B处．那么甲必定能在B点右边某处与乙第二次相遇。从乙再次到达A处开始计算，还需(400—50)÷(6+4)=35秒，甲、乙第二次相遇，此时甲共跑了75+35=110秒，从开始到甲、乙第二次相遇甲共跑了6x110=660米，应选择C。

  • 第5题：

    甲、乙二人绕着圆形操场跑道散步，甲顺时针走，乙逆时针走，两人在跑道A处同时出发，甲每分钟走90米，乙每分钟走60米，当甲、乙两人在跑道B处相遇时，乙加快了速度，甲在原地停留4分钟后保持原来的速度继续往前走，最后甲、乙二人仍在A处相遇。已知该操场的周长为1800米，那么相遇后，乙的速度变为每分钟（ ）米。

    A.70
    B.80
    C.90
    D.100

    答案：C
    解析：
    第一步，本题考查行程问题。
    第二步，甲、乙在B处相遇，根据S=（+）×t代入数据：1800=（90+60）×t，解得t=12（分钟），则甲走了90×12=1080米，乙走了60×12=720米。
    第三步，要回到A处：甲要再走720米，用时720÷90=8分钟，加上原地停留的4分钟，共用时8+4=12分钟，故乙加速后再走1080米也需用时12分钟，加速后的速度为每分钟1080÷12=90米。

  • 第6题：

    某市一体育场有三条同心圆的跑道，里圈跑道长1/5 公里，中圈跑道长1/4 公里，外圈跑道长3/8 公里。甲、乙、丙三人分别在里、中、外圈同一起跑线同时同向跑步。甲每小时跑3.5 公里，乙每小时跑4 公里，丙每小时跑5 公里，问几时后三人同时回到出发点？

    A、8 时
    B、7 时
    C、6 时
    D、5 时

    答案：C
    解析：

  • 第7题：

    周长为400米的圆形跑道上， 有相距100米的A、B两点， 甲乙两人分别从A、B两点同时相背而跑， 两人相遇后， 乙即转身与甲同向而跑步， 当甲跑到A时， 乙恰好跑到B。如果以后甲、乙跑的速度方向都不变，那么甲追上乙时，甲从出发开始，共跑了( )米。

    A．600

    B．800

    C．900

    D．1000


    正确答案：D
    13．D【解析】乙从相遇点C跑回B点时，甲从C过B到A，他比乙多跑了100米，乙从B到C时， 甲从A到C， 说明A到C比B到C多100米， 跑道周长400米， 所以8到C是100米，A到C是200米，甲跑200米，比乙多100米。甲追上乙要多跑300=400—100(米)，所以甲要跑200X 3=600(米)，加上开始跑的一圈，甲共跑600+400=1000(米)。

  • 第8题：

    环形跑道400米，甲、乙两名运动员同时自起点顺时针出发，甲每分钟跑400米，乙每分钟跑375米，问多少分钟后，甲、乙再次相遇？（ ）

    A．14

    B．15

    C．16

    D．17


    正确答案：C
    由题意可得：400÷(400一375)=16(分钟)，即16分钟后，甲比乙多跑一圈。

  • 第9题：

    甲、乙、丙三人沿圆形跑道跑步，同时从跑道某一固定点出发，甲按顺时针方向行走，乙与丙按逆时针方向行走，甲第一次遇到乙2分钟后遇到丙，再过8分钟第二次遇到乙。已知乙的速度是甲的2/3，圆形跑道的周长为600米，则丙的速度为( )。

    A. 14米/分
    B. 15米/分
    C. 16米/分
    D. 17米/分

    答案：A
    解析：
    行程问题。在环形相遇问题中，任意两者相遇一次所走的路程和为一个周长，因此，甲与乙第二次相遇共走的路程（1200米）是第一次相遇共走的路程（600米）的2倍，由于二者速度不变，设第一次的相遇所用时间为t，则第二次相遇时间应为2t，根据题意有2t=t+2+8，解得t=10分钟。再设甲、乙、丙的速度分别为、、，则（+）×10=600，（+V丙）×（10+2）=600，又，解得=36米/分，=14米/分。故本题选择A。

  • 第10题：

    如图，在长方形跑道上，甲、乙两人分别从A、C处同时出发，按顺时针方向沿跑道匀速奔跑。已知甲、乙两人的速度分别为5米/秒、4.5米/秒。则当甲第一次追上乙时，甲沿长方形跑道跑过的圈数是：


    A.4
    B.4.5
    C.5
    D.5.5

    答案：C
    解析：
    起跑时，甲、乙相距20+12=32米，甲每秒比乙多跑5-4.5=0.5米，故甲第一次追上乙需要32/0.5=64秒。跑道一圈为（20+12）x2=64米，故甲第一次追上乙时，甲跑了64x5/64=5圈。

  • 第11题：

    甲乙两人以匀速绕圆形跑道相向跑步，出发点在圆直径的两端。如果他们同时出发，并在甲跑完60米时第一次相遇，乙跑完一圈还差80米时两人第二次相遇，求跑道的长是多少米?()

    A. 200
    B. 400
    C. 800
    D. 1600

    答案：A
    解析：
    由于甲在离A地60米的地方与乙相遇，那么在他们再次相遇的时候甲又走了60米，甲乙再一次相遇在离A地80米处。从A到第一次相遇地点的距离，第一次相遇地点道第二次相遇地点的距离，从A地到第二次相遇地点的距离，这三段距离路程之和刚好是圆形跑道的长度，可见圆形跑道的长度是60+60+80=200米。故答案为A。

  • 第12题：

    单选题
    一条圆形跑道长500米，甲、乙两人从不同起点同时出发，均沿顺时针方向匀速跑步。已知甲跑了600米后第一次追上乙，此后甲加速20%继续前进，又跑了1200米后第二次追上乙。问甲出发后多少米第一次到达乙的出发点？（　　）
    A

    180

    B

    150

    C

    120

    D

    100


    正确答案： A
    解析：
    赋值甲的速度为100米/分，第一次追及，甲跑了600米，用时为6分；第二次追及，甲加速20%，即速度为120米/分，又跑了1200米，用时为10分。行程问题追及公式为：S差＝v差t，从第一次追及开始，到第二次追及时，两人的路程差为1圈，即500＝（120－v乙）×10，解得v乙＝70米/分。分析第一次追及过程可知，甲比乙多走的距离即为甲出发点到乙出发点距离，S差＝v差t＝（100－70）×6＝180米。故正确答案为A。

相关内容