某校下午2点整派车去某厂接劳模作报告，往返须1小时。该劳模在下午1点整就离厂步行向学校走来，途中遇到接他的车，便坐上车去学校，于下午2点40分到达。问汽车的速度 步行速度的多少倍? A. 5倍 B. 6倍 C. 7倍 D. 8倍

题目
某校下午2点整派车去某厂接劳模作报告，往返须1小时。该劳模在下午1点整就离厂步行向学校走来，途中遇到接他的车，便坐上车去学校，于下午2点40分到达。问汽车的速度 步行速度的多少倍?

A. 5倍
B. 6倍
C. 7倍
D. 8倍
相似考题

1.五、应用题（本大题共3小题，共25分）第 18 题 某团体从甲地到乙地，甲、乙两地相距100千米，团体中一部分人乘车先行，余下的人步行，先坐车的人到途中某处下车步行，汽车返回接先步行的那部分人，已知步行速度为8千米／4,时，汽车速度为40千米／小时。问使团体全部成员同时到达乙地需要多少时间?(8分)

2.：某校下午2：00点整派车去某厂接劳模作报告，往返需1小时。该劳模在下午1：00整就离厂步行向学校走来，途中遇到接他的车，便坐上车去学校，于下午2：40到达。问汽车的速度是劳模的步行速度的几倍?（ ）A．5倍B．6倍C．7倍D．8倍

3.甲班与乙班同学同时从学校出发去某公园，甲班步行的速度是每小时4千米，乙班步行的速度是每小时3千米。学校有一辆汽车，它的速度是每小时48千米，这辆汽车恰好能坐一个班的学生。为了使这两班学生在最短的时间内到达，那么，甲班学生与乙班学生需要步行的距离之比是（ ）。A．15：11B．17：22C．19：24D．21：27

4.：某校和某工厂之间有一条公路，该校下午2时派车去该厂接某劳模来校作报告，往返需用l小时。这位劳模在下午1时便离厂步行向学校走来，途中遇到接他的汽车，便立刻上车驶向学校，在下午2时40分到达。问：汽车速度是劳模步行速度的几倍？（ ）A．10B．8C．9D．6

更多“某校下午2点整派车去某厂接劳模作报告，往返须1小时。该劳模在下午1点整就离厂步行向学校走来，途中遇到接他的车，便坐上车去学校，于下午2点40分到达。问汽车的速度 步行速度的多少倍? ”相关问题

  • 第1题：

    某团体从甲地到乙地，甲、乙两地相距100千米，团体中一部人乘车先行，余下的人步行，先坐车的到途中某处下车步行，汽车返回接先步行的那部分人，已知步行速度为8千米/小时，汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间。

    A、5.5小时 B、5小时 C、4.5小时 D、4小时


    正确答案：B

  • 第2题：

    某团体从甲地到乙地，甲、乙两地相距100千米，团体中一部分人乘车先行，余下的人步行，先坐车的人到途中某处下车步行，汽车返回接先步行的那部分人，全部人员同时到达。已知步行速度为8千米/小时，汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间?( )

    A．5.5小时

    B．5小时

    C．4.5小时

    D．4小时


    正确答案：B
    B  [解析]因为两队是同时出发又同时到达的，所以两队步行的距离相等，乘车的距离也相等。设第一队乘车的距离是x，则步行的距离是100-x，那么第二队步行的距离也是100-x，汽车从第一队人下车到回来与第二队相遇的距离是：100-2(100-x)=2x-100，因为汽车从出发到与第二队相遇的时间与第二队步行的时间相同。所以列方程：(z+(2x-100)]÷40=(100-x)÷8，解得x=75，那么一共所用的时间是：75÷40+(100-75)÷8=5(小时)，故选B。

  • 第3题：

    一个人早上从甲地骑自行车，每小时行走10千米，下午1点到达了乙地；没做停留就直接返回甲地，每小时15千米，结果在下午3点40分的时候返回了甲地。这个人第二天早上还是从甲地骑自行车到乙地，相比第一天早上，晚出发了50分钟，但将速度提高了25%，那么他到达乙地的时间应该是（ ）。

    A．下午1点

    B．下午1点O2分

    C．下午1点15分

    D．下午1点28分


    正确答案：B

  • 第4题：

    某高校社团组织远足活动，他们早上8点钟从学校出发，先走了一段平坦的路到达山脚下，然后开始登山。在山顶休息1小时候再原路返回，下午5点钟回到学校。已知他们在平地时的行进速度为每小时8千米，上山速度为每小时6千米，下山速度是上山速度的2倍，那么它们全程共走了( )千米。

    A．48

    B．56

    C．64

    D．72


    正确答案：C
    C [解析]早上8点出发，下午5点回到起点，中间休息了1小时，所以他们行进的时间为8小时。因为下山速度是上山速度的2倍，所以下山速度为6×2=12(千米/时)。设下山用了t小时，上山则用了2t小时，走平路用了8-3t小时，它们全程走的距离为：
    8×(8-3t)+6×2t+12×t=64-24t+12t+12t=64(千米)，故本题答案为C。

  • 第5题：

    甲、乙两班学生到离校24千米的牧场去游玩，有一辆车一次只能乘坐一个班学生，甲、乙 两班步行与乘车交换进行，已知两班步行速度相同，汽车速度是步行速度的7倍，若甲班 先乘车，为使两班同时到达牧场，汽车应在距牧场多远处返回接乙班的学生？（ ）

    A．4.8千米

    B．7.2千米

    C．8.1千米

    D．9千米


    正确答案：A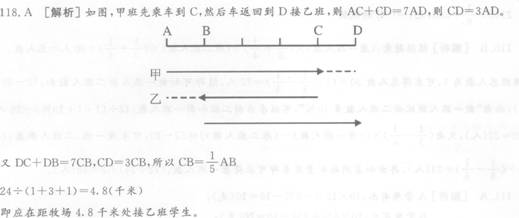

  • 第6题：

    有两个班的小学生要到少年宫参加活动，但只有一辆车接送。第一班的学生坐车从学校出发的同时，第二班学生开始步行；车到途中某处，让第一班学生下车步行，车立刻返回接第二班学生上车并直接开往少年宫。学生步行速度为每小时4公里，载学生时车速每小时40公里，空车每小时50公里。那么，要使两班学生同时到达少年宫，第一班学生步行了全程的几分之几？（学生上下车时间不计）（ ）

    A. 1/7

    B. 1/6

    C. 3/4

    D. 2/5


    正确答案：A
    2. A。【解析】设由学校至少年宫的路程为线段AB，第一班学生坐车至C下车时，第二班学生恰好行至D；空车返回至E恰好与第二班学生相遇；此时第一班学生已由C行至F；第二班学生乘由E行至B时，第一班学生也由F步行至B，两班学生同时到达少年宫。 依题意画出该路程图，不难看出：若以AB 之中点M为中心，则A与B，D与F，E与C形成三组对称点。即AD＝FB，DE＝CF，从而AC＝EB。运用对称性，可知有如下解法： 设AD＝3，由于载人车速为人步行速之10倍，故AC＝30，DC＝27。由于空车速为人步行速之12.5倍，人与空车分别从D、C出发相向而行，至E相遇，故DE＝2，EF＝25。根据对称性知，CF＝2，FB＝3，AB＝（2＋3）×2＋25＝35。第一班学生步行之路程为CB＝2＋3＝5，CB:AB＝5:35＝1/7。

  • 第7题：

    某人下午六点多从甲地步行去乙地，出发时发现表的时针和分针的夹角为1100，
    七点前到达乙地时又看手表，发现时针和分针的夹角仍是110。，
    若此人步行的速度为每小时6千米，则此人以每小时l2
    千米的速度骑车返回需要多少分钟?

    A: 20
    B: 15
    C: 32
    D: 18

    答案：A
    解析：
    此人所用总时间没有超过一个小时，则分针比时针多走的角度小于360。。
    画出示意图，

  • 第8题：

    每天下午4点半小李放学时，妈妈总是从家开车准时到达学校接他回家，某天学校提前一个小时放学，小李自己步行回家，途中遇到开车接他的妈妈，结果比平时提前30分钟到家。若妈妈开车的速度一直保持不变，则小李步行（ ）分钟后与妈妈相遇。

    A.40
    B.45
    C.50
    D.53

    答案：B
    解析：
    第一步，本题考查行程问题，属于相遇追及类
    第二步，根据题意，“比平时提前30分钟到家”说明妈妈少开了30分钟的车，少开的30分钟对应小李所走路程的“来回”部分。因此，妈妈提前15分钟接到小李，平时是4点30分接小李，提前之后是下午4点15分接到小李。“学校提前一个小时放学”，即小李3点30分放学，那么小李步行了4点15分－3点30分＝45分钟。
    因此，选择B选项。

  • 第9题：

    有两个班的学生从南部校区到北部校区参加活动，但只有一辆车接送。第一班的学生坐车从学校出发的同时，第二个班的学生开始步行。车到途中某处，让第一个班的学生下车步行，车立刻返回接第二班学生上车并直接开往北部校区，学生步行速度为每小时4公里，汽车载学生时车速每小时40公里，空车每小时50公里。问：要使两班学生同时到达北部校区，第二班学生要步行全程的（ ）。


    答案：B
    解析：
    第一步，本题考查行程问题。
    第二步，两班同学同时出发，同时到达，又两班学生的步行速度相同，说明两班学生步行的距离和坐车的距离分别相同。设两个班学生步行的距离为x，坐车距离为y，则由题意有x/4=y/40+（y-x）/50，解得x∶y=1∶6，那么x占全程的1/（1+6）=1/7，即第二班的学生步行了全程的七分之一。
    因此，选择B选项。

  • 第10题：

    某人中午十二点从A地出发前往B地，A地路牌上写着“距离B地还有2小时55分钟 步行路程”，下午两点整他在途中一块路牌处停下休息一刻钟，这块路牌写着“距离B地还有I 小时15分钟步行路程”。若他始终保持匀速，到达B地的时间约为：

    A.3:30
    B.3:45
    C.4:20
    D.4:35

    答案：B
    解析：
    AB两地距离为2x60+55=175分钟步行路程,从A地到途中路牌的距离为175-(60+15)=

  • 第11题：

    单选题
    下午(xiàwǔ)我(wǒ)去(qù)学校(xuéxiào)学习(xuéxí)。问(wèn)：他(tā)下午(xiàwǔ)去(qù)哪儿(nǎér)？
    A

    火(huǒ)车(chē)站(zhàn)

    B

    学(xué)校(xiào)

    C

    饭(fàn)馆(guǎn)


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    他下午两点要参加一个会议，现在得去火车站接会议代表。问：他先要去做什么？
    A

    去参观

    B

    上火车

    C

    去接人

    D

    去开会


    正确答案： B
    解析： 暂无解析

  • 第13题：

    小王8点整出门、步行到12千米远的同学家，他步行速度是每小时3千米，但他每走50分钟就要休息10分钟。则他( )时到达。

    A．12:30

    B．12:35

    C、12:20

    D．12:40


    正确答案：D
    19．【答案】D。解析：小王实际的步行时间为12÷3=4小时=240分钟，240÷50=4......40，因此他一共休息了4次，共40分钟，则小王12:40到达目的地。

  • 第14题：

    某校下午2点整派车去某厂接劳模作报告，往返须1小时，该劳模在下午1点整就离厂步行向学校走来，途中遇到接他的车，便坐上车去学校，于下午2点40分到达，问汽车的速度是劳模的步行速度的多少倍？( )

    A.5倍

    B.6倍

    C.7倍

    D.8倍


    正确答案：D

  • 第15题：

    小文9点整出门，步行去10千米远的爷爷家，他步行速度是3千米／时，可是他每走40分钟就要休息10分钟，则小文到达爷爷家的时间是（ ）点。

    A．10

    B．11

    C．12

    D．13


    正确答案：D
    小文50分钟里走40分钟，走了3×(40／50)＝2(千米)，10千米中共有5个2千米，而最后一个2千米，小文只需要走完40分钟即可，不需要再休息10分钟，因此小文走到爷爷家总共用的时间是50×4＋40＝240(分钟)，即4个小时，9＋4＝13。本题正确答案为D。

  • 第16题：

    甲、乙两班同学同时去离学校12.1千米的陵园，甲班先乘车后步行，乙班先步行，当送甲班同学的车回来时乙即乘车前去。两班步行速度都是每小时5千米，车速度都是每小时40千米，已知两班同时到达陵园，那么甲在离陵园多远地方下车？（ ）

    A．2千米

    B．2.2千米

    C．2.5千米

    D．3千米


    正确答案：B
    甲、乙两班同时到达，表明两班乘车路程与步行路程分别相同。设甲班在离陵园x千米处下车改为步行，则有：

    即甲班在离陵园2.2千米处下车改为步行。

  • 第17题：

    某校和某工厂之间有一条公路，该校下午2时派车去该厂接某劳模来校作报告，往返需用1小时。这位劳模在下午1时便离厂步行向学校走来，途中遇到接他的汽车，便立刻上车驶向学校，在下午2时40分到达。问：汽车速度是劳模步行速度的几倍？( )

    A．10

    B．8

    C．9

    D．6


    正确答案：B
    B【解析】汽车走单程需要60÷2=30分钟，实际走了40÷2=20分钟的路程，说明相遇时间是2时20分。相遇时，劳模走了60+20=80分钟，这段距离汽车要走30-20=10分钟，所以  车速/劳模车速=80/10=8。故答案为B。

  • 第18题：

    某校下午2点整派车去某厂接劳模作报告，往返须1小时。该劳模在下午1点整就离厂步行向学校走来，途中遇到接他的车，便坐上车去学校，于下午2点40分到达。问汽车的速度是步行速度的多少倍?

    A．5倍

    B．6倍

    C．7倍

    D．8倍


    正确答案：D
    [答案] D。解析：分析题意可知：整个过程中车行驶了40分钟，人共走了60+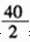=80分钟。设车的速度为x，人的速度为y，则(40÷2)x+80y=(60÷2)x,x=8y，选D。

  • 第19题：

    甲、乙两车分别从A、B两地同时相向而行，已知甲车速度与乙车速度之比为4：3，C地在A、B之间，甲、乙两车到达C地的时间分别是上午8点和下午3点，问甲、乙两车相遇是什么时间?（　）

    A.上午9点
    B.上午10点
    C.上午11点
    D.下午1点

    答案：C
    解析：
    设乙车速度为3，那么甲车速度就是4。从甲到达C地开始算起。乙到达C地走过的路程为(15-8)×3=21。那么在这段路程两人相遇需要花费21÷(3+4)=3小时，他们相遇是在8点之后3小时即11点。

  • 第20题：

    某校下午2点整派车去某厂接劳模作报告，往返须l小时。该劳模在下午1点整就离厂步行向学校走来，途中遇到接他的车，便坐上车去学校，于下午2点40分到达。问汽车的速度是劳模的步行速度的多少倍?（ ）
    A．5倍 B．6倍 C．7倍 D．8倍


    答案：D
    解析：

  • 第21题：

    司机每天按规定时间开车从工厂到厂长家接厂长。一天厂长提前了1小时出门。沿路先步行，而司机晚出发了4分钟，途中接到厂长，结果厂长早到厂8分钟，那么开车速度与厂长步行速度的比是多少?

    A.9：1
    B.10：1
    C.11：1
    D.12：1

    答案：C
    解析：
    司机晚出发4分钟。又早到8分钟，那么相当于少用4+8=12分钟时间接厂长到厂，又知道司机来回的时间是相等的，故司机去的时候少用12÷2=6分钟。而司机这6分钟走的路程是厂长步行的路程，厂长走这段路的时间应该是早出发的1小时加上司机遇到厂长时少用的6分钟，共66分钟。根据分析，相同的路程情况下，司机的速度与厂长步行的速度比是66：6=11：1，应选择C。

  • 第22题：

    有两个班的小学生要到少年宫参加活动，但只有一辆车接送，第一班的学生坐车从学校出发的同时，第二班学生开始步行；车到途中某处，让第一班的学生下车步行，车立刻返回接第二班学生上车，并直接开往少年宫，学生步行速度为每小时4千米，载学生时车速每小时40千米，空车每小时50千米。问：要使两班学生同时到达少年宫，第一班学生步行了全程的几分之几？（学生上下车时间不计）（）


    答案：D
    解析：
    根据题意，两个班的同学都是一段路步行一段路乘车，而乘车的速度比步行快，中间又没有停留，因此要同时到达少年宫，两个班的同学步行的路程一定要一样长。

    如图所示，A是学校，B是少年宫，C是第一班学生下车的地点，D是第二班学生上车的地点。由题意得，AD=BC，学生步行的时间与车从A开到C再回到D的时间相等。设AD=BC=x，CD=y，则有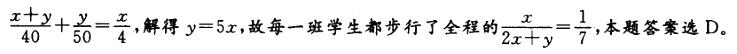

  • 第23题：

    单选题
    约定还款扣款时间为（）。
    A

    到期还款日下午五点之后

    B

    到期还款日下午五点之前

    C

    到期还款日下午五点整

    D

    到期还款日当天任意时间


    正确答案： D
    解析： 暂无解析

  • 第24题：

    单选题
    下午(xiàwǔ)我(wǒ)没(méi)去(qù)学校(xuéxiào)，我(wǒ)在家(zàijiā)学习(xuéxí)。问(wèn)：下午(xiàwǔ)她(tā)在(zài)哪儿(nǎér)？
    A

    家里(jieli)

    B

    学校(xuéxiào)

    C

    医院(yīyuàn)


    正确答案： A
    解析： 暂无解析

相关内容