一个木制正方体在表面涂上颜色，将它的每条棱三等分，然后从等分点将正方体展开，得到27个小正方体，将这些小正方体充分混合后，装入一个口袋，从这个口袋中随机取出两个小正方体，其中一个正方体只有一个面涂有颜色，另一个只有2个面涂有颜色的概率约为（ ）A. 0.05 B. 0.17 C. 0.34 D. 0.67
题目
一个木制正方体在表面涂上颜色，将它的每条棱三等分，然后从等分点将正方体展开，得到27个小正方体，将这些小正方体充分混合后，装入一个口袋，从这个口袋中随机取出两个小正方体，其中一个正方体只有一个面涂有颜色，另一个只有2个面涂有颜色的概率约为（ ）
A. 0.05
B. 0.17
C. 0.34
D. 0.67
B. 0.17
C. 0.34
D. 0.67
相似考题
更多“一个木制正方体在表面涂上颜色，将它的每条棱三等分，然后从等分点将正方体展开，得到27个小正方体，将这些小正方体充分混合后，装入一个口袋，从这个口袋中随机取出两个小正方体，其中一个正方体只有一个面涂有颜色，另一个只有2个面涂有颜色的概率约为（ ）”相关问题
-
第1题：
将27个边长为1的小正方体垒成一个大正方体，然后把大正方体全部涂成红色，请问：三面都被涂成红色的小正方体有多少个？（）。
A.4
B.6
C.8
D.12
正确答案：C
只有正方体8个顶点处的小正方体三面都被涂成红色。故选C。 -
第2题：
一个正方体木块的体积为1000厘米³，现要把它锯成八块，同样大小的正方体小木块，小木块的棱长是多少？
锯成8块之后，每小块的正方体体积为1000/8=125厘米³
设小木块的棱长是x，则
x³=125，x=5厘米
-
第3题：
将右边的箔片沿虚线折起来，便可做一个正方体。问这个正方体的3号面对面是几号面？( )
A.1
B.2
C.5
D.6
正确答案：D
-
第4题：
一块各面均涂有油漆的正方体被锯成1000个同样大小的小正方体，将这些小正方体均匀地搅混在一起，随机地取出一个小正方体，其两面涂有油漆的概率是：A.0.12
B.0.096
C.0.072
D.0.064答案：B解析：1000＝10×10×10，即每个边上有10块，两面涂有油漆的只能在边上，共有（10－2）×12＝96块，概率为96÷1000＝0.096。 -
第5题：
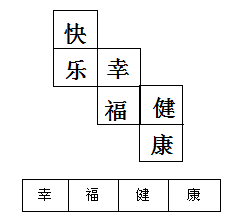
下面是一个水平放置的正方体的表面展开图，若图中“快”是正方体的上面，则这个正方体的下面是
A. A
B. B
C. C
D. D答案：B解析：从题干的平面展开图可以判断出“快”与“福”、“幸”与“康”、“乐”与“健”是相对面关系，所以题中所求“快”是正方体的上面，它的下面为其相对面“福”。故答案选B。 -
第6题：
边长为6的正方体，由若干个边长为1的正方体组成，现将大正方体表面涂上色，请问仅有一面着色的小正方体与仅有两面着色的小正方体个数之差为多少？A.36
B.48
C.54
D.64答案：B解析：本题属于几何问题。
正方体六面八个顶点十二条棱。仅有两面着色的是每条棱上的4个小正方体，总计4×12=48个；仅有一面着色的是每个面中间的4×4=16个正方体，六个面总共有=4×4×6=96个；故个数之差=96-48=48，B选项正确。
因此，选择B选项。 -
第7题：
将1000个边长为1cm的小正方体组合成一个实心的大正方体后，将该正方体的5个面涂满色后再全部分开，那么至少有一面涂色的小正方体有多少个？A.424
B.488
C.512
D.576答案：A解析：解法一：
第一步，本题考查几何问题，属于立体几何类。
第二步，由题意可知大正方体的边长为10cm（10^3=1000），此正方体外表面5个面涂满色，则被涂色小正方体侧面有10×（4×10-4）=360（个），底面有8×8=64（个），共有360+64=424（个）。
因此，选择A选项。
解法二：
第一步，本题考查几何问题，属于立体几何类。
第二步，由题意可知大正方体的边长为10cm（10^3=1000），未被涂色小正方体为（8×8×9）-（8×8）=8×8×9=576（个），被涂色的小正方体有1000－576=424（个）。 -
第8题：
将2个棱长为30厘米的正方体木块的六面分别全涂成黑色后，都锯成棱长为10厘米的小正方体，问从这些小正方体中随机抽取出多少个，才能保证一定能够在取出的小立方体中挑出8个，拼成外表面全为黑色的，棱长为20厘米的正方体？A. 27
B. 36
C. 40
D. 46答案：D解析：【答案】D。解析：满足要求的小正方体要求三个面是黑色的，大正方体能分割成27×2=54个小正方体，只有角上的正方体满足要求，共16个，不满足的38个，若要保证一定能组成的话共需要抽出38+8=46个。答案选D。 -
第9题：
把若干个体积相等的正方体拼成一个大正方体,在表面涂上红色,已知一面涂色的小正方体有96个,则两面涂色的小正方体有（ ）个A.48
B.60
C.64
D.24
E.32答案：A解析：一面涂色的小正方体位于大正方体的面上（除去機上的）,每个面有4×4=16（个）,令小正方体的边长为1,则大正方体的边长为6;两面涂色的小正方体位于大正方体的機上（除去8个角）,每条棱上有4个,故总个数为4×12=48 -
第10题：
有64个棱长为1厘米的同样大小的小正方体，其中34个为白色的，30个为黑色的。现将它们拼成一个4X4X4的大正方体，在大正方体的表面上白色部分最多可以是多少平方厘米？（ ）
A. 52 B. 64 C. 72 D. 74答案：D解析：没有露在表面的小正方体有(4一2)3=8(个)是用黑色的。在面上但不在棱上的小正方体有(4-2)2X6 = 24(个)，其中30-8 = 22(个)用黑色的。这样，在表面积为4X4X6 = 96(平方厘米)的小正方形中，22个是黑色，共22平方厘米，有96-22 = 74(平方厘米)是白色，在大正方体的表面上白色部分最多可以是74平方厘米。因此，本题正确答案为D。 -
第11题：
边长为4的正方体木块，各面均涂成红色，将其锯成64个边长为1的小正方体，并将它们搅匀混在一起，随机取出一个小正方体，恰有两面为红色的概率是（ ）。
答案：A解析：本题主要考查概率的计算及空间想象能力。根据题意，是将大正方体分成四层，每层16个小正方体，两个面都为红色的处于上（除过顶点处），每条棱有2个，12条棱共有24个符合条件的小正方体，因此取到面为红色的小正方体的概率为
-
第12题：
把一个64cm×40cm×24cm的长方体切成若干个完全相同的小正方体，并使这些小正方体的表面积总和最小，则小正方体的表面积总和为（ ）。
A．73280cm2
B．54680cm2
C．69450cm2
D．46080cm2
正确答案：D
要使这些小正方体的表面积总和最小，那么小正方体的边长要尽可能大。64、40、24的最大公约数为B，因此小正方体的边长为8cm，共有64×40×24÷83=120块。表面积总和为6×82×120=46080cm2。 -
第13题：
有64个边长为l厘米的同样大小的小正方体， 其中34个为白色的，30个为黑色的。现将它们拼成一个4×4×4的大正方体， 在大正方体的表面上白色部分最多可以是多少平方厘米?( )
A．52
B．64
C．72
D．74
正确答案：D
-
第14题：
把一个64Cmx40Cmx24Cm的长方体切成若干个完全相同的小正方体，并使这些小正方体的表面积总和最小，则小正方体的表面积总和为（ ）。
A．73280cm2
B．54680cm2
C．69450cm2
D．46080cm2
正确答案：D
要使这些小正方体的表面积总和最小，那么小正方体的边长要尽可能大。64、40、24的最大公约数为8，因此小正方体的边长为8cm，共有64×40×24÷83＝120块。表面积总和为6×82×120＝46080cm2。 -
第15题：
在棱长为1的正方体上切下两个角，所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体，六面体体积为原正方体体积的1/24，则六面体表面积为原正方体表面积的：A.1/4
B.1/6
C.1/8
D.1/10答案：C解析：由题意知切下的角是底面为正三角形、侧面为三个等腰直角三角形的三棱锥，设切下角的直角边为ｘ，则六面体体积＝2×三棱锥体积＝2×(1/3)×(ｘ2/2)×ｘ＝1/24，解得ｘ＝1/2。所以六面体每个面是直角边为1/2的等腰直角三角形，六面体的每个面相当于边长为1的正方形面积的1，所以六面体的表面积为原正方体的1/8。故本题选C。 -
第16题：
1000个体积为1立方厘米的小正方体合在一起成为一个边长为10厘米的大正方体，大正方体表面涂油漆后，再分开为原来的小正方体，这些小正方体至少有一面被油漆涂过的数目是多少个：
A 490
B 488
C 484
D 480答案：B解析：
-
第17题：
有l25个棱长均为1的正方体，其中100个表面为白色，25个表面为蓝色。将这些正方体组成一个大正方体，表面为白色的面积至少为( )。’A.100
B.97
C.94
D.92答案：D解析：题目可转化为表面为蓝色的面积至多为多少，则应把蓝色小正方体尽量放在角和棱上，这样每个小正方体可贡献3个或2个蓝色表面。因此在8个角上用去8个蓝色正方体后，在棱上再放25—8=17个，此时蓝色表面积最大为3×8+17x2=58，表面为白色的面积至少为25×6—58=92．选D。 -
第18题：
有一批边长为1厘米的小正方体，其中一面涂红色的有400个，相邻两面涂红色的有30个，相邻三面涂红色的有1个，其余小正方体各面都没有涂颜色。用这一批小正方体组成一个大正方体，要求这个大正方体有三个面是红色，且这三个面两两相邻，其余的三个面没有颜色。假如没有涂颜色的小正方体数量足够多，那么这个正方体的边长最大是（ ）厘米。A.10
B.11
C.12
D.13答案：B解析：第一步，本题考查几何问题，属于几何构造。
第二步，让三面都涂色的小正方体作为一个顶角，然后与其相相连的三个棱均放置相邻两个面涂色的小正方体，每条棱上各10个，此时需要需要单面涂色的小正方体10×10×3＝300（个），可以满足，故边长最长为10＋1＝11（厘米）。 -
第19题：
一千个体积为1立方厘米的小正方体合在一起成为一个边长为10厘米的大正方体，大正方体表面涂油漆后再分开为原来的小正方体，这些小正方体至少有一面被油漆涂过的数目是( )个。A.490
B.488
C.484
D.480答案：B解析：分析：没有涂色的小正方体都在大正方体的内部，由此先借助正方体的体积公式求出没有涂色的小正方体的个数即可解答．
解答：解：没有涂色的小正方体：
（10-2）×（10-2）×（10-2）=8×8×8=512（个），
所以至少一面涂色的小正方体：1000-512=488（个） -
第20题：
将一个8厘米×8厘米×1厘米的白色长方体木块的外表面涂上黑色颜料，然后将其切成64个棱长1厘米的小正方体，再用这些小正方体堆成棱长4厘米的大正方体，且使黑色的面向外露的面积要尽量大，问大正方体的表面上有多少平方厘米是黑色的？A. 88
B. 84
C. 96
D. 92答案：A解析：白色长方体可以看做64个小正方体平铺，由4个角，24个棱和36个中间小正方体构成，角上的4个小正方体有4个面被刷成了黑色，棱上的24个小正方体连续的3个面被刷成了黑色，中间的36个小正方体相对的2个面被刷成了黑色；拼成的大正方体有8个角，24个棱和24个单面，拼接时有4个角需用之前棱上的小正方体替换，每替换一次缺一个黑色面，角上共缺了4个；由于4个棱上的正方体替换到了角上，此时棱上又少了4个小正方体，需用对面为黑色的小正方体替换，每替换一次缺一个黑色面，棱上共缺了4个。大正方体的表面积为4×4×6=96平方厘米，大正方体的表面上共有96-4-4=88平方厘米是黑色的。因此，本题选A。 -
第21题：
边长为4的正方体木块，各面均涂成红色，将其锯成64个边长为1的小正方体，并将它们搅匀混在一起，随机抽取一个小正方体，恰有两面为红色的概率是（ ）
答案：A解析：锯成64个边长为1的小正方体后，涂色的面有以下几种情况：涂3面的小正方体分别在大正方体的8个顶点处，共有8个；涂2面的小正方体分别是大正方体的每条棱的中间的2个，而大正方体共有12条棱，那么，涂2面的小正方体有2×12=24个；涂1面的小正方体分别是每个面的中间的4个，而大正方体共有6个面，那么，涂1面的小正方体有4×6=24个；6个面都没有涂色的小正方体有64-8-24-24=8个，则随机抽取一个小正方体，恰有两面为红色的概率是
