随机抽查某地250名健康成年女子的身高，算得均数为160cm，标准差为6cm，则变异系数为A、160/6B、6/160C、(160/6)cmD、(6/160)cmE、(6/250)cm该地95%健康成年女子的身高范围(cm)为A、(160±1.64×6)B、(160±1.96×6)C、(160±2.58×6)D、(160±1.64×6/250)E、(160±1.96×6/250)
题目
随机抽查某地250名健康成年女子的身高，算得均数为160cm，标准差为6cm，则变异系数为A、160/6
B、6/160
C、(160/6)cm
D、(6/160)cm
E、(6/250)cm
该地95%健康成年女子的身高范围(cm)为A、(160±1.64×6)
B、(160±1.96×6)
C、(160±2.58×6)
D、(160±1.64×6/250)
E、(160±1.96×6/250)
相似考题
更多“随机抽查某地250名健康成年女子的身高，算得均数为160cm，标准差为6cm，则变异系数为A、160／6B、6／160 ”相关问题
-
第1题：
据大量调查知，健康成年男性身高的均数为170.0cm，某医生在某山区随机调查了30名健康成年男性，其身高均数为168.9cm，标准差为9.7cm。欲估计该医生此次调查的山区健康成年男性身高的抽样误差，计算公式为
A.S
B.σ
C.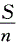
D.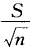
E.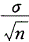
答案：D解析：
1题：资料分为定量资料和分类资料两类，定量资料又分为连续型和离散型定量资料，健康成年男性的身高为连续型定量资料，故选项E正确。2题：标准误是衡量抽样误差大小的指标，均数标准误的估计公式为：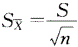
，故选项D正确。3题：选项A是服从正态分布的资料的95%医学参考值范围的计算公式，选项B是当n足够大时总体均数的95%置信区间的计算公式。本题总体标准差σ未知，按t分布的原理估计总体均数的100（1-a）%置信区间的公式为：
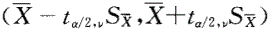。本题欲估计该山区健康成年男性身高均数的95%置信区间，故取a=0.05，自由度ν=n-1=30-1=29，故选项C、D错误，选项E正确。4题：本题资料宜用样本均数与总体均数比较的t检验，检验统计量的计算公式为：
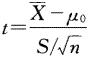，故选项D正确。 -
第2题：
据大量调查知，健康成年男性身高的均、数为170.0cm，某医生在某山区随机调查了30名健康成年男性，其身高均数为168.9cm，标准差为9.7cm。欲比较该山区健康成年男性与一般健康成年男性的身高是否有差异，检验统计量的计算公式为( )
A.
B.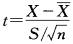
C.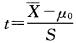
D.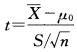
E.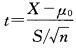
答案：D解析：
-
第3题：
据大量调查知，健康成年男性身高的均、数为170.0cm，某医生在某山区随机调查了30名健康成年男性，其身高均数为168.9cm，标准差为9.7cm。欲估计该医生此次调查的山区健康成年男性身高的抽样误差，计算公式为( )
A.S
B.σ
C.S/n
D.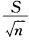
E.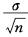
答案：D解析： -
第4题：
据大量调查知，健康成年男性身高的均数为170.0cm，某医生在某山区随机调查了30名健康成年男性，其身高均数为168.9cm，标准差为9.7cm。欲估计该山区健康成年男性身高均数的95%置信区间，计算公式为
A.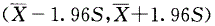
B.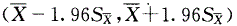
C.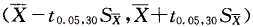
D.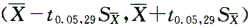
E.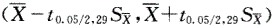
答案：E解析：
1题：资料分为定量资料和分类资料两类，定量资料又分为连续型和离散型定量资料，健康成年男性的身高为连续型定量资料，故选项E正确。2题：标准误是衡量抽样误差大小的指标，均数标准误的估计公式为：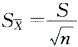
，故选项D正确。3题：选项A是服从正态分布的资料的95%医学参考值范围的计算公式，选项B是当n足够大时总体均数的95%置信区间的计算公式。本题总体标准差σ未知，按t分布的原理估计总体均数的100（1-a）%置信区间的公式为：
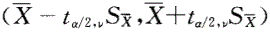。本题欲估计该山区健康成年男性身高均数的95%置信区间，故取a=0.05，自由度ν=n-1=30-1=29，故选项C、D错误，选项E正确。4题：本题资料宜用样本均数与总体均数比较的t检验，检验统计量的计算公式为：
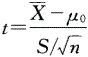，故选项D正确。 -
第5题：
据大量调查知，健康成年男性身高的均、数为170.0cm，某医生在某山区随机调查了30名健康成年男性，其身高均数为168.9cm，标准差为9.7cm。欲估计该山区健康成年男性身高均数的95%置信区间，计算公式为( )
A.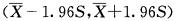
B.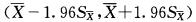
C.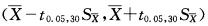
D.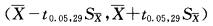
E.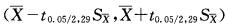
答案：E解析：