某班有36名同学参加数学、物理、化学课外探究小组，每名同学至多参加两个小组，已知参加数学、物理、化学小组的人数分别为26，15，13，同时参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，则同时参加数学和化学小组的有 人。

题目

某班有36名同学参加数学、物理、化学课外探究小组，每名同学至多参加两个小组，已知参加数学、物理、化学小组的人数分别为26，15，13，同时参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，则同时参加数学和化学小组的有 人。

相似考题

1. 我们班2/5的同学参加了舞蹈小组，4/10的同学参加了书法小组，哪个小组的人数多？

2.五（1）班有25人，许多同学参加了课外小组。参加音乐组的有12人，参加美术组的有10人，两个组都没参加的有6人。既参加音乐组又参加美术组的有多少人？

3.：某班有50名学生，参加语文竞赛的有28人，数学23人，英语20人，每人至多参加两科，那么参加两科的最多有（ ）人。A．28B．25C．23D．21

4.甲、乙两班的同学人数相等，各有一些同学参加课外天文小组。甲班参加天文小组的人数恰好是乙班没有参加的人数的1/3，乙班参加天文小组的人数是甲班没有参加的人数的四分之一。问甲班没有参加的人数是乙班没有参加的人数的几分之几?

参考答案和解析
正确答案：
答案：8
更多“某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理 ”相关问题

  • 第1题：

    数学课外活动小组有8名男同学和5名女同学。从这些同学中选出3人参加市数学竞赛，其中至少有1名女同学，一共有多少种选法?（ ）

    A．140

    B．150

    C．230

    D．286


    正确答案：C

  • 第2题：

    某班有50名学生，参加语文竞赛的有28人，参加数学竞赛的有23人，参加英语竞赛的有20人，每人至多参加两科，那么参加两科的最多有多少人?（ ）

    A．28

    B．35

    C．39

    D．42


    正确答案：B

  • 第3题：

    某班有35个学生．每个学生至少参加英语小组、语文小组、数学小组中的一个课外活动小组。现已知参加英语小组的有17人，参加语文小组的有30人，参加数学小组的有13人。如果有5个学生三个小组全参加了，问有多少个学生只参加了一个小组（ ）

    A．15人

    B．16人

    C．17人

    D．18人


    正确答案：A
    设选两门课的人数为A，有(13+17+30)-A-2×5=35，得A=15。所以只报一门的人数为35-15-5=15。

  • 第4题：

    某班有40名学生，其中有15人参加数学小组，18人参加航模小组，有10人两个小组 都参加．那么有多少人两个小组都不参加?（ ） A．16 B．17 C．18 D．19


    正确答案：B
    依据题意，只参加数学小组的同学有15—10=5人，只参加航模小组的同学有18－10＝8人，两个小组都参加的同学有10人，所以有40一23＝17人两个小组都不参加。故选B。

  • 第5题：

    某班有50名学生，参加语文竞赛的有28人，参加数学竞赛的有23人，参加英语竞赛的有20人，每人至多参加两科，那么参加两科的最多有多少人？（ ）

    A. 28
    B. 35
    C. 39
    D. 42

    答案：B
    解析：
    画出图示，因为“每人最多参加两科”，所以没有人参加三科竞赛。由图可知：

  • 第6题：

    某班有60人，参加物理竞赛的有30人，参加数学竞赛的有32人，两科都没有参加的有20人。同时参加物理、数学两科竞赛的有多少人：

    A28人
    B26人
    C24人
    D22人


    答案：D
    解析：

  • 第7题：

    某班有36名同学参加数学、物理、化学课外研究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有（ ）

    A.6人
    B.7人
    C.8人
    D.9人
    E.10人

    答案：C
    解析：
    由条件知,每名同学至多参加两个小组,故不可能出现一名同学同时参加数学、物理、化学课外研究小组,设同时参加数学和化学小组的有x人,根据容斥原理有26+15+13-（6+4+x）=36,解得x=8.故同时参加数学和化学小组的有8人,应选C.

  • 第8题：

    某班有60人，参加物理竞赛的有30人，参加数学竞赛的有32人，两科都没有参加的有20人。同时参加物理、数学两科竞赛的有多少人？

    • A、28人 
    • B、26人 
    • C、24人 
    • D、22人

    正确答案:D

  • 第9题：

    单选题
    某班有50位同学参加期末考试，结果英文不及格的有15人，数学不及格的有19人，英文和数学都及格的有21人。那么英文和数学都不及格的有（　　）人。
    A

    4

    B

    5

    C

    13

    D

    17


    正确答案： B
    解析：
    设英文和数学都不及格的有x人，由容斥原理可得15＋19－x＝50－21，得x＝5。

  • 第10题：

    丹丹、小颖、淑珍去参加奥林匹克竞赛。奥林匹克竞赛有数学、物理和化学三种，每人只参加一种。建国、小杰、大牛做了以下猜测：

    建国：丹丹参加了数学竞赛，小颖参加了物理竞赛。

    小杰：淑珍没参加物理竞赛，小颖参加了数学竞赛。

    大牛：丹丹没参加数学竞赛，小颖参加了化学竞赛。

    如果他们的猜测都对了一半，则以下哪项为真?（ ）

    A．丹丹、小颖、淑珍分别参加了数学、物理和化学竞赛

    B．丹丹、小颖、淑珍分别参加了物理、数学和化学竞赛

    C．丹丹、小颖、淑珍分别参加了数学、化学和物理竞赛

    D．丹丹、小颖、淑珍分别参加了化学、物理和数学竞赛


    正确答案：D
    【解析】根据三个人的猜测各对了一半，可以得到三个人所做的猜测都构成了一个不相容的选择命题，其中，都是有并且只有一个部分是对的。设丹丹参加了数学竞赛，则小颖没有参加物理竞赛，小颖也没有参加数学竞赛，小颖只能参加化学竞赛。但是，这样会导致淑珍没参加物理竞赛，但淑珍也不能参加数学竞赛和化学竞赛，于是，出现了矛盾。所以，丹丹没有参加数学竞赛。于是，小颖参加了物理竞赛，没有参加数学竞赛和化学竞赛。根据丹丹和小颖都没有参加数学竞赛，可以推出淑珍参加数学竞赛。所以，丹丹参加化学竞赛。

  • 第11题：

    某班有50名学生，参加英语竞赛的有28人，参加数学竞赛的有20人，参加物理竞赛的有23人，每人最多参加两科，那么只参加两科的最多有多少人?

    A．23

    B．35

    C．28

    D．21


    正确答案：B
    94．【答案】B。解析：参加竞赛的有28+20+23=71人次，要使参赛的人尽可能地参加两科，71÷2=35??l，所以至多有35人参加两科。

  • 第12题：

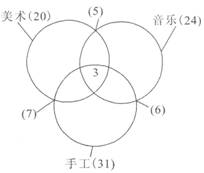
    某年级的课外小组分为美术、音乐、手工三个小组，参加美术小组有20人，参加音乐小组有24人，参加手工小组有31人，同时参加美术和音乐两个小组有5人，同时参加音乐和手工两个小组有6人，同时参加美术和手工两个小组的有7人，三个小组都参加的有3人，这个年级参加课外小组的同学共有多少人?（ ） A．75人 B．57人 C．63人 D． 60人


    正确答案：D
    如图所示，由容斥原理可知，这个年级参加课外小组的有20+24+31－(5+6+7)+3＝60人。故选D。

  • 第13题：

    数学老师将上微积分课的一部分学生组成一个学习小组，学习小组的成员获得的平均分要比没有参加学习小组的学生高许多。数学系把小组成员的好成绩归功于参加了学习小组。上述推理的假设是什么?

    A．对老师来讲，微积分是一门很难向一大组学生讲解的课程。

    B．参加学习小组的同学与没有参加学习小组的同学相比，既没有专门准备，也没有受到太多激励。

    C．小组成员花在微积分上的时间并没有影响他们其他课程的成绩。

    D．参加学习小组的同学中很少有人打算学习比微积分更高级的其他数学课。


    正确答案：B
    解析：题干论述：因为参加学习小组，所以成绩好。此类假设往往是：没有其他的原因来解释上面这个事实。既然归功于学习小组，应该跟老师的讲课无关，A项为无关选项。B项表明没有其他的原因，正确。C、D项是无关项。

  • 第14题：

    某班参加学科竞赛人数40人，其中参加数学竞赛的有22人，参加物理竞赛的有27人，参加化学竞赛的有25人，只参加两科竞赛的有24人，参加三科竞赛的有多少人？

    A.2
    B.3
    C.5
    D.7

    答案：C
    解析：
    第一步，本题考查容斥问题，属于三集合容斥类，用公式法解题。
    第二步，设参加三科竞赛的有x人，根据三集合非标准型容斥原理公式可列方程：40－0＝22＋27＋25－24－2x，解得x＝5。

  • 第15题：

    某单位乒乓球，羽毛球，篮球三个兴趣小组共有72人参加。已知同时参加3个小组的人数为0，只参加羽毛球小组的人数是只参加乒乓球小组人数的4倍，只参加篮球小组的有11人，同时参加两个小组的人数与只参加1个小组的人数相同，参加乒乓球小组但未参加篮球小组的人中有一半参加羽毛球小组，问参加包括篮球在内的两个小组的有：

    A.32人
    B.31人
    C.25人
    D.24人

    答案：B
    解析：
    第一步，本题考查容斥原理。
    第二步，设只参加乒乓球小组人数为x，则只参加羽毛球小组的人数为4x，只参加一个小组和同时参加两个小组的人数都为x+4x+11=5x+11，有2×（5x+11）=72，解得x=5。由题意篮球之外的乒乓球小组人数是只参加乒乓球小组人数的2倍，则参加乒乓球小组但未参加篮球小组的人数是10，那么参加包括篮球在内的两个小组的有72－10－20－11=31（人）。
    因此，选择B选项。

  • 第16题：

    有些甲班同学没有参加书法小组，小吴参加书法小组，所以小吴不是甲班同学。混合关系三段论的形式是否有效？为什么？


    正确答案: 无效。因为它违反前提中不周延的项在结论中也不得周延的规则。

  • 第17题：

    问答题
    有些甲班同学没有参加书法小组，小吴参加书法小组，所以小吴不是甲班同学。混合关系三段论的形式是否有效？为什么？

    正确答案： 无效。因为它违反前提中不周延的项在结论中也不得周延的规则。
    解析： 暂无解析

相关内容