某家庭购买了一套90m2的商品住宅,售价为4000元/m2。该家庭首付了房价总额的30%,其余购房款申请住房公积金和商业组合抵押贷款。住房公积金贷款和商业贷款的利率分别是4.5%和6.8%,贷款期限为15年,按月等额偿还。其中住房公积金贷款的最高限额为10万元。如果该家庭以月收入的35%用来支付抵押贷款月还款额,那么此种贷款方案要求该家庭的最低月收入为多少?假设该家庭在按月还款3年后,于第4年初一次性提前偿还商业贷款本金5万元,那么从第4年起该家庭的抵押贷款的月还款额为多少?
题目
某家庭购买了一套90m2的商品住宅,售价为4000元/m2。该家庭首付了房价总额的30%,其余购房款申请住房公积金和商业组合抵押贷款。住房公积金贷款和商业贷款的利率分别是4.5%和6.8%,贷款期限为15年,按月等额偿还。其中住房公积金贷款的最高限额为10万元。如果该家庭以月收入的35%用来支付抵押贷款月还款额,那么此种贷款方案要求该家庭的最低月收入为多少?假设该家庭在按月还款3年后,于第4年初一次性提前偿还商业贷款本金5万元,那么从第4年起该家庭的抵押贷款的月还款额为多少?
相似考题
更多“某家庭购买了一套90m2的商品住宅,售价为4000元/m2。该家庭首付了房价总额的30%,其余购房款申请住房公积金和商业组合抵押贷款。住房公积金贷款和商业贷款的利率分别是4.5%和6.8%,贷款期限为15年,按月等额偿还。其中住房公积金贷款的最高限额为10万元。如果该家庭以月收入的35%用来支付抵押贷款月还款额,那么此种贷款方案要求该家庭的最低月收入为多少?假设该家庭在按月还款3年后,于第4年初一次性提前偿还商业贷款本金5万元,那么从第4年起该家庭的抵押贷款的月还款额为多少?”相关问题
-
第1题:
某家庭以30万元购买了一套住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,按月等额还款,如果该家庭于第6年初一次提前偿还贷款本金5万元,则从第6年开始的抵押贷款月还款额将减少( )元。
A.544.10
B.555.10
C.1776.32
D.2109.38
正确答案:B
-
第2题:
某家庭以4 000元/m2的价格,购买了一套建筑面积为120 m2的住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,抵押贷款价值比率为70%。如该家庭在按月等额还款5年后,于第6年初一次提前偿还了贷款本金8万元,问从第6年开始的抵押贷款月还款额是多少? 答案:解析:改错如下:
答案:解析:改错如下:
-
第3题:
某家庭以每平方米8000元的单价购买了一套建筑面积为100平方米的住宅用于自住,并向银行申请了个人住房抵押贷款。银行通过对相关材料的审核,确认该家庭为首次购房,并为该家庭提供了贷款总额为总房价的70%,贷款期限为10年,贷款年利率为6%,按月等额偿还的个人住房抵押贷款,其余购房款为该家庭的自付款,该家庭在按月等额还款5年后,于第6年初一次性提前偿还了贷款本金20万元。
根据以上资料,回答下列问题:
该家庭从第6年开始的抵押贷款月还款额为()元。A.2350.59
B.4490.37
C.4623.97
D.5015.06答案:A解析:将所有现金流量均换算到第6年初再进行计算。由81题可知若正常还款每月还款额为6217.15元,则到第6年初尚需还款额为A(P/A,i,n)=6217.15(P/A,0.5%,5×12)=6217.15×[(1+0.5%)5×12-1]/[0.5%×(1+0.5%)5×12]-2=121585.57(元),从第6年开始的抵押贷款月还款额为P(A/P,i,n)=121585.57(A/P,0.5%,5×12)=121585.57×[0.5%×(1+0.5%)5×12]/[(1+0.5%)5×12-1]=2350.59(元)。 -
第4题:
某家庭以每平方米8000元的单价购买了一套建筑面积为100平方米的住宅用于自住,并向银行申请了个人住房抵押贷款。银行通过对相关材料的审核,确认该家庭为首次购房,并为该家庭提供了贷款总额为总房价的70%,贷款期限为10年,贷款年利率为6%,按月等额偿还的个人住房抵押贷款,其余购房款为该家庭的自付款,该家庭在按月等额还款5年后,于第6年初一次性提前偿还了贷款本金20万元。
根据以上资料,回答下列问题:
该家庭向银行申请的个人住房抵押贷款属于()。A.住房公积金贷款
B.商业性贷款
C.组合贷款
D.房地产开发贷款答案:B解析:根据贷款资金来源,把个人住房贷款分为住房公积金贷款、商业性贷款和组合贷款。住房公积金贷款是用住房公积金发放的贷款,带有互助性质,其贷款利率比商业性贷款低。商业性贷款是贷款人以营利为目的的贷款。组合贷款是借款人所需资金先申请住房公积金贷款,不足部分申请商业性贷款,即贷款总金额由住房公积金贷款和商业性贷款两部分组成。 -
第5题:
某家庭以30万元购买了一套住宅,银行为其提供了20年期的住房抵押贷款,该贷款的年利率为9%,按月等额还款,如果该家庭于第6年年初一次提前偿还贷款本金7万元,则从第6年开始的抵押贷款月还款额将减少( )元。A、 544.10
B、 709.99
C、 6300.00
D、 709.38答案:B解析:将第6年年初的7万元看做P,在余下的10年中每月等额还款数就是从第6年开始的抵押贷款月还款额减少值。运用公式

可得:?
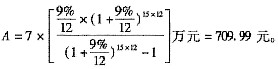
注意:公式中的n是15而不是14,因为第6年年初等于第5年年末。 -
第6题:
某家庭估计在今后10年内的月收入为20000元,如果其月收入的35%可以用来支付住房抵押贷款的月还款额,在年贷款利率为6%的情况下,该家庭有偿还能力的最大抵押贷款额是多少答案:解析:该家庭每月用于住房支出的数额A=20000×35%=7000(元),i=6%/12=0.5%,n=10×12=120(月)。
最高贷款额P=A/i×[1-1/(1+i)n],P=7000/0.5%×[1-1/(1+0.5%)120]=630514.17(元)。 -
第7题:
某家庭以抵押贷款的方式购买了一套价值为30万元的住宅,如果该家庭首付款为房价的20%,其余房款用抵押贷款支付。如果抵押贷款的期限为20年,按月等额偿还,年贷款利率为6%,月还款额为( )元。A、 1655.33
B、 1719.43
C、 1743.69
D、 2149.29答案:B解析:A=P[i(1+i)n)÷[(1+i)n-1)
=300000×80%×[1+0.5%×[(1+0.5%)240]÷[(1+0.5%)240-1)
=1719.43(元) -
第8题:
某家庭以4000元/m2的价格,购买了一套建筑面积为120m2的住宅,银行为其提供了15年期的住宅抵押贷款,该贷款的年利率为6%,抵押贷款价值比率为70%。如该家庭在按月等额还款5年后,于第6年初一次提前偿还了贷款本金8万元,问从第6年开始的抵押贷款月还款额是多少?答案:解析:
第二步,计算出第6年年初(也就是第五年年末)偿还的本金部分,在第6到第15年内减少的月还款额
第三步,计算从第6年开始抵押贷款月还款额
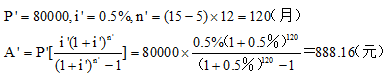
第三步,计算从第6年开始抵押贷款月还款额
-
第9题:
某家庭为购买一套住宅,银行为其提供了15年的住房抵押贷款,贷款额度为196000,该贷款的年利率为6%,月还款常数为0.65%,问: (1)该家庭按等额偿还贷款本息月还款额应为多少? (2)抵押贷款到期后,该家庭应向银行偿还的剩余本金金额是多少?
正确答案: M=196000k=0.65%n=15*12=180月I=6%/12=0.5%
(1)按月等额还款月还款额应为:
A=M*i/[1-(1+i)-n]=196000*0.5%/[1-(1+0.5%)/x7f180]=1653.96元或用A=Mi(1+i)n/[(1+i)n-1]结果相同
(2)实际每月的还款额为:
M*k=196000*0.65%=1274元
借款人每月欠还的本金为:1653.96-1274=379.96元
抵押贷款到期后,该家庭应偿还的剩余本金为:
F=A*[(1+i)n-1]/i=379.96*[(1+0.5%)180-1]/0.5%=110499.30元
*注:等额分付终值公式推导:
F=A+A*(1+i)+…+A*(1+i)n-1=A*(1+(1+i)+…+(1+i)n-1)式1
F*(1+i)=A*((1+i)+…+(1+i)n)式2
式2-式1:F*i=A*((1+i)n-1)
推出F=A*((1+i)n-1)/i
【式1两边同乘(1+i)可得式2】 -
第10题:
计算题:某家庭准备以抵押贷款方式购买一套住房。该家庭月总收入16000元,最多能以月收入的30%支付住房贷款的月还款额。年贷款利率为12%,最长贷款期限20年,最低首付款为房价的30%,若采用按月等额偿还方式, 问: (1)该家庭能购买住房的最高总价是多少?若第五年末,该家庭月收入突增为18000元,第5年末银行贷款利率上调为15%,为保持原月偿还不变,则: (2)该家庭需在第6年初一次性提前偿还贷款多少元? (3)如果不提前偿还贷款,则需将贷款期限延长多少年?
正确答案: (1)计算该家庭购买住房的最高总价
月还款额:A=16000×30%=4800(元)(0.5分)
最高贷款额:P=A/i[1-1/(1+i)n]=4800/(1%)[1-1/(1+1%)240]=435933.20(元)=43.59(万元)
(本步计算中,i取1%,n取240,给0.5分)
购买住房的最高总价:43.59/70%=62.27(万元)(0.5分)
(2)计算第6年初一次性提前偿还款
解法一:
第5年末尚余贷款本金:
P’=A/i[1-1/(1+i)n']=4800/(1%)[1-1/(1+1%)180]=399943.99(元)=39.99万元
(本步计算中,i取1%,n′取180,给0.5分)
调息后的月还款额:
A’=P’[〖i'(1+i')〗n'/(〖(1+i')〗n'-1)]=399943.99×〖1.25%(1+1.25%)〗180/(〖(1+1.25%)〗180-1)=5597.56(1分)
(本步计算中,i′取1.25%,n′取180,给0.5分)
调息后每月增加的还款额:5597.56-4800=797.56(元)(0.5分)
提前还款额:
P”=797.56/(1.25%)[1-1/(1+1.25%)180]=56985.38(元)=5.70(万元)(1分)
解法二:
设提前还款额为P″,则有
A/i'[1-1/〖(1+i')〗n']+p"=p'(1分)
第5年未尚余贷款本金:
P’=A/i[1-1/(1+i)n']=4800/(1%)[1-1/(1+1%)180]=399943.99(元)=39.99万元(1分)
P”=P’-A/i'[1-1/(1+i')n']=399943.99-4800/(1.25%)[1-1/(1+1.25%)180](1分)=56985.70(元)=5.7(万元)(0.5分)
(3)贷款延长期的计算
设从第5年末开始的还款期为X月,则有
P’=A/i'[1-1/(1+i')x](0.5分)
399943.99=5400/1.25%[1-1/(1+1.25%)x](0.5分)
x=209.35(月)(0.5分)
延长期:209.35-180=19.35(月)≈1.6(年)(0.5分) -
第11题:
问答题【例5-3】某家庭预计在今后10年内的月收入为16000元,如果其中的30%可用于支付住房抵押贷款的月还款额,年贷款利率为12%,问该家庭有偿还能力的最大抵押贷款申请额是多少?正确答案:解析: -
第12题:
问答题【例5-6】某家庭拟购买一套面积为80m2的经济适用住宅,单价为3500元/㎡,首付款为房价的25%,其余申请公积金和商业组合抵押贷款。已知公积金和商业贷款的利率分别为4.2%和6.6%,期限均为15年,公积金贷款的最高限额为10万元。问该家庭申请组合抵押贷款后的最低月还款额是多少?正确答案:解析: -
第13题:
某家庭以30万元购买一套住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,按月等额还款。如果该家庭于第6年初一次提前偿还贷款本金5万元。则从第6年开始的抵押贷款月还款额将减少()元。A:544.10
B:556.00
C:1776.32
D:2109.38答案:B解析:具体计算过程如下:①n1=15*12=180个月,n2=5*12=60个月,i=6%/12=0.5%;②初始抵押贷款数额为30万元,③该家庭月还本付息额为:A=P*i/[1-(1+i)-n]=30*05%/[1-(1+0.5%)-180]=0.2530(万元),④第6年初尚未偿还折抵押贷款本金额为:P=(A/i)*[1-(1+1)-n]=(0.2530/0.5%)*[1-(1+0.5%)-(180-60)]=22.77(万元);⑤当该家庭在第6年初一次偿还本金5万元后,则在第6年初尚未偿还抵押贷款本金数额为22.77-5=17.77(万元),⑥从第6年开始该家庭月还本付息额为:A1=P1*i/[1-(1+i)-n]=17.77*0.5%/[1-(1+0.5%)-120]=0.1974(万元);⑦从第6年开始的月还本付息额将减少:2530-1974=556(元)。 -
第14题:
某家庭预购买一套面积为80 m2的经济适用住宅,单价为3500元/m2,首付款为房价的25%,其余申请公积金和商业组合抵押贷款。已知公积金和商业贷款的利率分别为4. 2%和6.6%,期限均为15年,公积金贷款的最高限额为10万元。问该家庭申请组合抵押贷款后的最低月还款额是多少? 答案:解析:改错如下:
答案:解析:改错如下:
(1)计算等额偿还公积金贷款和商业贷款本息的月还款额: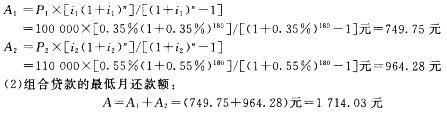
-
第15题:
某家庭以每平方米8000元的单价购买了一套建筑面积为100平方米的住宅用于自住,并向银行申请了个人住房抵押贷款。银行通过对相关材料的审核,确认该家庭为首次购房,并为该家庭提供了贷款总额为总房价的70%,贷款期限为10年,贷款年利率为6%,按月等额偿还的个人住房抵押贷款,其余购房款为该家庭的自付款,该家庭在按月等额还款5年后,于第6年初一次性提前偿还了贷款本金20万元。
根据以上资料,回答下列问题:
该家庭在贷款期限前5年抵押贷款的月还款额为()元。A.6217.15
B.8357.29
C.8490.53
D.8881.62答案:A解析:
-
第16题:
某家庭以2000元/m2的价格,购买了一套建筑面积为120m2的住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,抵押贷款价值比率为70%。如该家庭在按月等额还款5年后,于第6年初一次提前偿还了贷款本金4万元,那么从第6年开始的抵押贷款月还款额为( )元。A.1417.68
B.444.08
C.1861.76
D.973.60答案:D解析:本题考查的是复利计算。参见教材P158。
1.计算出贷款额
1)房屋总价:2000×120=24(万元)
2)贷款额:24×70%=16.8(万元)
2.计算出月供
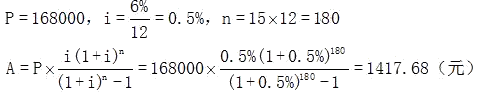
3.第6年初一次偿还本金4万元,则在6-15年间减少的月供为
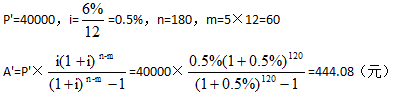
4.提前还款后的月供
1417.68-444.08=973.6(元) -
第17题:
某家庭以80万元购买了一套住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,按月等额还款,如果该家庭于第6年初一次提前偿还贷款本金10万元,则从第6年开始的抵押贷款月还款额将减少( )元。A、1110.21
B、1244.10
C、1776.32
D、2109.38答案:A解析:本题考查的是复利系数的应用。将第6年初的10万元看作P,在余下的10年中每月等额还款数就是从第6年开始的抵押贷款月还款额减少值。月利率=6%÷12=0.5%,运用公式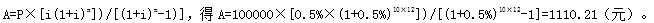
-
第18题:
某家庭以抵押贷款的方式购买了一套价值为100万元的住宅,首付款为房价的50%,其余房款用抵押贷款支付。如果抵押贷款的期限为20年,按月等额偿还,年贷款利率为12%,问:
(1)抵押贷款额、月贷款利率与月还款额各为多少
(2)如果该家庭30%的收入可以用来支付抵押贷款月还款额,则该家庭须月收入多少,才能购买上述住宅
(3)如果该家庭在按月等额还款5年后,于第6年年初一次提前偿还剩余贷款本息,则还款额为多少答案:解析:(1)抵押贷款额P=100×50%=50万元;
月贷款利率i=12%/12=1%;
月还款额为:A=P×i(1+i)n/[(1+i)n-1]=50×1%(1+1%)240/[(1+1%)240-1]=0.550543万元=5505.43元;
(2)该家庭欲购买上述住宅,其月收入须为:5505.43/30%=18351.43元
(3)该家庭在第6年年初一次提前偿还剩余贷款余额时,所需偿还金额为
Pn=A[((1+i)n-m-1)/[i(1+i)n-m],其中,n=12×20=240,m=12×5=60,
代入数据,得到Pn=5505.43×[((1+1%)240-60-1)/[1%(1+1%)240-60]=458721.59元=45.87万元。 -
第19题:
王某购买一套商品住宅,成交价格为50万元,首期付款为房价的30%,余款向银行抵押贷款。该贷款的贷款期限为10年,贷款年利率为6%,采用按月等额还款方式偿还。若第6年年初王某决定提前偿还全部贷款余额,此时的贷款余额为多少元?
2、某投资者以8000万元购入一写字楼物业20年的使用权用于出租经营,已知该投资者的目标收益率为27%,预计未来20年内的年租金上涨率为10%,问该写字楼于第八年的净租金收入为多少时,方能满足投资者收益目标的要求?
3、某家庭拟购买一套新房,并将原有住房出租。预计原有住房的净租金收入为每月2000元,资本化率为9.6%,假设租金和住房市场价值不随时间发生变化。该家庭希望实现以租养房,即每月的抵押贷款还款额不超过原有住房的租金收入。购买新房的最低首付款为房价的30%,余款申请年利率为6%的住房抵押贷款,按月等额还款,最长贷款年限为20年。问:
(1)该家庭能够购买最高总价为多少万元的新房(精确到小数点后2位)?
(2)设该家庭购买了这一最高总价的新房,并希望在还款一段时间之后,利用出售原有住房的收入一次性提前还清抵押贷款,问至少需要在还款多少个月(取整)后,再出售原有住房并还清贷款?
4、某投资者以3.8万元/m2的价格购买了一个建筑面积为80m2的店铺,用于出租经营。该投资者以自有资金支付了总价款的30%,其余用银行提供的抵押贷款支付。该抵押贷款期限为10年,年利率为5.31%基础上上浮2个百分点,按年等额偿还。经营费用为毛租金收入的25%。投资者希望该店铺投资在抵押贷款还贷期内的税前现金回报率不低于10%。试计算在还贷期内满足投资者最低现金回报率要求的月租金单价(每平方米建筑面积月毛租金)。
5、某家庭以抵押贷款的方式购买了一套价值为100万元的住宅,首付款为房价的50%,其余房款用抵押贷款支付。如果抵押贷款的期限为20年,按月等额偿还,年贷款利率为12%,问:
(1)抵押贷款额、月贷款利率与月还款额各为多少?
(2)如果该家庭30%的收入可以用来支付抵押贷款月还款额,则该家庭须月收入多少,才能购买上述住宅?
(3)如果该家庭在按月等额还款5年后,于第6年年初一次提前偿还剩余贷款本息,则还款额为多少?
6、某家庭准备以抵押贷款方式购买一套住房。该家庭月总收入7000元,最多能以月总收入的25%支付住房贷款的月还款额。年贷款利率为6%,最长贷款期限20年。最低首付款为房价的30%,若采用按月等额偿还方式。
<1> 、该家庭能购买此房的最高总价是多少?
<2> 、若第5年末银行贷款利率上调为9%,为保持原月偿还额不变。则该家庭需在第6年初一次性提前偿还贷款多少元?
<3> 、如果不提前偿还贷款,则需将贷款期限延长多少年?答案:解析:1、
贷款余额=第6年至第10年的年值,折现到第6年年初(第5年年末)时的现值。
第一步,已知贷款P,先求出月还款额A
P=50×(1-30%)=35(万元)=350000(万元)
i月=6%/12=0.5%,n=10×12=120
A=P×i(1+i)n/[(1+i)n-1]=350000×0.5% (1+0.5%)120/[(1+0.5%)120-1]=3886(元)
第二步,把第六年到第十年的年值(月供),折现到第6年年初(第5年年末)
已知n=10×12=120,m=5×12=60,n-m=60
Pn=A[((1+i)n-m-1)/[i(1+i)n-m]=3886[((1+0.5%)60-1)/[0.5%(1+0.5%)60]=201006(元)=20.1(万元)
2、
(1)已知P=8000万元,n=20年,i=27%,s=10%,t=8
(2)由A1=P×(i-s)/(1-[(1+s)/(1+i)]n)可得:
A1=8000×(27%-10%)/{1-[(1+10%)/(1+27%)]20)=1441.4(万元)
(3)利用公式At=A1(1+s)t-1,可得A8=1441.4×(1+10%)8-1=2808.9(万元)
该写字楼第八年的净租金收入达到2808.9万元以上时,方能满足投资者收益目标的要求。
3、
1.计算出月供对应的现值
A=2000元,i=6%/12=0.5%,n=20×12=240(月)
P=A/i[1-1/(1+i)n]=2000/0.5%[1-1/(1+0.5%)240]=279161.5(元)
2.能购买新房的最高价:27.92/(1-30%)=39.87(万元)
1)因为题中并未告诉我们原有住房还有多长的收益时间,所以我们只能采用无限年限的A-P求出原有房屋的价值(收益法)
V=A/r=2000×12/9.6%=25(万元)
2)设至少应还款n月,再提前还款
将240-n个月的月供,折现到提前还款时间,其现值应为25万元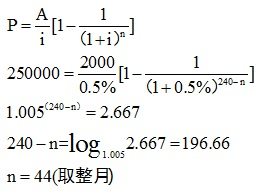
4、
解法一:
购买商铺总投资:38000×80=3040000(元)
购买商铺首付款(初始投资、自有资金、权益投资):
3040000×30%=912000(元)
购买商铺的贷款额(P):
3040000×70%=2128000(元)
抵押贷款年还本付息额:
i=2%+5.31%=7.31%,n=10年
A=P×i(1+i)n/[(1+i)n-1]
=2128000×7.31%×(1+7.31%)10/[(1+7.31%)10-1]
=307335.47(元)
净经营收入(利用现金回报率):
(净经营收入-年还本付息额)/首付款=10%
所以:净经营收入=首付款×10%+年还本付息额=912000×10%+307335.47=398535.47(元)
毛租金收入=净经营收入+经营费用=398535.47+毛租金收入×25%
则:毛租金收入=398535.47/(1-25%)=531380.63(元)
最低月租金单价=毛租金收入/(可出租面积×12个月)=531380.63/(80×12)=553.52(元/m2/月)
解法二:
(1)购买总价:3.8×80=304(万元)
(2)自有资金:304×30%=91.2(万元)
(3)抵押贷款年等额偿还额:
抵押贷款总额:304×70%=212.8(万元)
已知:n=10年,i=5.31%+2%=7.31%
则:A=P×i(1+i)n/[(1+i)n-1]=2128000×7.31%×(1+7.31%)10/[(1+7.31%)10-1]=307335.47(元)
(4)设月租金单价为Y元/(m2/月)
年租金:80×12Y=960Y
年税前现金流:960Y-960Y×25%-307335.47
则:(960Y-960Y×25%-307335.47)/912000×100%=10%
则:Y=553.52(元/m2)
5、
(1)抵押贷款额P=100×50%=50(万元)
月贷款利率i=12%/12=1%;
月还款额为:A=P×i(1+i)n/[(1+i)n-1]=50×1%(1+1%)240/[(1+1%)240-1]=0.550543万元=5505.43(元)
(2)该家庭欲购买上述住宅,其月收入须为:5505.43/30%=18351.43(元)
(3)该家庭在第6年年初一次提前偿还剩余贷款余额时,所需偿还金额为
Pn=A[((1+i)n-m-1)/[i(1+i)n-m],其中,n=12×20=240,m=12×5=60,
代入数据,得到Pn=5505.43×[((1+1%)240-60-1)/[1%(1+1%)240-60]=458721.59元=45.87(万元)
6、
(1)月还款额:7000×25%=1750(元)
(2)最高贷款额(A-P)
A=1750,i=6%/12 =0.5%,n=20×12=240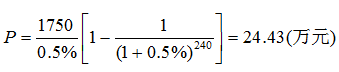
(3)购买房屋的最高总价:24.43÷70%=34.9(万元)
(1)为保证每期还款不变,仍为1750元,则必须延长还款期限。
设延长后的还款期限为m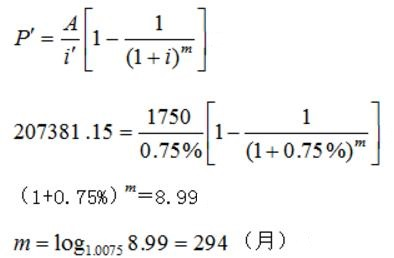
(2)延长还款期294-180=114(月)=9.5(年) -
第20题:
某家庭以2000元/m2的价格,购买了一套建筑面积为120m2的住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,抵押贷款价值比率为70%。如该家庭在按月等额还款5年后,于第6年初一次提前偿还了贷款本金4万元,那么从第6年开始的抵押贷款月还款额为( )元。A.1417.68
B.444.08
C.1861.76
D.973.60答案:D解析:本题考查的是资金等效值的换算。

-
第21题:
某家庭预购买一套面积为100m2的经济适用住宅,单价为3875元/m2,首付款为房价的20%,其余申请公积金和商业组合抵押贷款。已知公积金和商业贷款的利率分别为4.2%和6.6%,期限均为15年,公积金贷款的最高限额为20万元。问该家庭申请组合抵押贷款后的最低月还款额是()元。
- A、1499.5
- B、2463.78
- C、1928.56
- D、3428.06
正确答案:B -
第22题:
问答题【例5-7】某家庭以4000元/㎡的价格,购买了一套建筑面积为120㎡的住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,抵押贷款价值比率为70%。如该家庭在按月等额还款5年后,于第6年初一次提前偿还了贷款本金8万元,问从第6年开始的抵押贷款月还款额是多少?正确答案:解析: -
第23题:
问答题计算题:某家庭准备以抵押贷款方式购买一套住房。该家庭月总收入16000元,最多能以月收入的30%支付住房贷款的月还款额。年贷款利率为12%,最长贷款期限20年,最低首付款为房价的30%,若采用按月等额偿还方式, 问: (1)该家庭能购买住房的最高总价是多少?若第五年末,该家庭月收入突增为18000元,第5年末银行贷款利率上调为15%,为保持原月偿还不变,则: (2)该家庭需在第6年初一次性提前偿还贷款多少元? (3)如果不提前偿还贷款,则需将贷款期限延长多少年?正确答案: (1)计算该家庭购买住房的最高总价
月还款额:A=16000×30%=4800(元)(0.5分)
最高贷款额:P=A/i[1-1/(1+i)n]=4800/(1%)[1-1/(1+1%)240]=435933.20(元)=43.59(万元)
(本步计算中,i取1%,n取240,给0.5分)
购买住房的最高总价:43.59/70%=62.27(万元)(0.5分)
(2)计算第6年初一次性提前偿还款
解法一:
第5年末尚余贷款本金:
P’=A/i[1-1/(1+i)n']=4800/(1%)[1-1/(1+1%)180]=399943.99(元)=39.99万元
(本步计算中,i取1%,n′取180,给0.5分)
调息后的月还款额:
A’=P’[〖i'(1+i')〗n'/(〖(1+i')〗n'-1)]=399943.99×〖1.25%(1+1.25%)〗180/(〖(1+1.25%)〗180-1)=5597.56(1分)
(本步计算中,i′取1.25%,n′取180,给0.5分)
调息后每月增加的还款额:5597.56-4800=797.56(元)(0.5分)
提前还款额:
P”=797.56/(1.25%)[1-1/(1+1.25%)180]=56985.38(元)=5.70(万元)(1分)
解法二:
设提前还款额为P″,则有
A/i'[1-1/〖(1+i')〗n']+p"=p'(1分)
第5年未尚余贷款本金:
P’=A/i[1-1/(1+i)n']=4800/(1%)[1-1/(1+1%)180]=399943.99(元)=39.99万元(1分)
P”=P’-A/i'[1-1/(1+i')n']=399943.99-4800/(1.25%)[1-1/(1+1.25%)180](1分)=56985.70(元)=5.7(万元)(0.5分)
(3)贷款延长期的计算
设从第5年末开始的还款期为X月,则有
P’=A/i'[1-1/(1+i')x](0.5分)
399943.99=5400/1.25%[1-1/(1+1.25%)x](0.5分)
x=209.35(月)(0.5分)
延长期:209.35-180=19.35(月)≈1.6(年)(0.5分)解析: 暂无解析
