名师备选题库(一)

B.
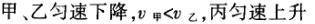
C.

D.
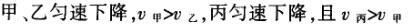

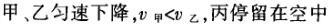
B.
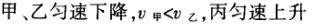
C.
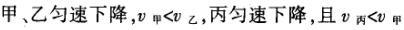
D.
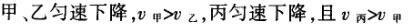

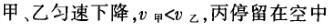
B.
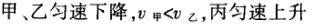
C.

D.
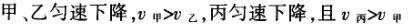

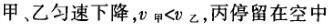
B.
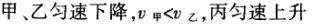
C.
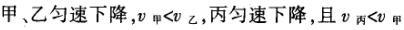
D.


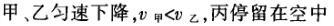
B.
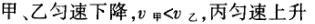
C.
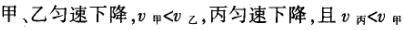
D.
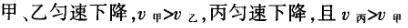

1甲、乙、丙三人各乘一架直升飞机,甲看到楼房匀速上升,乙看到甲机匀速上升,丙看到乙机匀速下降,甲看到丙机匀速上升,则甲、乙、丙相对于地面的运动不可能是()A甲、乙匀速下降,v乙v甲,丙机停在空中B甲、乙匀速下降,v乙v甲,丙机匀速上升C甲、乙匀速下降,v乙v甲,丙机匀速下降,v丙v甲D甲、乙匀速下降,v乙v甲,丙机匀速下降,v丙v甲解析:选D.甲和乙在匀速下降,但乙的下降速度更大丙则有几种情况:可能是停在空中,也可能匀速上升,还可能是匀速下降,但下降的速度比甲的要小故正确答案为D.2(2012江苏无锡模拟)历史上有些科学家曾把在相等位移内速度变化相等的单向直线运动称为“匀变速直线运动”(现称“另类匀变速直线运动”),“另类加速度”的定义为Aeq f(vtv0,s),其中v0和 vt分别表示某段位移s内的初速和末速A0表示物体做加速运动A0且保持不变,则a逐渐变小C若A不变,则物体在中间位置处的速度为eq f(v0vt,2)D若A不变,则物体在中间位置处的速度为 eq r(f(voal(2,0)voal(2,t),2)解析:选C.题干中两式联立得,Asat,若相等位移内A不变,则at的乘积不变,故选项A错误;若A0且保持不变,则vtv0,故后面完成相等的位移所用时间t越小,由at乘积不变可知a逐渐变大,选项B错误,若A不变,设物体在中间位置处的速度为veq f(s,2),则Aeq f(vf(s,2)v0,s/2)eq f(vtvf(s,2),s/2),解得veq f(s,2)eq f(v0vt,2),故选项C正确,而D错误3.如图,两个光滑的斜面高度相同,右边由两部分组成,且ABBCAD,两小球a、b分别从A点沿左右两侧面由静止下滑,不计转折处的能量损失,两次下滑时间分别为t1与t2,则()At1t2Bt1t2Ct1t2 D无法判断解析:选A.做出vt图象可得答案是A.4A、B两辆汽车在笔直的公路上同向行驶当 B车在A车前84 m处时,B车速度为4 m/s,且正以2 m/s2的加速度做匀加速运动;经过一段时间后,B车加速度突然变为零A车一直以20 m/s的速度做匀速运动经过12 s后两车相遇问B车加速行驶的时间是多少?解析:设A车的速度为vA,B车加速行驶时间为t,两车在t0时相遇则有sAvAt0sBvBteq f(1,2)at2(vBat)(t0t)式中,t0 12 s,sA、sB分别为 A、B两车相遇前行驶的路程依题意有sAsBs式中s84 m.由式得t22t0teq f(2vBvAt0s,a)0代入题给数据vA20 m/s,vB4 m/s,a 2 m/s2,有t224t1080式中t的单位为s.解得t16 s,t218 st218 s不合题意,舍去因此,B车加速行驶的时间为 6 s.答案:6 s5已知O、A、B、C为同一直线上的四点,AB间的距离为l1,BC间的距离为l2,一物体自O点由静止出发,沿此直线做匀加速运动,依次经过A、B、C三点,已知物体通过AB段与BC段所用的时间相等求O与A的距离解析:设物体的加速度为a,到达A的速度为v0,通过AB段和BC段所用的时间为t,则有l1v0teq f(1,2)at2l1l22v0t2at2联立式得l2l1at23l1l22v0t设O与A的距离为l,则有leq f(voal(2,0),2a)联立式得leq f(3l1l22,8l2l1).答案:eq f(3l1l22,8l2l1)6甲、乙两运动员在训练交接棒的过程中发现:甲经短距离加速后能保持9 m/s的速度跑完全程;乙从起跑后到接棒前的运动是匀加速的为了确定乙起跑的时机,需在接力区前适当的位置设置标记在某次练习中,甲在接力区前s013.5 m处作了标记,并以v9 m/s的速度跑到此标记时向乙发出起跑口令乙在接力区的前端听到口令时起跑,并恰好在速度达到与甲相同时被甲追上,完成交接棒已知接力区的长度为L20 m求:(1)此次练习中乙在接棒前的加速度a;(2)在完成交接棒时乙离接力区末端的距离解析:(1)设经过时间t,甲追上乙,则根据题意有vtvt/213.5将v9 m/s代入得到:t3 s,再由vat解得:a3 m/s2.(2)在追上乙的时候,乙跑的距离为s,则:sat2/2代入数据得到s13.5 m所以乙离接力区末端的距离为sLs20 m
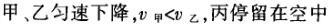
B.
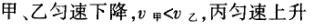
C.
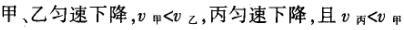
D.
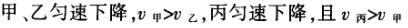

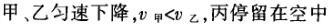
B.
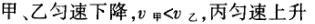
C.
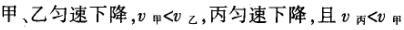
D.
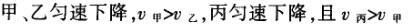

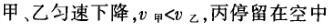
B.
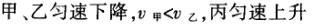
C.
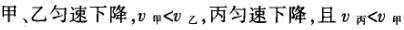
D.
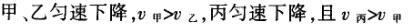

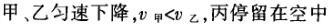
B.

C.
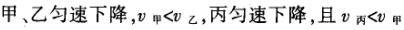
D.
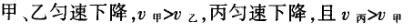

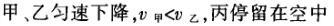
B.
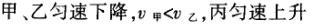
C.
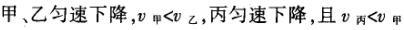
D.