自学考试专题:全国1010自学考试线性代数试题
A.对称矩阵
B.可逆矩阵
C.n阶矩阵的转置矩阵
D.线性方程组的系数矩阵
在数学上表示一个横成行、纵成列的数字方阵的是
A、方阵
B、队列
C、矩阵
D、数组
E、行列式
B、 秩为r的矩阵中,所有r阶子式均不为零
C、 若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零
D、 秩为r的矩阵中,不存在等于零的r-1阶子式
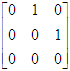
中存在等于0的1阶子式。
B、 秩为r的矩阵中,所有r阶子式均不为零
C、 若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零
D、 秩为r的矩阵中,不存在等于零的r-1阶子式

中存在等于0的1阶子式。
 ,请计算
,请计算


全国2010年10月自学考试线性代数试题课程代码:02198说明:在本卷中,AT表示矩阵A的转置矩阵,A*表示矩阵A的伴随矩阵,E是单位矩阵,|A|表示方阵A的行列式,r(A)表示矩阵A的秩.一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。错选、多选或未选均无分。1设矩阵A=,B=(1,1)则AB=( )A0B(1,-1)CD2设A为3阶矩阵,|A|=1,则|-2AT|=( )A-8B-2C2D83设行列式D1=,D2=,则D1=( )A0BD2C2D2D3D24设矩阵A的伴随矩阵A*,则A-1=( )ABCD5设A,B均为n阶可逆矩阵,则必有( )AA+B可逆BAB可逆CA-B可逆DAB+ BA可逆6设A为3阶矩阵且r(A)=2,B=,则r(AB)=( )A0B1C2D37设向量组1=(1,2),2=(0,2),=(4,2),则( )A1,2,线性无关B不能由1,2线性表示C可由1,2线性表示,但表示法不惟一D可由1,2线性表示,且表示法惟一8设齐次线性方程组有非零解,则为( )A-1B0C1D29设A为3阶实对称矩阵,A的全部特征值为0,1,1,则齐次线性方程组(E-A)x=0的基础解系所含解向量的个数为( )A0B1C2D310二次型f(x1,x2,x3)=x12+x22+4x32-2tx2x3正定,则t满足( )A-4t-2B-2 t 2C2t4Dt4二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。错填、不填均无分。11行列式的值为_.12已知A=,则|A|中第一行第二列元素的代数余子式为_.13设A,B都是3阶矩阵,且|A|=2,B=-2E,则|A-1B|=_.14设矩阵A=,P=,则AP3=_.15已知向量组1=(1,2,3),2=(3,-1,2),3=(2,3,k)线性相关,则数k=_.16已知Ax=b为4元线性方程组,r(A)=3. 1,2,3为该方程组的3个解,且1=,2+3=,则该线性方程组的通解是_.17设2是矩阵A的一个特征值,则矩阵3A必有一个特征值为_.18已知P是3阶正交矩阵,向量=, =,则内积(P,P)=_.19与矩阵A=相似的对角矩阵为_.20二次型f(x1,x2,x3)=2x1x2+2x1x3的秩为_.三、计算题(本大题共6小题,每小题9分,共54分)21求行列式D=的值.22设矩阵A=,B=,求满足矩阵方程XA-B=2E的矩阵X.23设向量组1=(1,3,0,5)T,2=(1,2,1,4)T,3=(1,1,2,3)T,4=(1,0,3,k)T,确定k的值,使向量组1,2,3,4的秩为2,并求该向量组的一个极大线性无关组.24当数a为何值时,线性方程组有无穷多解?并求出其通解.(要求用它的一个特解和导出组的基础解系表示)25已知3阶矩阵A的特征值为-1,1,2,设B=A2+2A-E,求(1)矩阵A的行列式及A的秩.(2)矩阵B的特征值及与B相似的对角矩阵.26求二次型f(x1,x2,x3)=-4x1x2+2x1x3+2x2x3经可逆线性变换所得的标准形.四、证明题(本题6分)27已知n阶矩阵A,B满足A2=A,B2=B及(A-B)2=A+B,证明AB=0.第 4 页
 ,请计算
,请计算


B、 秩为r的矩阵中,所有r阶子式均不为零
C、 若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零
D、 秩为r的矩阵中,不存在等于零的r-1阶子式

中存在等于0的1阶子式。
 ,请计算
,请计算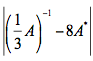


B、 秩为r的矩阵中,所有r阶子式均不为零
C、 若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零
D、 秩为r的矩阵中,不存在等于零的r-1阶子式

中存在等于0的1阶子式。
B、 秩为r的矩阵中,所有r阶子式均不为零
C、 若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零
D、 秩为r的矩阵中,不存在等于零的r-1阶子式

中存在等于0的1阶子式。
更多 “自学考试专题:全国1010自学考试线性代数试题” 相关考题
相关内容
最新试卷
热门试卷
- 磺化工艺作业安全生产考试试题测试强化卷及答案(69)-
- 磺化工艺作业安全生产考试试题测试强化卷及答案(51)-
- 2022造价工程师《工程计价》真题(全考点)模拟卷及参考答案【46】-
- 2022造价工程师《工程计价》真题(全考点)模拟卷及参考答案【31】-
- 华中科技大学硕士研究生入学考试《基础英语》考试大纲-
- 2013年湖北省宜昌市初中毕业生学业考试语文试题-
- 烟花爆竹经营单位-主要负责人安全生产考试试题测试强化卷及答案79-
- 2022年重庆市安全员B证考试题库试题测试强化卷及答案[45]-
- 2022年重庆市安全员B证考试题库试题测试强化卷及答案[52]-
- 2022年重庆市安全员B证考试题库试题测试强化卷及答案78-
