自学考试专题:全国0904自学考试线性代数试题
在数学上表示一个横成行、纵成列的数字方阵的是( )
A.方阵
B.趴列
C.矩阵
D.数组
E.行列式
在数学上表示一个横成行、纵成列的数字方阵的是
A、方阵
B、队列
C、矩阵
D、数组
E、行列式
B、 秩为r的矩阵中,所有r阶子式均不为零
C、 若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零
D、 秩为r的矩阵中,不存在等于零的r-1阶子式
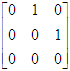
中存在等于0的1阶子式。
 ,求 ①二次型
,求 ①二次型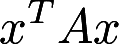 的标准形; ②行列式
的标准形; ②行列式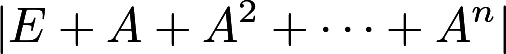 的值,其中E为单位矩阵
的值,其中E为单位矩阵
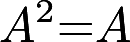 ,求 ①二次型
,求 ①二次型 的标准形; ②行列式
的标准形; ②行列式 的值,其中E为单位矩阵
的值,其中E为单位矩阵
全国2009年4月自学考试线性代数试题课程代码:02198说明:在本卷中,AT表示矩阵A的转置矩阵,A*表示矩阵A的伴随矩阵,E表示单位矩阵,表示方阵A的行列式,r(A)表示矩阵A的秩。一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。错选、多选或未选均无分。13阶行列式中元素a21的代数余子式A21=()A-2B-1C-1D22设n阶可逆矩阵A、B、C满足ABC=E,则B-1=()AA-1C-1BC-1A-1CACDCA3设3阶矩阵A=,则A2的秩为()A0B1C2D34设矩阵A=,B=,P1=,P2=,则必有()AP1P2A=BBP2P1A=BCAP1P2=BDAP2P1=B5设向量组1, 2, 3, 4线性相关,则向量组中()A必有一个向量可以表为其余向量的线性组合B必有两个向量可以表为其余向量的线性组合C必有三个向量可以表为其余向量的线性组合D每一个向量都可以表为其余向量的线性组合6设1, 2, 3, 4是一个4维向量组,若已知4可以表为1, 2, 3,的线性组合,且表示法惟一,则向量组1, 2, 3, 4的秩为()A1B2C3D47设1, 2, 3是齐次线性方程组Ax=0的一个基础解系,则下列解向量组中,可以作为该方程组基础解系的是()A1, 2, 1+2B1, 2, 1-2C1+2, 2+3, 3+1D1-2,2-3,3-18设A为3阶矩阵,且=0,则A必有一个特征值为()A-B-CD9设实对称矩阵A=,则3元二次型f(x1,x2,x3)=xTAx的规范形为()A+B+-C+D-10设2元二次型f(x1,x2)=xTAx正定,则矩阵A可取为()ABCD二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。错填、不填均无分。11.设3阶行列式D3的第2列元素分别为1,-2,3,对应的代数余子式分别为-3,2,1,则D3=_。12.已知3阶行列式=6,则=_。13.设A=,则A2-2A+E=_。14.设A为2阶矩阵,将A的第2列的(-2)倍加到第1列得到矩阵B.若B=,则A=_。15.设3阶矩阵A=,则A-1=_。16.设向量组a1=(a,1,1),a2=(1,-2,1),a3=(1,1,-2),线性相关,则数a=_。17.3元齐次线性方程组的基础解系中所含解向量的个数为_。18.已知3阶矩阵A的特征值为0,-2,3,且矩阵B与A相似,则=_。19.设2阶实对称矩阵A的特征值为1,2,它们对应的特征向量分别为1=(1,1)T,2=(1,k)T,则数k=_。20.二次型f(x1,x2,x3)=(x1-x2)2+(x2-x3)2的矩阵A=_。三、计算题(本大题共6小题,每小题9分,共54分)21.计算4阶行列式.22.设2阶矩阵A=,P=,矩阵B满足关系式PB=A*P,计算行列式.23.求向量组1=(1,1,1,3)T,2=(-1,-3,5,1)T,3=(3,2,-1,4)T,4=(-2,-6,10,2)T的一个极大无关组,并将向量组中的其余向量用该极大无关组线性表示.24.设3元齐次线性方程组(1)确定当a为何值时,方程组有非零解;(2)当方程组有非零解时,求出它的基础解系和全部解.25.设矩阵B=,(1)判定B是否可与对角矩阵相似,说明理由;(2)若B可与对角矩阵相似,求对角矩阵和可逆矩阵P,使P-1BP=.26.设3元二次型f(x1,x2,x3)=+-2x1x2-2x2x3,求正交变换x=Py,将二次型化为标准形.四、证明题(本大题6分)27.设矩阵A=,其中a1,a2,a3互不相同,证明:与A可交换的矩阵只能为对角矩阵.第 4 页
B、 秩为r的矩阵中,所有r阶子式均不为零
C、 若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零
D、 秩为r的矩阵中,不存在等于零的r-1阶子式

中存在等于0的1阶子式。
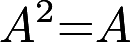 ,求 ①二次型
,求 ①二次型 的标准形; ②行列式
的标准形; ②行列式 的值,其中E为单位矩阵
的值,其中E为单位矩阵
B、 秩为r的矩阵中,所有r阶子式均不为零
C、 若n阶方阵A的秩小于n,则该矩阵A的行列式必等于零
D、 秩为r的矩阵中,不存在等于零的r-1阶子式

中存在等于0的1阶子式。
B.一个图的邻接矩阵表示是唯一的,邻接表表示也唯一
C.一个图的邻接矩阵表示是唯一的,邻接表表示不唯一
D.一个图的邻接矩阵表示不唯一的,邻接表表示是唯一
B.一个图的邻接矩阵表示是唯一的,邻接表表示也唯一
C.一个图的邻接矩阵表示是唯一的,邻接表表示不唯一
D.一个图的邻接矩阵表示不唯一的,邻接表表示是唯一
更多 “自学考试专题:全国0904自学考试线性代数试题” 相关考题
相关内容
最新试卷
热门试卷
- 2021年4月11日陕西事业单位招聘考试《职业能力倾向测试》(综合岗)试题_
- 2021年5月福建省事业单位联考《综合基础知识》试题(网友回忆版)含答案_
- 2021年4月17日江苏事业单位考试《综合知识和能力素质》(管理岗客观题)_
- 2020年浙江省宁波市鄞州区事业单位考试《综合知识》试题(考生回忆版)_
- 2020年山西省高平市事业单位《公共基础知识》试题含答案解析_
- 2020年湖南省永州市直事业单位笔试试题(考生回忆版)含解析答案_
- 2020年12月12日重庆市万州区事业单位考试《综合基础知识》试题含答案解析_
- 2020年9月重庆市璧山区事业单位考试《综合基础知识》试题含答案和解析_
- 2020年8月湖南省长沙市区员额人员招聘考试题含答案和解析_
- 2022年广西省安全员B证考试题库试题(全考点)模拟卷及参考答案(第87次)-
