广东省华南师大附中2007—2008学年度高三综合测试(三)数学试题(理科)
若已知一个栈的进栈序列是1,2,3,,n,其输出序列为p1,p2,p3,?,pn,若p1=n,则pi为()。
A.i
B.n-i
C.n-i+1
D.不确定
若已知一个栈的入栈序列是1,2,3,......,n,其输出序列为p1,p2,p3,..,pn,若p1=n-1,则pi可能为()
A.n
B.n-i
C.n-i+1
D.不确定
若已知一个栈的入栈序列是1、2、3、…、n,其输出序列是p1、p2、p3、…、pn,则加为( )。
A.i
B.n-i
C.n-i+1
D.不确定
解析:栈是一种特殊的线性表,只能在固定的一端进行插入和删除操作。栈的运算是一种后进先出的操作原则。本题中,入栈序列与输出序列的倒置是对应的,即输出序列的P1对应入栈序列的 n,输出序列的p2对应入栈序列的n-1,由此可推出,加pi应入栈序列的n-i+1。
A.i
B.n-i
C.n-i+1
D.不确定
若已知一个栈的进栈序列是l,2,3…n,其输出序列是P1,P2,P3,…PN,若P1=3,则P2为()。
A.可能是2
B.一定是2
C.可能是1
D.一定是1
1广东省华南师大附中 20072008 学年度高三综合测试(三)数学试题(理科)1已知命题 p: ,则 (C )1 B :x 1 D2已知函数 ,则 a 的所有可能值组成的集合为1)(0,1)n()(2 若1 B C D1 , 2,1223命题 p:若 的充分不必要条件;1|, 则命题 q:函数 ,则 ( A ),3),(|1| 定 义 域 是 “p/q”为假 B “ ”为真 Cp 真 q 假 Dp 假 q 真不等式 的解集是 ( A 02|2x)A B C D|2|1|x1|等比数列a n中, ( C 821913则, 若, )A27 B 27 C D327376给出下面类比推理命题(其中 Q 为有理数集,R 为实数集,C 为复数集):“若 ”类比推出0, 则、“ ”则、“若 ”类比推出,, 则 复 数、2“ ”,2, 则、“若 ”类比推出“若 ”R0, 则、 “若 ”类比推出“若 ”1|则 1|则其中类比结论正确的个数有 A1 B2 C3 D4 ( B )7在 R 上定义运算: 任意实数 x 恒成立,)(y 1)( C )A B 02) |3|x 3 分|)由 2 得 ,32x 0)8(0643,2 即 ,即 的取值范围是 6 分8,(3,2()令 9 分222 )(4)(则6当 上单调递增,),4(30,42 在, 即 函 数 数 上也单调递增 11 分),623在当 x=6 时, 取得最小值即 得最小值 27(平方米)N|=6 米,| 13 分答:当 N 的长度分别是 ,6 米时,矩形 面积最小,最小面积是27 平方米. 14 分19 (本小题满分 14 分)已知函数 ).0()若 上单调递增,求 a 的取值范围;),1(在)由 2 分22)(得欲使函数为 上单调增函数,则 上恒成立,), ,10在即不等式 上恒成立,也即 上恒成立 4 分),102在,12在上述问题等价于 ,2)(x而 上的减函数,则 ),为 在 0)(a, 于 是()若定义在区间 D 上的函数 对于区间 D 上的任意两个值 x1、x 2 总有以下不等式(立,则称函数 为区间 D 上的“凹函数”()(2112)(函数” ,并对你的判断加以证明07证明:由 得 )1(21)( 211 7 分 8 分212121l 10 分212121 )()(4)( 又 1 分212121212121 44)()( x, 13 分, 、得 21212122121 l)( 即 ,从而由凹函数的定义可知函数为凹函数 14 分)(2)(1120 (本小题满分 14 分)已知数列 .*,141:且满 足(1)计算 x2,x 3,x 4 的值;(2)试比较 2 的大小关系;(3)设 ,S n 为数列a n前 n 项和,求证:当 .|a 时 ,解:(1) 3 ;5432(2)当 121 又 0,3411 2211 则相 反 , 而与8以此类推有: 8 分2,12)当 时, 1,1341 则 |2|2|2|1 )( )1)(1 14 分 11 12 2)()(
若已知一个栈的进栈序列是1,2,3…n,其输出序列是P1,P2,P3,…PN,若P1=n,则Pi(1 A.I B.n-i C.n-i+1 D.不确定
若已知一个栈的输入序列为1,2, 3,…,n;其输出序列为P1,P2,…,Pn。若P1=n,则Pi为( )。A.i B.n-iC.n-i+ 1 D.不确定
栈是一种先进后出的线性表,输入序列为1,2,3.。。。n,输出序列为P1,P2,P3,……,若P1=n,即P2=n-1,……;和P的序号的关系为:P的序号与输出的数的和为n+1,所以pi的序号为,n+1-i;
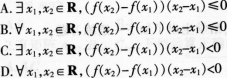

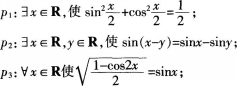
p4:若sinx=cosy。则x+y=π/2。其中假命题个数为( )。
B、1
C、2
D、3
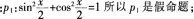

数据结构里,若已知一个栈的入栈序列是1,2,3,…,n,其输出序列为p1,p2,p3,…,pn,若p1=n,则pi为()。
- A、n-i+1
- B、i
- C、n-i
- D、不确定
正确答案:A
更多 “广东省华南师大附中2007—2008学年度高三综合测试(三)数学试题(理科)” 相关考题
相关内容
最新试卷
热门试卷
- 西安交通大学22春《电路》在线作业三及答案参考58-
- 重庆大学2021年12月《商务沟通》期末考核试题库及答案参考55-
- 西安交通大学22春《电算化会计》在线作业一及答案参考17-
- 重庆大学2021年12月《商务沟通》期末考核试题库及答案参考4-
- 西安交通大学22春《生药学》在线作业一及答案参考88-
- 西安交通大学2021年12月《程序设计基础》期末考核试题库及答案参考91-
- 西安交通大学22春《生药学》在线作业二及答案参考11-
- 西安交通大学2021年12月《程序设计基础》期末考核试题库及答案参考24-
- 西安交通大学2021年12月《病理学》期末考核试题库及答案参考80-
- 西安交通大学2021年12月《多媒体技术》期末考核试题库及答案参考16-
