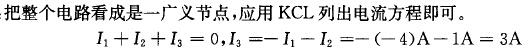资产评估学教程(第三版)复习题部分习题答案
△ABC中,AB=3,BC=4,则AC边的长满足( )。
A.AC=5
B.AC>1
C.AC<7
D.1<AC<7
三角形的任意两边之和大于第三边,任意两边之差小于第三边,BC-AB=1,BC+AB=7,所以1<AC<7。
A.5A±3A
B.5A±2A
C.6±2A
D.5A±1A

血清中的C1作用对象是( )
A.C2aC3a
B.C3aC5a
C.C3bC4b
D.C2C4
E.C5aC3b
给定关系r(R),r满足(44)函数依赖。

①A→B
②A→C
③AB→C
④C→A
⑤BC→A
⑥AC→B
A.1、2、3
B.2、3、4、5
C.3、4、5、6
D.1、2、3、6
解析:①r不满足FD:A→B。因为对于元组(3,5,6)和(3,4,6),有t1(A)=3=t2(A),但是t1B)=5[*]t2(B)=4。②表中A列不等值的所有元组满足FD:A→C,称这类元组“空满足”该FD。另外,还有两个满足条件“A列等值时C列也等值”的元组,即t1(A)=3=t2(A),而且t1(C)=6=t2(C)。于是关系r满足FD:A→C,因为其所有元组都满足该FD。③关系r满足FD:AB→C。表中没有元组在A列和B列有相同表项,所有元组都空满足该FD。因此,r满足FD:AB→C。④关系r满足FD:C→A,实际上t1(C)=6=t2(C),且t1(A)=3=t2(A)。其余元组都空满足该FD。⑤关系r满足FD:BC→A。所有元组都空满足该FD。⑥关系r不满足FD:AC→B。考虑下面两个元组t1(AC)=(3,6)=t2(AC),但t1(B)=5[*]t2(B)=4。
摘要:第一章导论3、(1)abcd(3)ab(5)abde第二章资产评估的程序与基本方法3、(1)abd(7)ac(2)abcd(3)ac(4)ab(5)abe(6)be5、[(1.5-1.2)×10000×12×(1-33%)]×[1-1/(1+10%)5]/10%=91434(元)第三章机器设备评估(9)abc(11)bc2、(1)cd(3)bc(5)abe(7)ace3、(1)1)估算重置成本重置成本=100×150%÷110%+5×150%÷125%+2×150%÷130%=144.67(万元)2)估算加权投资年限加权投资年限=10×136.36÷144.67+5×6÷144.67+2×2.3÷144.67=9.66年3)估算实体性贬值率实体性贬值率=9.66÷(9.66+6)=61.69%4)估算实体性贬值实体性贬值=重置成本×实体性贬值率=144.67×61.69%=89.25(万元)5)功能性贬值估算第一步,计算被评估装置的年超额运营成本(5-4)×12000=12000(元)第二步,计算被评估装置的年净超额运营成本12000×(1-33%)=8040(元)第三步,将被评估装置的年净超额运营成本,在其剩余使用年限内折现求和,以确定其功能性贬值额8040×(P/A,10%,6)=8040×4.3553=35016.61(元)=3.5万元6)求资产价值待评估资产的价值=重置成本-实体性贬值-功能性贬值=144.67-89.25-3.5=51.92(万元)(2)1 1)估算重置成本重置成本=100×120%÷105%+10×120%÷115%=124.
 (2) Y2=A+ABC+AB
(2) Y2=A+ABC+AB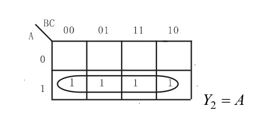 (3) Y3=AC+AB+AB
(3) Y3=AC+AB+AB (4) Y4=ABC+AC+C
(4) Y4=ABC+AC+C
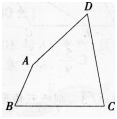
(1)若∠B与∠D互补,求AC2的值;
(2)求平面四边形ABCD面积的最大值。


B.2A
C.3A
D.4A