20202021大连市七年级数学下期末试题(带答案)

直线AB，CD相交于点O。

（1）OE，OF分别是∠AOC，∠BOD的平分线。画出这个图形。

（2）射线OE，OF在同一条直线上吗？

（3）画∠AOD的平分线OG。OE与OG有什么位置关系？

⊿ABC中，∠ABC、∠ACB的平分线相交于点O。

（1）若∠ABC = 40°，∠ACB = 50°，则∠BOC = 。

（2）若∠ABC +∠ACB =116°，则∠BOC = 。

（3）若∠A = 76°，则∠BOC = 。

（4）若∠BOC = 120°，则∠A = 。

（5）你能找出∠A与∠BOC 之间的数量关系吗？


正确答案：
（1）135°；（2）122°；（3）128°；（4）60°；（5）∠BOC = 90°+ ∠A

已知某瞬时平面图形上O点的加速度为a0。图形的角速度ω=0，角加速度为α0。则图形上过O点并垂直于a0的直线mn上各点加速度的方向应是( )。


A.指向O点
B.垂直mn直线
C.与mn直线成θ角
D.沿mn直线背离O点

答案：B
解析：
用基点法求加速度

已知某瞬时平面图形上O点的加速度为a0。图形的角速度ω=0，角加速度为α0。则图形上过O点并垂直于a0的直线mn上各点加速度的方向应是( )。


A.指向O点
B.垂直mn直线
C.与mn直线成θ角
D.沿mn直线背离O点

答案：B
解析：
用基点法求加速度

曲柄OA在如图30-9所示瞬时以ω的角速度绕轴O转动，并带动直角曲杆O1BC在如图所示平面内运动。若取套筒A为动点，杆O1BC为动系，则牵连速度大小为（　　）。


答案：B
解析：
{图}

2020-2021大连市七年级数学下期末试题(带答案)选择题如图，直线EC与MN相交于点O,AO丄EC,OE平分ZBON,若ZEON=20,则一副直角三角板如图放置，点C在FD的延长线上,AB/CF,ZF=ZACB=90,则ZA.10B.15C.18D.30。如图所示的表格是某次篮球联赛部分球队的积分表，则下列说法不正确的是()队名比赛场数胜场负场积分前进1410424光明149523远大147a21卫星14410b钢铁1401414A.负一场积1分，胜一场枳2分B.卫星队总积分以18C.远大队负场数7D.某队的胜场总积分可以等于它的负场总积分点P(m+3,m+1)在x轴上，则P点坐标为()A.(0,-2)B.(0,-4)C.(4,0)D.(2,0)已知：二;是关于x,y的二元一次方程x-ay=3的一个解，则a的值为()A.1B.-1C.2D.-2A.1B.-1C.2D.-2ax+cy=l/的解，则养b间的关系是（cx-by=zA.4b-9a=lB.3d+2b=lC.4/?一9。=一1关于x的不等式x-b0恰有两个负整数解，则b的取值范閑是A.-3b-2B.-3b-2C.-3b-2如图，将AAEC沿EC边上的中线AD平移到AEC的位置，阴影部分三角形的面积为4.若AAl,则AD等于（6.己知x=32是方程叫D.D.9a+4/?=1-3b-2已知AABC的面积为9,39.2C.3己知m=百十则以下对m的估算正确的（）3D-2A.10.在平面直角坐标系中，点3在第四象限，它到X轴和）轴的距离分别是2、5,则点B的坐标为（）2m3B.3m4C.4m5D.5m6C.125D.135B.(2-5)A.(5-2)C（5,2）D（2、5）11.如图，AB/CD,DE丄BE,BF、DF分别为ZABE、ZCDE的角平分线，则ZBFD=j45x=y-3560(x-2)+35=y45x=y+35y-60(x-2)=3512某中学计划租用若干辆汽车运送七年级学生外出进行社会实践活动，如果一辆车乘坐45人，那么有35名学生没有车坐；如果一辆车乘坐60人，那么有一辆车只坐了35人，并且还空出一辆车设计划租用X辆车，共有y名学生则根据题意列方程组为（）45x-35=y-60(x-2)=y-35J45x+35=y60(.r-1)+35=y二、填空题13.若a，=64,则扬=14如图，边长为10cm的正方形ABCD先向上平移4cm,再向右平移2cm,得到正方形ABCD,则阴影部分面积为ADTOC o 1-5 h z15已知二元一次方程2x3尸6,用关于x的代数式表示y,则尸.16.若将点A（1,3）向左平移2个单位，再向下平移4个单位得到点则点B的坐标为x+y=3（x=a17若二元一次方程组锂3(x-l)解不等式组13，并求出它的所有整数解的和.X0:.xb综合上述可得-3/?=2或A，D=-j（舍），故选A.点睛：本题主要平移的性质，解题的关键是熟练掌握平移变换的性质与三角形中线的性质、相似三角形的判定与性质等知识点.B解析：B【解析】【分析】直接化简二次根式，得出荷的取值范围，进而得出答案.【详解】*/m=5/44-5/3=2+羽,132,/3ma=8.:.需=2故答案为2【点睛】本题考查平方根、立方根的定义，解题关键是一个正数的平方根有两个，他们互为相反数.14.【解析】【分析】如图交于其延长线交于利用平移的性质得到再利用四边形为矩形得到然后计算出和即可得到阴影部分面积【详解】解：如图交于其延长线交于边长为的正方形先向上平移再向右平移得到正方形易得四边形为矩33解析：48c/?2【解析】【分析】如图，AE交AD于尸，其延长线交BC于E，利用平移的性质得到A8/AB,BCHBC,FE=4,AF=2,再利用四边形ABEF为矩形得到EF=初=10,然后计算出阳和DF即可得到阴影部分面积.【详解】解：如图，交AD于F,其延长线交BC于E,边长为10期的正方形ABCD先向上平移4（加再向右平移2伽，得到正方形ABCD,.AR/AB,BCHEC,BE=4,4F=2，易得四边形ABEF为矩形，:.EF=AB=10,:FE=6,DF=8,阴影部分面积=6x8=48(cm2).故答案为：48c7【点睛】本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和人小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点.连接各组对应点的线段平行且相等.15.【解析】【分析】把x看做己知数求出y即可【详解】解：方程2x-3y二6解得：y二故答案为【点睛】此题考查了解二元一次方程解题的关键是将x看做已知数求出y解析:2x63【解析】【分析】把X看做已知数求出y即可.【详解】解：方程2x-3y=6,解得:2x-6y=2x-6故答案为3【点睛】此题考查了解二元一次方程，解题的关键是将x看做已知数求出y.16.(-1-1)【解析】试题解析:点B的横坐标为1-2纵坐标为3-4=1所以点B的坐标是(-1-1)【点睛】本题考查点的平移规律；用到的知识点为：点的平移左右平移只改变点的横坐标左减右加；上下平解析：(-1,-1)【解析】试题解析：点B的横坐标为1-2=-1,纵坐标为3-4=-1,所以点B的坐标是(-1,-1).【点睛】本题考查点的平移规律；用到的知识点为：点的平移，左右平移只改变点的横坐标，左减右加；上下平移只改变点的纵坐标，上加下减.17.【解析】【分析】把xy的值代入方程组再将两式相加即可求出a-b的值【详解】将代入方程组得：+得：4a-47则a-故答案为【点睛】本题考查二元一次方程组的解解题的关键是观察两方程的系数从而7解析：-4【解析】【分析】把x、y的值代入方程组，再将两式相加即可求出a-

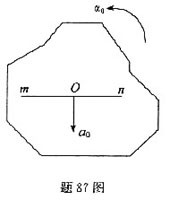
已知某瞬时平面图形上O点的加速度为a0。图形的角速度ω=0，角加速度为α0。则图形上过O点并垂直于a0的直线mn上各点加速度的方向应是( )。


A.指向O点
B.垂直mn直线
C.与mn直线成θ角
D.沿mn直线背离O点

答案：B
解析：
用基点法求加速度

如图，已知圆C与x轴相切于点T(1，0)，与y轴正半轴交于两点A，B(B在A的上方)且AB=2，则圆C在点8处的切线在x轴上的截距_________。


答案：
解析：

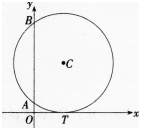
解析：连接BC，CT，设半径为r，由于T为切点，所以CT⊥x轴，点C到AB的距离为1，

如图，边长为a的正方形ABCD中，点E是对角线BD上的一点，且BE=BC，点P在EC上，PM⊥BD于M，PN⊥BC于N，则PM+PN=________。


答案：
解析：

解析：作EK⊥BC于K，连接BP，由△EBC的面积等于△PBE和△PBC的面积之和且BE=

如图所示。直线AB与DF相交于点0，OD平分∠BOC，EO⊥D0，垂足为0，则∠COF与∠BOE的差为()。

A.30o
B.45o
C.60o
D.90o

答案：D
解析：
∠COF+∠COD=180°，∠BOE+∠BOD=90°，且∠COD=∠BOD，两式相减可知∠COF- ∠BOE=90°。

如图，AB是⊙O的直径，AC是弦，直线EF和⊙O相切与点C，AD⊥EF，垂足为D。
(1)若 ∠DAC=63°，求∠BAC；(5分)
(2)若把直线EF向上平行移动，如图，直线EF交 ⊙O于G和C两点，若题中的其他条件不变，这时与∠DAC相等的角是哪一个 为什么 (5分)



答案：
解析：
(1)证明：连接OC，则OC⊥EF，且OC=OA，易得∠OCA=∠OAC。 ∵AD⊥EF，∴OC∥AD。∴∠OCA=∠CAD，∴∠CAD=∠OAC=63°
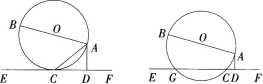
(2)与∠CAD相等的角是∠BAG。
证明如下：如图，连接BG。∵四边形ACGB是⊙O的内接四边形．
∴∠ABG+∠ACG=180°。
∵D，C，G共线,∴∠ACD+∠ACG=180°。
∴∠ACD=∠ABG。
∵AB是⊙O的直径,∴∠BAG+∠ABG=90°
∵AD⊥EF∴∠CAD+∠ACD=90°∴∠CAD=∠BAG

更多 “20202021大连市七年级数学下期末试题(带答案)” 相关考题
考题 分别用分析法，综合法证明如下命题。 命题：如图。三角形ABC的角B和角C的角平分线相交于点O，过点O作平行于底边BC的直线，交AB边于点D，交AC边于点E，则DE=BD+EC。 答案：解析：
查看答案
考题 如图，在A、B两点，放置两个点电荷，它们的带电量分别为q---1,q---2，MN是过A、B的直线，P是直线上的一点，若P点的场强为0，则（　　）。 答案：B解析：电场强度是矢量，当空间的电场是由几个点电荷共同激发的时候，空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和。若两个点电荷电性相同，则P点的电场一定
查看答案
考题 已知某瞬时平面图形上O点的加速度为a0。图形的角速度ω=0，角加速度为α0。则图形上过O点并垂直于a0的直线mn上各点加速度的方向应是( )。A.指向O点 B.垂直mn直线 C.与mn直线成θ角 D.沿mn直线背离O点答案：B解析：用基点法求加速度
查看答案
考题 如图所示，直角刚杆AO=2m，BO=3m，已知某瞬时A点的速度vA= 6m/s，而B点的加速度与BO成β=60°角。则该瞬时刚杆的角加速度α的大小为：答案：D解析：提示：由 vA=OA * ω，则B点法向加速度an=OB*ω2，所以 acosβ=an，aτ=OB *α=asinβ。
查看答案
考题 如图所示，直角刚杆AO=2m，BO=3m，已知某瞬时A点的速度vA= 6m/s，而B点的加速度与BO成β=60°角。则该瞬时刚杆的角加速度α的大小为：答案：D解析：提示：由 vA=OA * ω，则B点法向加速度an=OB*ω2，所以 acosβ=an，aτ=OB *α=asinβ。
查看答案
考题 如图3，△ABC向右平移后得到△DEF，且点B、C、E、F在同一直线上，已知BF=8，CE=2，则平移的距离是__________。答案：解析：5
查看答案
考题 曲柄OA在如图30-9所示瞬时以ω的角速度绕轴O转动，并带动直角曲杆O1BC在如图所示平面内运动。若取套筒A为动点，杆O1BC为动系，则牵连速度大小为（　　）。 答案：B解析：{图}
查看答案
考题 如图：已知直线PA：y=kx+4与直线PB：y=x+b相交于P（1，2），且分别与x轴、y轴交于点A、B。则四边形OAPB的面积是（）。 A. 3/2 B. 2 C. 5/2 D. 3 答案：C解析：解题指导： 四边形OAPB的面积是两个三角形面积的差。直线PA与x轴交于A点（2，0），可知，OA=2，P点（1，2）可知PA=2，PB=1，直线PB与y轴交于B点（0，1），可知直线PB与x轴交于Q点（-1，0），即PQ=1，则大三角形ΔPAQ底边AQ长为2+1=3，面积为3×2÷2=3，直角三角形ΔBOQ的面积=OB×OQ÷2=1×1÷2=0.5，则四边形OAPB的面积=3-0.5=2.5，故答案为C。
查看答案
考题 曲柄OA在如图30-9所示瞬时以ω的角速度绕轴O转动，并带动直角曲杆O1BC在如图所示平面内运动。若取套筒A为动点，杆O1BC为动系，则牵连速度大小为（　　）。 答案：B解析：{图}
查看答案
考题 如图所示，真空中有A、B两个等量异种点电荷，0、M、N是AB连线的垂线上的三个点，且A O>OB。一个带负电的检验电荷仅在电场力的作用下，从M点运动到N点，其轨迹如图中实线所示。若M、N两点的电势分别为M和N，检验电荷通过M、Ⅳ两点的动能分别为Ekm和Ekn，则( )。 答案：B解析：由于带负电的检验电荷仅在电场力的作用下由M运动到Ⅳ，说明检验电荷受到的电场力方向大致是向左的，故A带正电，B带负电，又因为AO>OB，所以M、Ⅳ两点的电势并不相等，M处于更接近B点的等势面上，N处于更远离B点的等势面上，故φM＜φN。由于检验电荷带负电，故带负电的检验电荷处于N点时的电势能小于在M点时的电势能．故在Ⅳ点时的动能大于在M点时的动能，即EKM＜EKN，B项是正确的。
查看答案
相关内容
最新试卷
热门试卷