自学考试真题:1310全国全国自考线性代数(经管类)真题


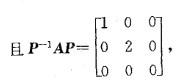
若矩阵Q=(a1,a2,a3),则Q-1AQ=


 ,则A^3的秩为________
,则A^3的秩为________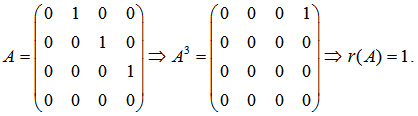
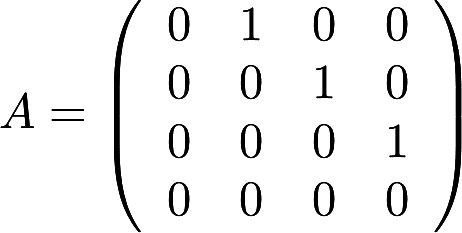 ,则A^3的秩为________
,则A^3的秩为________
全国2013年10月高等教育自学考试线性代数(经管类)试题课程代码:04184一、单项选择题(本大题共5小题,每小题1分,共5分)1设行列式=1,=-2,则=( )A-3 B-1 C1 D32设矩阵A=,则A-1=( )A B C D3设A为mn矩阵,A的秩为r,则( )Ar=m时,Ax=0必有非零解Br=n时,Ax=0必有非零解Crm时,Ax=0必有非零解Drn时,Ax=0必有非零解4设4阶矩阵A的元素均为3,则r(A)=( )A1 B2 C3 D45设1为3阶实对称矩阵A的2重特征值,则A的属于1的线性无关的特征向量个数为( )A0 B1 C2 D3二、填空题(本大题共10小题,每小题2分,共20分)6设A为2阶矩阵,将A的第1行加到第2行得到B,若B=,则A=_7设A为3阶矩阵,且|A|=2,则|2A|=_8若向量组线性无关,则数a的取值必满足_9设向量,则=_10设A=,b=,若非齐次线性方程组Ax=b有解,则增广矩阵的行列式=_11齐次线性方程组x1+x2+x3=0的基础解系中所含解向量的个数为_12设向量,则的长度=_13已知-2是矩阵A=的特征值,则数x=_14已知矩阵A=与对角矩阵D=相似,则数a=_15已知二次型正定,则实数t的取值范围是_三、计算题(本大题共7小题,每小题9分,共63分)16计算行列式D=.17已知向量且,求(1)数k的值; (2)A10.18已知矩阵A=,B=,求矩阵X,使得XA=B.19求向量组的秩和一个极大线性无关组,并将向量组中的其余向量由该极大线性无关组线性表出.20已知齐次线性方程组Ax=0的一个基础解系为,求r(A)及该齐次线性方程组.21设向量组.求一个非零向量,使得与均正交.22用配方法化二次型为标准形,并写出所用的可逆性变换.四、证明题(本题7分)23设A是mn矩阵,证明齐次线性方程组Ax=0与ATAx=0同解.
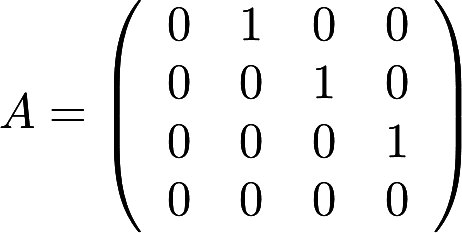 ,则A^3的秩为________
,则A^3的秩为________

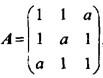 ,已知A的伴随矩阵的秩为1,则a=( )。
,已知A的伴随矩阵的秩为1,则a=( )。
A. -2 B. -1 C. 1 D. 2

 ,已知A的伴随矩阵的秩为1,则a=( )。
,已知A的伴随矩阵的秩为1,则a=( )。
A. -2 B. -1 C. 1 D. 2

 ,已知A的伴随矩阵的秩为1,则a=( )。
,已知A的伴随矩阵的秩为1,则a=( )。
A. -2 B. -1 C. 1 D. 2

