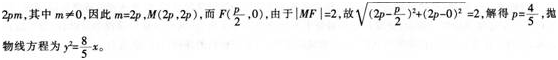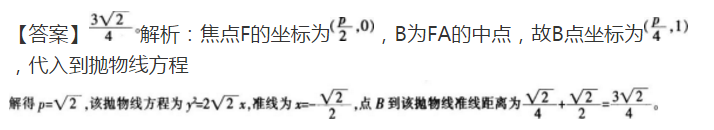高考数学抛物线试题汇编
已知过点(0,4),斜率为-1的直线l与抛物线C:y2—2px(b>;0)交于A,B两点.
(I)求C的顶点到2的距离;
(Ⅱ)若线段AB中点的横坐标为6,求C的焦点坐标.
抛物线y2=-4x的准线方程为 ( )
A.x=-1
B.x=1
C.y=1
D.Y=-l
本题主要考查的知识点为抛物线.【应试指导】
抛物线y2=3x的准线方程为 ( )

A.A
B.B
C.C
D.D
本题主要考查的知识点为抛物线的准线.【应试指导】
(A) x2 + y2 + (1-x)2 = 9
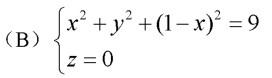
(C) (1-z)2 + y2 + z2 = 9
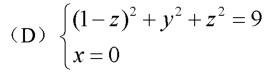


第三节抛物线高考试题考点一 抛物线的定义和标准方程1.(2010年陕西卷,理8)已知抛物线y2=2px(p0)的准线与圆x2+y2-6x-7=0相切,则p的值为()(A)(B)1 (C)2(D)4解析:圆x2+y2-6x-7=0化为标准方程为(x-3)2+y2=16,圆心为(3,0),半径是4,抛物线y2=2px(p0)的准线是x=-,3+=4,又p0,解得p=2.故选C.答案:C2.(2011年辽宁卷,理3)已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为()(A) (B)1 (C) (D)解析:|AF|+|BF|=xA+xB+=3,xA+xB=.线段AB的中点到y轴的距离为=.故选C.故选C.答案:C3.(2012年四川卷,理8)已知抛物线关于x轴对称,它的顶点在坐标原点O,并且经过点M(2,y0).若点M到该抛物线焦点的距离为3,则|OM|等于()(A)2 (B)2(C)4 (D)2解析:由题意设抛物线方程为y2=2px(p0),则M到焦点的距离为xM+=2+=3,p=2,y2=4x.=42,|OM|=2.故选B.答案:B4.(2010年上海卷,理3)动点P到点F(2,0)的距离与它到直线x+2=0的距离相等,则点P的轨迹方程是.解析:由抛物线的定义知,点P的轨迹是以F为焦点,定直线x+2=0为准线的抛物线,故其标准方程为y2=8x.答案:y2=8x5.(2012年陕西卷,理13)如图所示是抛物线形拱桥,当水面在l时,拱顶离水面2 m,水面宽4 m.水位下降1 m后,水面宽m.解析:建立如图所示的平面直角坐标系,设抛物线方程为x2=-2py(p0),则A(2,-2),将其坐标代入x2=-2py,得p=1.x2=-2y.当水面下降1 m,得D(x0,-3)(x00),将其坐标代入x2=-2y得=6,x0=,水面宽|CD|=2 m.答案:26.(2010年浙江卷,理13)设抛物线y2=2px(p0)的焦点为F,点A(0,2),若线段FA的中点B在抛物线上,则B到抛物线准线的距离为.解析:由已知得B点的纵坐标为1,横坐标为,即B,将其代入y2=2px得1=2p,解得p=,则B点到准线的距离为+=p=.答案:考点二 抛物线的几何性质及其应用1.(2011年四川卷,理10)在抛物线y=x2+ax-5(a0)上取横坐标为x1=-4,x2=2的两点,过这两点引一条割线,有平行于该割线的一条直线同时与抛物线和圆5x2+5y2=36相切,则抛物线顶点的坐标为()(A)(-2,-9)(B)(0,-5)(C)(2,-9) (D)(1,-6)解析:当x1=-4时,y1=11-4a;当x2=2时,y2=2a-1,所以割线的斜率k=a-2.设直线与抛物线的切点横坐标为x0,由y=2x+a得切线斜率为2x0+a,2x0+a=a-2,x0=-1.直线与抛物线的切点坐标为(-1,-a-4),切线方程为y+a+4=(a-2)(x+1),即(a-2)x-y-6=0.圆5x2+5y2=36的圆心到切线的距离d=.由题意得=,即(a-2)2+1=5.又a0,a=4,此时y=x2+4x-5=(x+2)2-9,顶点坐标为(-2,-9).故选A.答案:A2.(2009年四川卷,理9)已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是()(A)2 (B)3(C)(D)解析:如图所示,动点P到l2:x=-1的距离可转化为点P到点F的距离.由图可知,距离和的最小值即F到直线l1的距离d=2.故选A.答案:A3.(2009年福建卷,理13)过抛物线y2=2px(p0)的焦点F作倾斜角为45的直线交抛物线于A、B两点,若线段AB的长为8,则p=.解析:F,设AB:y=x-,与y2=2px联立,得x2-3px+=0.xA+xB=3p.|AB|=xA+xB+p=4p=8,得p=2.答案:24.(2010年大纲全国卷,理15)已知抛物线C:y2=2px(p0)的准线为l,过M(1,0)且斜率为的直线与l相交于点A,与C的一个交点为B,若=,则p=.解析:如图所示,由AB的斜率为,知=60,又=,M为AB的中点.过点B作BP垂直准线l于点P,则ABP=60,BAP=30.|BP|=|AB|=|BM|,M为焦点,即=1,p=2.答案:2考点三 直线与抛物线位置关系1.(2013年大纲全国卷,理11)已知抛物线C:y2=8x与点M(-2,2),过C的焦点且斜率为k的直线与C交于A、B两点,若=0,则k等于()(A)(B) (C) (D)2解析:法一设直线方程为y=k(x-2),A(x1,y1)、B(x2,y2),由得k2x2-4(k2+2)x+4k2=0,x1+x2=,x1x2=4,由=0,得(x1+2,y1-2)(x2+2,y2-2)=(x1+2)(x2+2)+k(x1-2)-2k(x2-2)-2=0,代入整理得k2-4k+4=0,解得k=2.故选D.法二如图所示,设F为焦点,取AB中点P,过A、B分别作准线的垂线,垂足分别为G、H,连接MF,MP,由=0,知MAMB,则|MP|=|AB|=(|AG|+|BH|),所以MP为直角梯形BHGA的中位线,所以MPAGBH,所以GAM=AMP=MAP,又|AG|=|AF|,|AM|=|AM|,所以AMGAMF,所以AFM=AGM=90,则MFAB,所以k=-=2.答案:D2.(2010年辽宁卷,理7)设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PAl,A为垂足,如果直线AF的斜率为-,那么|PF|等于()(A)4(B)8 (C)8(D)16解析:如图所示,直线AF的方程为y=-(x-2),与准线方程x=-2联立得A(-2,4).设P(x0,4),代入抛物线y2=8x,得8x0=48,x0=6,|PF|=x0+2=8,选B.答案:B3.(2012年安徽卷,理9)过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点,O为坐标原点.若|AF|=3,则AOB的面积为()(A)(B)(C)(D)2解析:如图所示,由题意知,抛物线的焦点F的坐标为(1,0),又|AF|=3,由抛物线定义知:点A到准线x=-1的距离为3,点A的横坐标为2.将x=2代入y2=4x得y2=8,由图知点A的纵坐标y=2,A(2,2),直线AF的方程为y=2(x-1).联立直线与抛物线的方程解之得或由图知B,SAOB=|OF|yA-yB|=1|2+|=.故选C.答案:C4.(2009年天津卷,理9)设抛物线y2=2x的焦点为F,过点M(,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于点C,|BF|=2,则BCF与ACF的面积之比等于()(A)(B)(C)(D)解析:如图所示,设过点M(,0)的直线方程为y=k(x-),代入y2=2x并整理,得k2x2-(2k2+2)x+3k2=0,设A(x1,y1),B(x2,y2),则x1+x2=,x1x2=3,因为|BF|=2,所以|BB|=2,x2=2-=,从而x1=2.设点F到直线AC的距离为d,则=.故选A.答案:A5.(2009年大纲全国卷,理9)已知直线y=k(x+2)(k0)与抛物线C:y2=8x相交于A、B两点,F为C的焦点,若|FA|=2|FB|,则k等于()(A)(B) (C)(D)解析:将y=k(x+2)代入y2=8x,得k2x2+(4k2-8)x+4k2=0.设交点的横坐标分别为xA,xB,则xA+xB=-4,xAxB=4.又|FA|=xA+2,|FB|=xB+2,|FA|=2|FB|,2xB+4=xA+2.xA=2xB+2.将代入得xB=-2,xA=-4+2=-2.故xAxB=4.解之得k2=.而k0,k=,满足0.故选D.答案:D6.(2013年安徽卷,理13)已知直线y=a交抛物线y=x2于A,B两点.若该抛物线上存在点C,使得ACB为直角,则a的取值范围为.解析:设直线y=a与y轴交于点M,抛物线y=x2上要存在C点,使得ACB为直角,只要以|AB|为直径的圆与抛物线y=x2有交点即可,也就是使|AM|MO|,即a(a0),所以a1.答案:1,+)7.(2012年重庆卷,理14)过抛物线y2=2x的焦点F作直线交抛物线于A,B两点,若|AB|=,|AF|BF|,则|AF|=.解析:由于y2=2x的焦点坐标为,设AB所在直线的方程为y=k,A(x1,y1),B(x2,y2),x10)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F
B.(x+2)2+y2=4
C.(x-2)2+y2=16
D.(x-2)2+y2=4
B.(x+2)2+y2=4
C.(x-2)2+y2=16
D.(x-2)2+y2=4
(1)求抛物线的方程式;