附录A习题参考答案
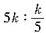
B.
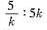
C.
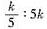
D.
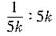
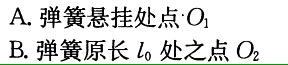

答案:C


答案:D

现代控制理论及其MATLAB 实现- 1 - 附录 A 习题参考答案A1 第 1 章习题参考答案1-1 解:串联弹簧等效刚度系数为212121111kkkkkkK以系统静平衡位置为坐标y 和 z 的原点)t(pKz)yz(fzM(E1)yk)yz(f3(E2)令zx1(E3)zx2(E4)yx3( E5)由式( E3)和( E4)可得21xzx( E6)由式( E2)、( E4)和( E5)可得3323xfkxyx(E7)由式( E4)、( E1)和( E7)可得)t(pMzMK)yz(Mfzx12)t (pMxMKxMk1133(E8)于是,系统状态空间模型的向量表达式为附录 A 习题参考答案- 2 - )t(pMxxxfkMkMKxxx01010001032133321x3213100 xxxxy3211001xxxxz1-2 解:由基尔霍夫定理得iuvdtdiLRi111(回路电压)(E1)dtdvcdtdvcii112221(节点电流)( E2)dtducdtdvcio3222(节点电流)(E3)12vuvo(回路电压)(E4)22vdtdiL(回路电压)(E5)设12214321vviixxxxx由式( E1)可得iiuLxLxLRuLvLiLRdtdix1111411111(E6)由式( E5)可得322211xLvLdtdix(E7)由式( E2)(E4)可得现代控制理论及其MATLAB 实现- 3 - 2323121311323121323iccccccccicccccccdtdvx23231213113231213xccccccccxccccccc(E8)2323121313231213214iccccccciccccccccdtdvx23231213132312132xcccccccxcccccccc(E9)系统状态方程的向量表达式为iuLccccccccccccccccccccccccccccccLLLR000100000100100323121332312131323121313231213xx由式( E4)直接可得输出方程,即x11004321xxvvuo1-3 解:(1)能观测规范型u1027110351100001000010 xxx0001y能观测规范型u1365610100301050011000 xxx1000y附录 A 习题参考答案- 4 - (2)能观测规范型u1520523100010 xxuy2001x能观测规范型u025510201300 xxuy2100 x(3)仿照线性定常系统能观测规范型状态空间模型的建立方法,如下选取状态变量:yx1(E1)uxx012(E2)uxx123(E3)式中,0和1为待定时变系数。uxx021(E4)uxx132(E5)为求3x的一阶导数,从式(E1)开始,依次向下进行迭代,可得uyuxx0012(E6)uuuyuxx100123( E7)对上式求一阶导数,可得uuuuuyx)(11000332(E8)由给定微分方程可得uuuyeyytyt)(852333(E9)从式( E6)和( E7)求出y和y且将其与式(E9)一并代入式(E8) ,经化简可得uuuxe)ux()uuux( txt8523130210033现代控制理论及其MATLAB 实现- 5 - uuuuu110002u)t(u)(txxxet1000321328532u)tt(1001031为使状态方程不含输入量的导数项,令50tt5828001再引入系数985312100102tttt可得utxxxext23213332(E10)系统状态方程的向量表达式为u)t()t(bxAx式中:te)t(t321000103A9855852210ttt)t(b输出方程为Cxy1x其中,001C(4)设yx1yx2yx3可得21xx附录 A 习题参考答案- 6 - 32xxuxxxxxxyuyyyyyyx)(12121312338438431xy1-4 解: (1)2754361015045152342ssssss)s(u)s(Y)s(W(a)能控规范型及约当规范型能控规范型u100010365427100001000010 xxx01545150y约当规范型u9127102713000130001300001zzz291576567521215y(b)能控规范型及约当规范型能控规范型u000110100360105400127000 xxx360105150y现代控制理论及其MATLAB 实现- 7 - 约当规范型u10013000130001300001zzz2456075245y(2)549957132016234234ssssssss)s(u)s(Y)s(W(a)能控规范型及约当规范型能控规范型u100013579954100001000010 xxx111620y约当规范型u181541541913000130000100006zzz901505486564y(b)能控规范型及约当规范型能控规范型u000113100570109900154000 xx附录 A 习题参考答案- 8 - x47483121y约当规范型u10113000130000100006zzz920325594564y1-5 解:(1)由图 1.14 可得)s(U)s(X(ssss)s(Y212345231)s(U)s(X)ssss)(s(Y212345232134523uxyyyyy)()(令yx2,yx3,yx4,)(yx35可得32xyx43xyx534xyx)(21345523uxyyyyyx)()(212345523uxxxxx)s(Y)sss()s(Us)s(X135221231123451113522xxxxuxx现代控制理论及其MATLAB 实现- 9 - 系统状态空间模型的向量表达式为21543215432110000000013125110000010000010025312uuxxxxxxxxxxxx000102xy(2)由结构图 1.15 可得)s(Ua)s(X)s(Xss)s(Y221211)s(Ua)s(X)s(Xss)s(Y22121uaxxyyy221令yx4,yx3可得34xyxuaxxxxuaxxyyyx221432213)s(Nas)s(X321nxax232)s(X)s(Uas)s(X41114111xuxaxnuaaa000100101001111000100231xx附录 A 习题参考答案- 10 - x10004xy(3)(s)N(s)ss222rs1Y(s)-+-YUs122s+继电器特性EX21XX图 A1.1 等效结构图将系统结构图1.16 等效变换为图A1.1 并如图所示在积分环节和一次项倒数环节输出端定义一个状态变量,可得)s(X)s(Y2)(1)(1sXssX)(2)(122sXssX对以上两式去分母后进行拉氏逆变换,可得xx121222xxx写成向量形式,得020021221xxxxx输出方程为2xy根据图 1.16(a),继电器特性元件的输入为e、输出为x。根据图1.16(b),x的表达式为)e()maea()ae(b)e()aema()ae(b)e()maea()e()aema()maema(x00000其中,2xue。现代控制理论及其MATLAB 实现- 11 - 1-6 解:(1)能观测规范型)k(u)k()k(1482861134241000101xx)k(u)k()k(yx001能观测规范型)k(u)k()k(638441110340124001xx)k(u)k()k(yx100(2)能观测规范型)k(u.)k()k(102141501578160961000010000101xx)k()k(yx0001能观测规范型)k(u.)k()k(505840501510078010160001960001xx)k()k(yx10001-7 解:54995713200240901023423zzzzzzz)z(u)z(Y)z(W能控规范型附录 A 习题参考答案- 12 - )k(u)k()k(1000135799541000010000101xx)k()k(yx1090240200能控规范型)k(u)k()k(0001131005701099001540001xx)k()k(yx9801904010A2 第 2 章习题参考答案2-1 解:按照矩阵指数函数条件A)t ()t (,容易验证:tttteetee)t(300000是300010011A的矩阵指数函数。ttttttttttteeeeeetetetetee)t(33300是322001012A的矩阵指数函数。2-2 解:(1)tsintcostcostsin)t(00001不满足状态转移矩阵的初值条件,故不是状态转移矩阵。(2)因I)(0,故tttttttteeeeeeee)t (22222222有可能是状态转移矩阵。现代控制理论及其MATLAB 实现- 13 - tttttttteeeeeeeedt)t (d2222424222令31200)(A因A满足A)t ()t (,故tttttttteeeeeeee)t(22222222是3120A的状态转移矩阵。(3)I)t , t(,故00000ttett)t , t(有可能是状态转移矩阵。令100100t)t , t ()t (ttA因)t(A满足)t , t ()t ()t , t (00A,故00000ttett)t , t(是1001t)t (A的状态转移矩阵。2-3 解:(1)T)(510 xtttttttteeeeeeee)t (5555555541ee)t(eteee)t (tttttt533513124852258138541xee)t(eteee)t()t(tttttt533513124852258138541xy附录 A 习题参考答案- 14 - (2)T)(225xe)ee(e)t(e)ee()ee(ete)ee(e)t (tttttt525103510251053105202253120455812445812555481xe)ee(e)t(e)ee()ee(ete)ee(e)t ()t (tttttt525103510251053105202253120455812445812555481xy2-4 解:tttteetee)t(3444000003132351152413531315291613731716915292704103232424)tsin()tcos(ee)tsin()tcos(ee)tsin()tcos(ee)t()t(ttttttx48193254337384511525292704103234)tcos()tsin、(eee)t()t (ttty2-5 解:系统矩阵1001t)t(A,显然)t()()()t (AAAA,因此状态转移矩阵为.)d)(!)d)(!d)(Ie)t , t(ttttttdt)(tt32000003121AAAA.)tt()tt(ln!)tt ()tt(ln!ttttln30302020000031002100I现代控制理论及其MATLAB 实现- 15 - 00000000ttttttlnettee受控运动分量为11122211002ttttuetlntdetd)(u), t (bx自由运动分量为105211tet)(), t (xxx系统状态方程的解为107212tue)tln( t)t (xxxx系统的输出响应为)tln( t)t()t (1201xy2-6 解:因系统矩阵ttee222102A,)t()()()t(AAAA,故状态转移矩阵为)t , t()t , t()t , t (dd)()(d)()t , t(tt022021011122100110001AAAI1481212222022001100ee)tt ()ee()tt()t , t(tttt)eett
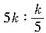
B.
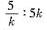
C.
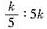
D.
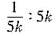
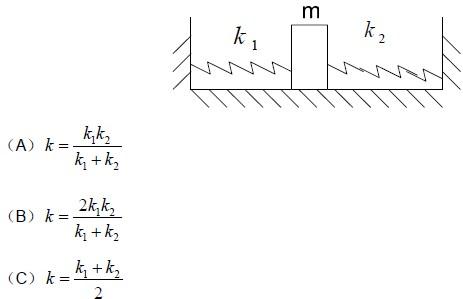
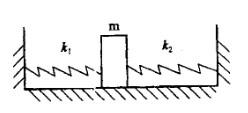
(D) k = k1+k2
此为概念题。

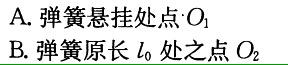

答案:C

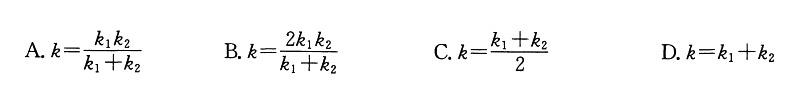
答案:D
