多元统计分析期末试题及答案
设X1,X2,…,Xn是一个样本,样本的观测值分别为x1,x2,…,xn,则样本方差s2的计算公式正确的有( )。

解析:
设X~N(μ,σ2),均值μ已知,而方差σ2未知,X1,X2,X3为总体X的样本,下列各式是统计量的有( )。
A.X1+3X2+σ2
B.X1+2μ
C.max(X1,X2,X3)
D.(X2-μ)2/σ
E.
解析:统计量是不含未知参数的样本函数。
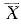 ,s2分别是样本均值和样本方差,E(X)=μ,D(X)=σ2,则有( )。
,s2分别是样本均值和样本方差,E(X)=μ,D(X)=σ2,则有( )。
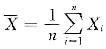 ,经计算
,经计算 从而(B)正确而(A)不正确,而(C)、(D)需要总体X服从正态分布N(μ,σ2)才能成立
从而(B)正确而(A)不正确,而(C)、(D)需要总体X服从正态分布N(μ,σ2)才能成立
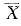 ,s2分别是样本均值和样本方差,E(X)=μ,D(X)=σ2,则有( )。
,s2分别是样本均值和样本方差,E(X)=μ,D(X)=σ2,则有( )。
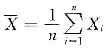 ,经计算
,经计算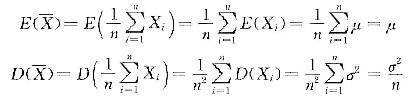 从而(B)正确而(A)不正确,而(C)、(D)需要总体X服从正态分布N(μ,σ2)才能成立
从而(B)正确而(A)不正确,而(C)、(D)需要总体X服从正态分布N(μ,σ2)才能成立
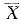 ,s2分别是样本均值和样本方差,E(X)=μ,D(X)=σ2,则有( )。
,s2分别是样本均值和样本方差,E(X)=μ,D(X)=σ2,则有( )。
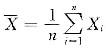 ,经计算
,经计算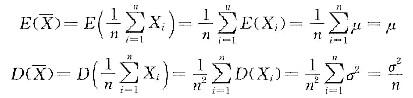 从而(B)正确而(A)不正确,而(C)、(D)需要总体X服从正态分布N(μ,σ2)才能成立
从而(B)正确而(A)不正确,而(C)、(D)需要总体X服从正态分布N(μ,σ2)才能成立摘要:4、设X=x1x2x的相关系数矩阵通过因子分析分解为3,X1的共性方差h12__________,X1的方差11__________,________________。(1)试从Σ出发求X的第一总体主成分;(2)试问当取多大时才能使第一主成分的贡献率达95%以上。1、0��1�2�2、W3(10,∑)3、R�3�1���4231161�4��1�6��1���4、0.87211.7435、T2(15,p)或(15p/(16-p))F(p,n-p) 一、填空题:1、多元统计分析是运用数理统计方法来研究解决多指标问题的理论和方法.2、回归参数显着性检验是检验解释变量对被解释变量的影响是否着.3、聚类分析就是分析如何对样品(或变量)进行量化分类的问题。通常聚类分析分为Q型聚类和R型聚类。4、相应分析的主要目的是寻求列联表行因素A和列因素B的基本分析特征和它们的最优联立表示。5、因子分析把每个原始变量分解为两部分因素:一部分为公共因子,另一部分为特殊因子。6、若x():NP(,�),=1,2,3….n且相互独立,则样本均值向量x服从的分布为_x~N(μ,Σ/n)_。二、简答1、简述典型变量与典型相关系数的概念,并说明典型相关分析的基本思想。在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数。选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对,如此下去直到两组之间的相关性被提取完毕为止。被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。2、简述相应分析的基本思想。相应分
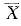 ,s2分别是样本均值和样本方差,E(X)=μ,D(X)=σ2,则有( )。
,s2分别是样本均值和样本方差,E(X)=μ,D(X)=σ2,则有( )。
 ,经计算
,经计算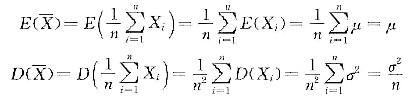 从而(B)正确而(A)不正确,而(C)、(D)需要总体X服从正态分布N(μ,σ2)才能成立
从而(B)正确而(A)不正确,而(C)、(D)需要总体X服从正态分布N(μ,σ2)才能成立
C. max(X1, X2, X3) D. (X2-μ)2/σ


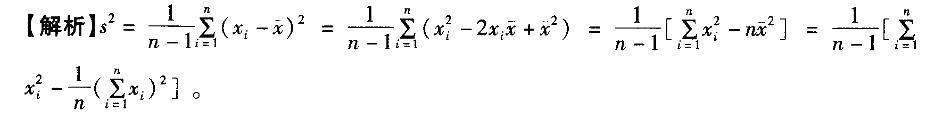

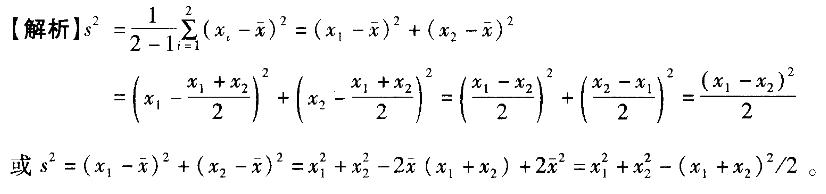

更多 “多元统计分析期末试题及答案” 相关考题
相关内容
最新试卷
热门试卷
- 2020-2021学年河北省邢台市高一下学期开学考试数学试题 解析版-
- 2020-2021学年河北省邢台市高一下学期开学考试政治试题-
- 2020-2021学年河北省秦皇岛一中高二第二学期开学考试物理试题 word版-
- 2020-2021学年河北省秦皇岛一中高二第二学期开学考试政治试题 word版-
- 2020-2021学年河北省秦皇岛一中高二第二学期开学考试化学试题 word版-
- 2020-2021学年河北省石家庄市第二中学高二下学期寒假作业总结体验化学试题 word版-
- 2020-2021学年河北省石家庄市六县市高一上学期期末联考政治试题-
- 2020-2021学年河北省石家庄市六县市高一上学期期末联考地理试题 Word版含解析-
- 2020-2021学年河北省石家庄市六县市高一上学期期末联考化学试题 Word版-
- 2020-2021学年河北省保定市高二上学期期末考试英语试题 解析版-
