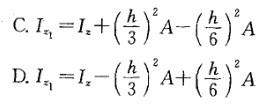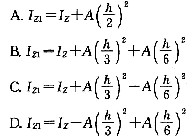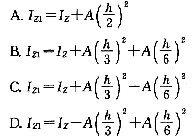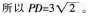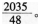考题
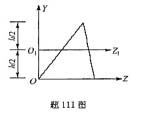
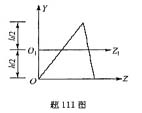
若已知如图所示三角形的面积A和惯性矩Iz，则下列结论正确的是( )。答案：D解析：设三角形的形心轴ZC与Z平行，则根据平行移动公式可得：
考题
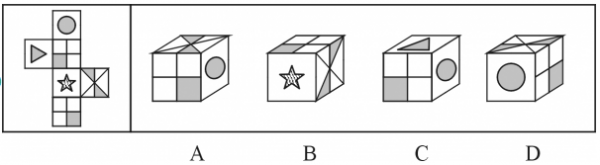
左边给定的是纸盒的外表面，下列哪一项能由它折叠而成?
A.如图
B.如上图
C.如上图示
D.如图所示答案：B解析：
相对面，不可能相邻，排除C。B项可由左侧图形折出。
考题
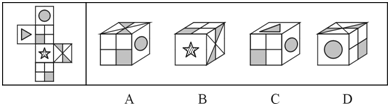
左边给定的是纸盒的外表面，下列哪一项能由它折叠而成?
A.如图
B.如上图
C.如上图示
D.如图所示答案：C解析：A项，假设正面和侧面正确，则顶面直角三角形方位错误；B项，右侧面中的对角线与正面中的阴影三角形不可能相交，错误；D项，对角线和中位线所在面应为相对面，不可能相邻，错误。选C。
考题
某位教师在讲完《相交线与平行线》这部分内容后，设计了一节《相交线与平行线》的复习课．在这节课中，他设计了如下一组题：
题1．如图3．BE平分∠ABD，DE平分∠BDC，且∠1+∠2=90。。
①BE与DE有什么样的位置关系 请说明理由。
②AB与CD有什么样的位置关系 请说明理由。
题2．如图4，AB∥CD且∠1+∠2=800：，求∠BED的度数。
题3．如图5，AB∥CD直线1交AB于点F、交CD于点G，点E是线段GF上的一点(点E
与点F、G不重合)，设∠ABC＝β,∠BED=γ。试探索a，β、γ之间的关系，并说明理由。
阅读上述教学设计片段，完成下列任务：
(1)从这组习题分析这节复习课的教学目标；(8分)
(2)分析这三道题的设计意图，并说明这组习题设计的特点；(10分)
(3)请你在图5的基础上，编一道类似习题，并给出答案。(12分) 答案：解析：(1)知识与技能目标：能够利用平行线的性质与判定定理，判断两条直线是否平行；能够利用两直线相交的性质求相交直线的交角度数。
过程与方法目标：学生通过对两直线的位置关系进行观察、猜想、探索等过程，初步形成几何直观，发展形象思维与抽象思维．锻炼合情推理和演绎推理能力，并能清晰地表达自己的想法。
情感态度与价值观目标：在学习过程中，体验获得成功的乐趣，锻炼克服困难的意志，建立自信心。养成认真勤奋、独立思考、合作交流、反思质疑等学习习惯，形成实事求是的科学态度。
(2)第一道题目，给出已知条件BE平分厶4BD，DE平分L_BDC且∠1+∠2=90。，通过两个问题引导学生思考，利用角平分线的性质，先判断出BE与DE的位置关系，进而利用两直线平行的判定定理判断AB与CD的位置。这道题目结合学生的已有知识经验，加深巩固对两直线平行判定定理的应用。为第三道题目的猜想做铺垫。
第二道题目．在第一道题目的基础之上对题目进行变形，已知AB∥CD且∠l+∠2=80。，结合对一道题目解题的经验，利用两直线平行的性质求出∠BED的度数。这道题目的主要设计意图为加深巩固学生对两直线平行的性质的应用，并为第三道题目的猜想做铺垫。
第三道题目。在前两道题目的铺垫下，将具体角变为抽象角，学生结合前两道题目的解题经验，进行猜想、探索证明。这道题目的主要设计意图为加深巩固学生对两直线平行的性质的应用，提高学生合情推理和演绎推理能力，将所学知识融会贯通。
三道题目逻辑联系紧密，考虑到学生的认知顺序，遵循由浅入深，由易到难，由表及里等一系列规律，让学生能够拾级而上，循序渐进，步步深入。以达到能够将所学知识灵活运用并初步形成几何直观，发展形象思维与抽象思维，锻炼合情推理和演绎推理能力的目的。
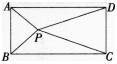
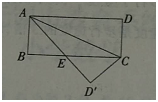
(3)如图5，直线l交AB于点F、交CD于点G，点E是线段GF上的一点(点E与点F、G不重合)，设∠ABE=01，∠CDE=fl，LBED=y。试探索γβα满足何条件的时候，AB与CD平行，并说明理由。
当a+B＝Y时，AB与CD平行。连接BD，因为三角形BDE的内角和为180度，所以∠EBD+∠EDB=1800一∠BDE，若β+α=γ，则∠EBD+∠EDB+α+β=1800～∠BED+α+β=1800，则AB与CD平行。
考题
若已知如图所示三角形的面积A和惯性矩Iz，则下列结论正确的是( )。答案：D解析：设三角形的形心轴ZC与Z平行，则根据平行移动公式可得：
考题
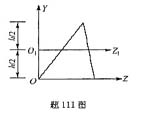
若已知如图所示三角形的面积A和惯性矩Iz，则下列结论正确的是( )。答案：D解析：设三角形的形心轴ZC与Z平行，则根据平行移动公式可得：
考题
初中数学《平行线的性质》一、考题回顾二、考题解析
【教学过程】
(一)导入新课
问：我们已经学习过平行线的哪些判定公理和定理?
学生齐答：1.同位角相等，两直线平行。2.内错角相等，两直线平行。3.同旁内角互补，两直线平行。
问：把这三句话颠倒每句话中的前后次序，能得到怎样的三句话?新的三句话还正确吗?
学生答：1.两直线平行，同位角相等。2.两直线平行，内错角相等。3.两直线平行，同旁内角互补。
教师指出：把一句原本正确的话，颠倒前后顺序，得到新的一句话，不能保证一定正确。例如，“对顶角相等”是正确的，倒过来说“相等的角是对顶角”就不正确了。因此，上述新的三句话的正确性，需要进一步证明。
(二)生成新知
平行线的性质一：
两条平行线被第三条直线所截，同位角相等。简单说成：两直线平行，同位角相等。怎样说明它的正确性呢?
平行线的性质二：
两条平行线被第三条直线所截，内错角相等。简单说成：两直线平行，内错角相等。启发学生，把这句话“翻译”成已知、求证，并作出相应的图形。已知：如图2-33，直线AB、CD被EF所截，AB∥CD，求证：∠3=∠2。1.随便说出4个数学中的基本事实?
2.如何检验学生对于知识的掌握?答案：解析：1.
①两点确定一条直线;
②两点之间线段最短;
③过一点有且只有一条直线与已知直线垂直;
④过直线外一点有且只有一条直线与这一条直线平行;
⑤同位角相等，两直线平行;
⑥两边及其夹角分别相等的两个三角形全等;
⑦两角及其夹边分别相等的两个三角形全等;
⑧三边分别相等的两个三角形全等;
⑨两条直线被一组平行线所截，所得的对应线段成比例。
2.
在这节课中，一方面，我通过引导学生与学生之间自己探讨，探讨后随机请学生代表发表对知识的理解，再结合老师的适时引导以及讲解，既可以考察学生对于知识的理解程度，又能帮助学生深刻的理解平行线的三条性质。另一方面，通过例题的形式检验学生对于知识的掌握，也帮助学生及时的应用所学知识，以达到巩固吸收的作用。最后一个方面，让学生以相互交流、相互启发的方式回顾课堂所学知识、总结收获，帮助学生提升对平行线三条性质的认识。
考题
左边给定的是纸盒的外表面，下列哪一项能由它折叠而成？A. 如图所示
B. 如图所示
C. 如图所示
D. 如图所示答案：A解析：利用时针法，椭圆面、斜线面与对角线面这三个相邻面的时针方向不同，排除A项。将最右边的对角线面移至最左边，利用描点法，B项正确。C项椭圆面、黑色面的公共相邻面应当是空白面，D项中黑色面与斜线面是相对面，不能同时出现。因此选B。
考题
下列四个图形中，与众不同的是：
A. 如图所示
B. ??如图所示??
C. ??如图所示??
D. ??如图所示??答案：C解析：考查位置类-静态位置，重点关注每幅图中相同元素的位置，仅有C项两个相同元素处在相邻的位置上，其他为相离。????
考题
左边给定的是纸盒的外表面，下列哪一项能由它折叠而成：
A. 如图所示
B. 如图所示
C. 如图所示
D. 如图所示答案：D解析：本题考查重构推理，A项中黑色正方形的位置应该在右上方，B项中右面中黑色三角形的位置出现错误，C项中圆形的位置应为五角星。因此，本题答案为D选项。
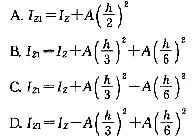
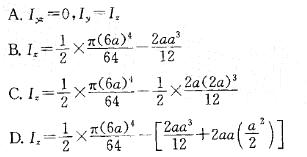
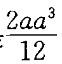，故结论B不正确。
