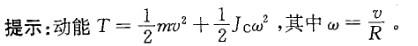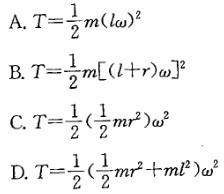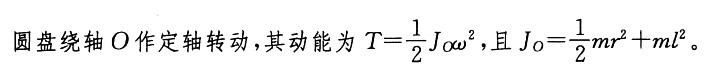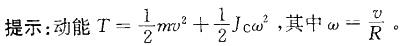智慧树全套答案单片机原理及其应用2020期末考试答案.docx
（本题8分）一质量为m的人造地球卫星，在环绕地球的圆形轨道上飞行，轨道半径为r0，地球质量为M，万有引力常数为G．
(1)求卫星的动能和万有引力势能之和；
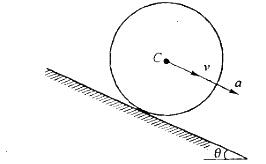
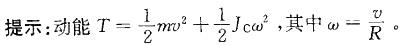
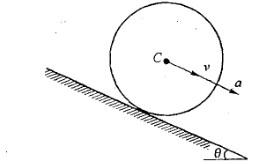
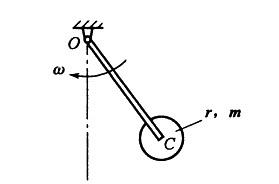
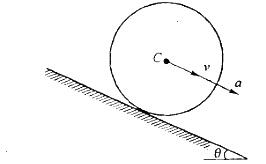
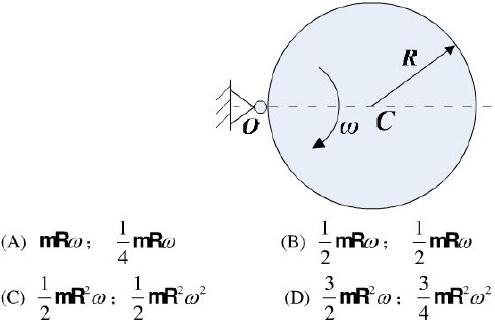
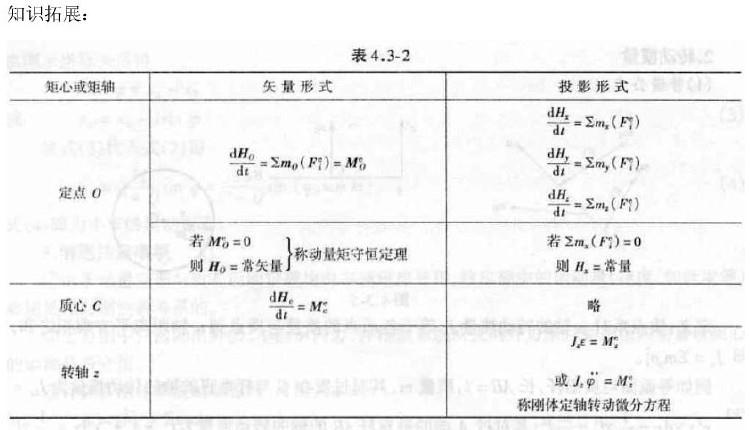
，其中Jc为刚体通过质心且垂直于运动平面
的轴的转动惯量。
此题中，
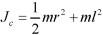，带入动能表达式，选（D）。
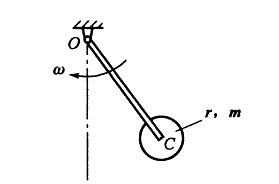
摘要:智慧树全套答案单片机原理及其应用2020期末考试答案学校：网课答案查询班级：V芯恭zhong號幻影校园姓名：幻影校园问：质量为M、半径为R的均质球体的引力势能（）。答：B问：质量为m、线长为l的单摆，可绕点O在竖直平面内摆动，初始时刻摆线被拉至水平，然后自由落下，则摆球到达水平点（O点正下方的点）时角速度的大小是（）。答：解：（1）摆球受力如图3-13所示。摆线的张力通过点O，因此其力矩为零；重力p对点O产生力矩，其大小为可见M随角而变化，其方向垂直纸面向里。由角动量定理，得又，代入上式，并积分，得摆线与水平线成角时，摆球对点O的角动量为（2）当摆球摆到B时，，因此摆球角动量摆球到达B时角速度的大小问：质量为m=10g的子弹，以v=200m/s的速度射入木块。木块的阻力平均值为5000.则子弹射入的深度为（）。答：0.04m问：质量为m=10g的子弹，以v=200m/s的速度射入木块。木块的阻力平均值为5000.则阻力做的功为（）。 答：200J问：质量为M=500Kg、长L=4m的木船浮在静止水面上，一质量m=50kg的人站在船尾。今人以时快时慢的不规则速率从船尾走到船头，设船与水之间的摩擦可以忽略，则船相对于岸移动了多少？（）答：-4/11m问：质量为M=980g的木块静止在光滑水平面上，一质量为m=20g的子弹以v=800m/s的速率水平地射入木块后与木块一起运动,则耗散的机械能为（）。答：C问：质量为M=980g的木块静止在光滑水平面上，一质量为m=20g的子弹以v=800m/s的速率水平地射入木块后与木块一起运动,则木块施于子弹的力对子弹所作的
