高考理科数学选择填空题练习之集合与简易逻辑含解析
已知集合A={x|x≤1},B={x|≥a},且A∪B=R，
则实数a的取值范围是__________________.
2.ɑ≤1
使用运算符测试集合包含集合A是否为集合B的真子集的表达式可以写作_______。
设Y表示集合的并运算，I表示集合的交运算，
表示集合A的绝对补，A-B月表示集合A与B的差，则A-B=______。
A．AY(AIB)
B．AY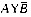
C．AI(AYB)
D．AI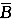
解析：设任意2个集合A和B，所有属于A而不属于B的一切元素组成的集合S，称作B对于A的差集(或相对补)，记作S=A-B。设E为全集，对任一集合A关于E的补E- A，称为A的绝对补。根据这个定义，显然A-B=A∩
。
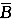求两个集合A和B的差集是指在A中删除A和B中共有的元素，即删除链表中的相应结点,所以要保存待删除结点的前驱，使用指针pre指向前驱结点。pa和pb分别是链表La和Lb的工作指针,初始化为相应链表的第一个结点，从第一个结点开始进行比较，当两个链表La和Lb均为到达表尾结点时，如果La表中的元素小于Lb表中的元素，pre置为La表的工作指针pa删除Lb表中的元素;如果其中一个表中的元素较小时，删除此表中较小的元素，此表的工作指针后移。当链表La和Lb有一个为空时，依次删除另一个非空表中的所有元素。
[算法描述]
void Difference(LinkList& La, LinkList& Lb,int *n)
{∥差集的结果存储于单链表La中，*n是结果集合中元素个数，调用时为0
pa=La->next; pb=Lb->next;
∥pa和pb分别是链表La和Lb的工作指针,初始化为相应链表的第一个结点
pre=La; ∥pre为La中pa所指结点的前驱结点的指针
while(pa&&pb)
{if(pa->data
∥ A链表中当前结点指针后移
else if(pa->data>q->data)q=q->next; ∥B链表中当前结点指针后移
else {pre->next=pa->next; ∥处理A，B中元素值相同的结点，应删除
u=pa; pa=pa->next; delete u;} ∥删除结点
}
}
设∪表示集合的并运算，∩表示集合的交运算，
表示集合A的绝对补， A-B表示集合A与B的差，则A-B=(55)。
A．A∪(A∩B)
B．A∪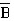
C．A∩(A∪B)
D．A∩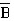
解析：设任意两个集合A和B，所有属于A而不属于B的一切元素组成的集合S，称做B对于A的差集(或相对补)，记作S=A-B。设E为全集，对任一集合A关于E的补E-A，称为A的绝对补。根据这个定义，显然A-B=A∩。
集合与简易逻辑一、选择题12018盱眙中学已知全集，集合，集合，则集合（ ）ABCD22018洪都中学已知全集，集合，则图中阴影部分表示的集合为（ ）ABCD32018八一中学集合的真子集的个数是（ ）A9B8C7D642018洪都中学已知集合，若，则实数的取值范围为（ ）ABCD52018唐山摸底命题“，”的否定是（ ）A，B，C，D， 62018静宁县一中已知、都是实数，那么“”是“”的（ ）A充分不必要条件B必要不充分条件C充分必要条件D既不充分也不必要条件72018大同中学已知，下列四个条件中，使成立的必要而不充分的条件是（ ）ABCD82018静宁县一中下列说法错误的是（ ）A对于命题，则，B“”是“”的充分不必要条件C若命题为假命题，则，都是假命题D命题“若，则”的逆否命题为：“若，则”92018甘肃模拟，则（ ）ABCD102018辽宁联考已知集合，则能使成立的实数的取值范围是（ ）ABCD112018曲靖一中命题：“，不等式成立”；命题：“函数的单调递增区间是”，则下列复合命题是真命题的是（ ）ABCD122018长春外国语已知集合，则的子集个数为（ ）A3B4C7D8二、填空题132018哈尔滨期末，则_142018浦东三模已知集合，则_152018甘谷县一中已知集合，若，求实数的取值范围_162018清江中学 “”是“函数的图象关于轴对称”的_条件（填“充分必要”、“充分不必要”、“必要不充分”、“既不充分也不必要”）答案与解析一、选择题1【答案】B【解析】，则；故选B2【答案】A【解析】全集，集合，图中阴影部分表示的集合为，故选A3【答案】C【解析】时，；时，；时，；时，；函数在上是减函数，当时，；，共3个元素，根据公式可得其真子集的个数为个，故选C4【答案】B【解析】，作出图形如下：，故选B5【答案】B【解析】由全称命题与存在性命题的关系，可得命题“，”的否定是“，”，故选B6【答案】B【解析】，有可能为0，故不能推出，反过来，则成立，故为必要不充分条件故选B7【答案】A【解析】“”能推出“”，故选项A是“”的必要条件，但“”不能推出“”，不是充分条件，满足题意；“”不能推出“”，故选项B不是“”的必要条件，不满足题意；“”不能推出“”，故选项C不是“”的必要条件，不满足题意；“”能推出“”，且“”能推出“”，故是充要条件，不满足题意；故选A8【答案】C【解析】根据全称命题的否定是特称命题知A正确；由于可得，而由得或，“”是“”的充分不必要条件正确；命题为假命题，则，不一定都是假命题，故C错；根据逆否命题的定义可知D正确，故选C9【答案】A【解析】，则故选A10【答案】C【解析】，故选C11【答案】A【解析】由题意，命题：“，不等式成立”；根据指数函数与对数函数的图象可知是不正确的，命题为假命题；命题：“函数的单调递增区间应为”，为假命题，为真命题，故选A12【答案】D【解析】集合，中含有3个元素，集合的子集个数有，故选D二、填空题13【答案】【解析】，14【答案】【解析】集合，故答案为15【答案】【解析】，（1），即，解得，（2），即，解得，综上所述，实数的取值范围为故答案为16【答案】充分不必要【解析】若函数的图象关于轴对称，则，必要性不成立，若，则函数的图象关于轴对称充分性成立，“”是“函数的图象关于轴对称”的充分不必要条件；故答案为充分不必要
设∪表示集合的并运算，∩表示集合的交运算，A表示集合A的绝对补，A-B表示集合A与B的差，则A-B=______ 。
A．A∪(A∩B)
B．A∪B
C．A∩(A∪B)
D．A∩B
解析：由集合定义及运算性质可知D正确。
（ ）
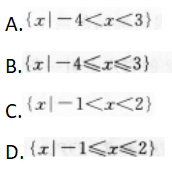
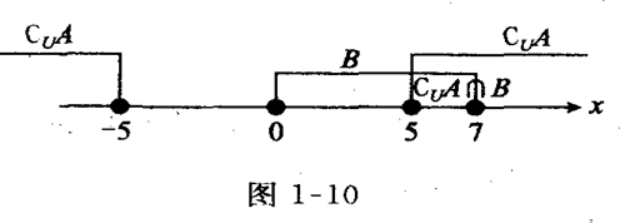
B.5个
C.6个
D.7个