若浮点数用原码表示，则判断运算结果为规格化数的方法是()。A.阶符与数符相同 B.阶符与数符相异 C.尾数最高数值位为1 D.尾数符号与尾数最高数值位不相同

题目
若浮点数用原码表示，则判断运算结果为规格化数的方法是()。

A.阶符与数符相同
B.阶符与数符相异
C.尾数最高数值位为1
D.尾数符号与尾数最高数值位不相同
相似考题

1.● 浮点数的一般表示形式为N＝2E×F，其中E为阶码，F为尾数。以下关于浮点表示的叙述中，错误的是（3）。两个浮点数进行相加运算，应首先（4）。（3）A. 阶码的长度决定浮点表示的范围，尾数的长度决定浮点表示的精度B. 工业标准IEEE754浮点数格式中阶码采用移码、尾数采用原码表示C. 规格化指的是阶码采用移码、尾数采用补码D. 规格化表示要求将尾数的绝对值限定在区间[0.5, 1)（4）A. 将较大的数进行规格化处理B. 将较小的数进行规格化处理C. 将这两个数的尾数相加D. 统一这两个数的阶码

2.浮点数规格化的目的是()A、便于运算B、多此一举C、使数的浮点表示是唯一的D、使长度最短

3.若浮点数用补码表示，则判断运算结果是否为规格化数的方法是A.阶符与数符相同B.阶符与数符相异C.数符与尾数小数点后第一位数字相异D.数符与尾数小数点后第一位数字相同

4.若浮点数的阶码用移码表示,尾数用补码表示。两规格化浮点数相乘,最后对结果规格化时,右规的右移位数最多为()位。A.1B.2C.尾数位数D.尾数位数-1

更多“若浮点数用原码表示，则判断运算结果为规格化数的方法是()。”相关问题

  • 第1题：

    浮点数的一般表示形式为N=2E×F，其中E为阶码，F为尾数。以下关于浮点表示的叙述中，错误的是( )。两个浮点数进行相加运算，应首先( )。

    A．阶码的长度决定浮点表示的范围，尾数的长度决定浮点表示的精度

    B．工业标准IEEE754浮点数格式中阶码采用移码、尾数采用原码表示

    C．规格化指的是阶码采用移码、尾数采用补码

    D．规格化表示要求将尾数的绝对值限定在区间[O．5，1)


    正确答案：C
    解析：在浮点数中，为了在尾数中表示最多的有效数据位，同时使浮点数具有唯一的表示方式，浮点数的编码应当采用一定的规范，规定尾数部分用纯小数给出，而且尾数的绝对值应大于或等于l／R，并小于或等于1，即小数点后的第一位不为零。这种表示的规范称为浮点数的规格化的表示方法。两个符点数相加，首先应统一它们的阶码。对阶时…总是小阶向大阶对齐，即小阶的位数向右移位。

  • 第2题：

    下面关于浮点数规格化的叙述中，正确的是

    A.A.高浮点数的精度

    B.B.使浮点数的表示格式一致

    C.C.浮点数的尾数左移实现的规格化叫左规

    D.D.浮点数的尾数右移实现的规格化叫右规

    E.E.判断补码表示的数和原码表示的数是否规格化的方法一样


    正确答案：ACD

  • 第3题：

    一个12位浮点数100010111111，从高位到低位依次为阶符1位、阶码3位(用补码表示)、数符位、尾数7位(用补码表示)，则该数是______。

    A．非规格化、绝对值最小的负数

    B．离原点最近的规格化负数

    C．离原点最远的规格化负数

    D．非规格化、绝对值最大的负数


    正确答案：B
    解析：阶符1位为1表示负，阶码3位000(补码)为0，故阶的部分位20=1；数符1位为1表示负，尾数用补码表示为10111111，其原码为11000001，真值为-(2-1+2-7)，绝对值大于0.5小于1，是规格化的负数。由于尾数是用补码表示，数符后面一位必须为0，可以表示的最大的规格化负数为-(2-1+2-7)，也就是说(2-1+2-7)是规格化负数中离原点最近的数。

  • 第4题：

    计算机中十六位浮点数的表示格式为

    某机器码为1110001010000000，

    若阶码为移码且尾数为反码，则其十进制真值为(7)；

    若阶码为移码且尾数为原码，则其十进制真值为(8)；

    若阶码为补码且尾数为反码，则其十进制真值为(9)；

    若阶码为补码且尾数为原码．则其十进制真值为(10)，将其规格化后的机器码为(11)。

    A．0.078125

    B．20

    C．20.969375

    D．1.25


    正确答案：B
    解析：(7)如果阶码为移码，由于阶码是4位二进制整数，设真值为X，根据整数移码定义：[X]移码=23+X(1110)2=(14)10，可求得阶码真值为6。如果尾数为反码，从符号位可判断尾数是正数，根据小数反码定义，正小数的反码就是其自身，可求得尾数的真值为：(0.01010000000)2=(2-1+2-4)=(0.3125)10，根据浮点数定义，该机器码真值为0.3125*26=20。(8)如果阶码为移码，同上，真值为6。如果尾数是原码，从符号位可判断尾数是正数，根据小数原码定义，正小数的原码就是其本身，可求得尾数的真值为0.3125。由此可知该机器码真值也是20。(9)如果阶码为补码，由于阶码是4位二进制整数，从符号位判断为负数，设真值为X，根据负整数定义[X]补码=24+X=(1110)2=(14)10，求得阶码的真值为-2。如果尾数为反码，同(7)一样求出尾数的真值为0.3125。这样，该机器码真值为0.3125*2-2=0.078125。(10)如果阶码是补码，尾数是原码，求出阶码和尾数的真值分别为-2和0.3125，这样该机器码的真值也是0.078125。(11)对浮点数进行规格化处理，规定浮点数的尾数部分用纯小数形式表示，当尾数的值不为0时，其绝对值应大于或等于0.5，用二进制表示为0.1XXX…XX(X为0或1)。对于不符合这一规定的浮点数，可改变阶码的大小并同时用左右移尾数的方法来满足这一规定。显然尾数0.01010000000不合要求，应左移1位，而阶码则应相应地减1，因此规格化处理后的阶码为1101，尾数为010100000000。

  • 第5题：

    若单精度浮点数用32位二进制数表示，其中最高位为符号位，后面跟8位经偏移的阶码移码，偏移量为+127。尾数用原码表示，且把尾数规格化为1.xxx...x(x为0或1)，并将1去掉，尾数用23位表示。根据该标准，十进制数-178.125的规格化表示形式为(110)。

    A．110000110 01100100010000000000000

    B．110000111 01100100010000000000000

    C．0 10000100 01100100010000000000000

    D．1 10000110 11100100010000000000000


    正确答案：A
    解析：在浮点数系统中，小数点的浮动使数值的表示不能惟一，从而给数据处理带来困难，因此有必要使浮点数的表示与存储有一定的标准，考虑到阶码、尾数之间的关系，常将尾数的量高数字位变成有效值，此过程称为规格化(normalization)。规格化-178.125的步骤如下：先将-178.125变换成二进制得到-10110010.001，将小数点左移7位进行规格化，然后加127后得到移码10000110，于是我们得到规格化后的二进制数为1106410110011001000100000000000000。

  • 第6题：

    计算机中十六位浮点数的表示格式为图1.4

    某机器码为1010001010000000。

    若阶码为移码且尾数为反码，则其真值为(60)；

    若阶码为移码且尾数为原码，则其真值为(61)；

    若阶码为补码且尾数为反码，则其真值为(62)；

    若阶码为补码且尾数为原码，则其真值为(63)，将其规格化后的机器码为(64)。

    A．0.00000001012

    B．2010

    C．1.2510

    D．20.96937510


    正确答案：C

  • 第7题：

    如果浮点数的尾数用补码表示，则( )是规格化的数。

    A.1.01000
    B.1.11110
    C.0.01001
    D.1 11001

    答案：A
    解析：
    本题考查计算机系统硬件基础知识。
    一个含小数点的二进制数Ⅳ可以表示为更一般的形式：
    N=2E×F
    其中E称为阶码，F为尾数，这种表示数的方法称为浮点表示法。
    在浮点表示法中，阶码通常为带符号的纯整数，尾数为带符号的纯小数。浮点数的表示格式如下：

    很明显，一个数的浮点表示不是唯一的。当小数点的位置改变时，阶码也相应改变，因此可以用多种浮点形式表示同一个数。
    为了提高数据的表示精度，当尾数的值不为0时，规定尾数域的最高有效位应为1，这称为浮点数的规格化表示。否则修改阶码同时左移或右移小数点的位置，使其变为规格化数的形式。规格化就是将尾数的绝对值限定在区间[0.5，1)。
    尾数用补码表示时，[+0.5，1)之间的数表示形式为0.1******，而(-1.0，-0.5)之间的数则表示为1.0******。由于[-0.5]补=1.1000000，[-1.0]补=1.0000000，因此将(-1.0，-0.5]扩展为[-1.0，-0.5)，从而便于通过判断符号位和小数点后的最高位是否相异来判断尾数是否为规格化形式。

  • 第8题：

    若浮点数用补码表示，则判断运算结果为规格化数的方法是()。

    A.阶符与数符相同为规格化数
    B.阶符与数符相异为规格化数
    C.数符与尾数小数点后第一位数字相异为规格化数
    D.数符与尾数小数点后第一位数字相同为规格化数

    答案：C
    解析：
    根据补码表示规则，当数符与尾数小数点后第一位相异时为规格化数，而阶码与数符和规格化与否无关。

  • 第9题：

    如果浮点数用补码表示，则判断下列哪一项的运算结果是规格化数（）。

    • A、1.11000
    • B、0.01110
    • C、1.00010
    • D、0.01010

    正确答案:C

  • 第10题：

    单选题
    若浮点数用补码表示，则判断运算结果为规格化数的方法是（）。
    A

    阶符与数符相同，则为规格化数

    B

    小数点后第一位为1，则为规格化数

    C

    数符与小数点后第一位数字相异，则为规格化数

    D

    数符与小数点后第一位数字相同，则为规格化数


    正确答案： C
    解析： 暂无解析

  • 第11题：

    单选题
    若浮点数的阶码用移码表示，尾数用补码表示。两规格化浮点数相乘，最后对结果规格化时，右规的右移位数最多为（）位。
    A

    1  

    B

    2  

    C

    尾数位数  

    D

    尾数位数-1


    正确答案： D
    解析： 暂无解析

  • 第12题：

    单选题
    下列关于IEEE 754浮点数格式的叙述中，正确的是（　　）。
    A

    尾数和阶码均用原码表示

    B

    尾数用补码表示、阶码用原码表示

    C

    只能表示规格化数

    D

    可以表示规格化数和非规格化数


    正确答案： C
    解析：
    IEEE 754的浮点格式既可以表示规格化数，也可以表示非规格化数，同时，指数部分采用移码表示，尾数部分采用原码表示。

  • 第13题：

    设置某计算机浮点数运算结果为：阶码1010，尾码10110101(各自均有1bit符号位占最高位)，设它们均用补码表示的，则此数规格化后的阶码为______。


    正确答案：1020
    1020

  • 第14题：

    计算机内采用规格化浮点数表示，阶码用移码表示(最高位代表符号位)，尾数用原码表示。(1)表示不是规格化浮点数。 阶码 尾数

    A．1111111 1.1000......00

    B．0011111 1.0111......01

    C．1000001 0.1111......01

    D．0111111 0.1000......10


    正确答案：B
    解析：对于规格化的浮点数，尾数有三种形式：0.1xx……x(原码、补码、反码都是正数的形式)1.0XX……X(补码、反码是负数的形式)1.1xx……X(原码是负数的形式)尾数用原码表示，B是不符合规格化的形式。

  • 第15题：

    设机器中浮点数的格式如下：

    其中阶码6位，包括1位符号位，尾数10位(含1位数符)，浮点数的基为2。阶码用补码表示，尾数用原码表示。对于十进制数-25.8375，当阶码用补码表示、尾数用原码表示时，得到的规格化机器码为(38)；当阶码用移码表示、尾数用原码表示时，得到的规格化机器码为(39)；当阶码用原码表示，尾数用补码表示时，得到的规格化机器码为(40)。

    A．1001011100111000

    B．1110101100111010

    C．1001011000111010

    D．1001011100111010


    正确答案：A

  • 第16题：

    下面是机器中浮点数的表示格式：

    设浮点数的基为2。若阶码用补码表示、尾数用原码表示，十进制数-51.875采用上述格式可表示为(7)；若阶码用移码表示、尾数用补码表示，该数可表示为(8)。

    A．0110 111001111100

    B．0110 011001111100

    C．0110 001110011111

    D．0101 011001111100


    正确答案：A
    解析：首先将-51.875转换为二进制表示：(-51.875)10=-110011.111=-0.110011111×2110，其中110是阶码，-0.110011111是尾数(绝对值大于0.5)。由于规格化表示格式中阶符和阶码共计4位，本题中阶码大于0，故采用补码时，这4位应该是[110]补=[110]原=0110。而采用原码表示尾数时，向[-0.110011111]原=1110011111后面添零补足12位，得111001111100。

  • 第17题：

    若浮点数用补码表示，判断结果是否为规格化数的方法是(10)。

    A．阶符与数符相同

    B．阶符与数符相异

    C．数符与尾数最高有效位相异

    D．数符与尾数最高有效位相同


    正确答案：C
    解析：本题考查浮点数的规格化。规格化的浮点数形式分为尾数和阶码两部分。将数表示成规格化的浮点数形式时，需要事先规定尾数和阶码的位数及采用的编码方式，题目中说明是用补码表示，在用补码表示时，判定结果是否为规格化数的方法是判断数符与尾数最高有效位是否相同，如果相同，则不是规格化数；如果不同，则是规格化数。

  • 第18题：

    如果浮点数的尾数用补码表示，则(20)是规格化的数。

    A.1.0l000

    B.1.11110

    C. 0.01001

    D.1.11001


    正确答案：A
    本题考查计算机系统硬件基础知识。一个含小数点的二进制数N可以表示为更一般的形式：其中E称为阶码，F为尾数，这种表示数的方法称为浮点表示法。在浮点表示法中，阶码通常为带符号的纯整数，尾数为带符号的纯小数。浮点数的表示格式如下：很明显，一个数的浮点表示不是唯一的。当小数点的位置改变时，阶码也相应改变，因此可以甩多种浮点形式表示同一个数。为了提高数据的表示精度，当尾数的值不为0时，规定尾数域的最高有效位应为1，这称为浮点数的规格化表示。否则修改阶码同时左移或右移小数点的位置，使其变为规格化数的形式。规格化就是将尾数的绝对值限定在区间[0.5，1）。尾数用补码表示时，[+05，1）之间的数表示形式为0.1*****,而(-1.0，-05)之间的数则表示为1.0******。由于[-0.5]*=1.1OOOOOO，[-0.1]*=1.0000000，因此将(-0.1，一05]扩展为[-1.O，-0.5)，从而便于通过判断符号位和小数点后的最高位是否相异来判断尾数是否为规格化形式。

  • 第19题：

    设32位浮点数格式如下。以下关于浮点数表示的叙述中，正确的是（ ）。若阶码采用补码表示，为8位（含1位阶符），尾数采用原码表示，为24位（含1位数符），不考虑规格化，阶码的最大值为（请作答此空）。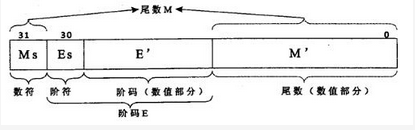

    A.255
    B.256
    C.127
    D.128

    答案：C
    解析：
    本题考察计算机数据的表示。浮点数所能表示的数值范围主要由阶码决定，所表示数值的精度则由尾数决定。八位阶码的最大值为127。

  • 第20题：

    某浮点数格式如下：7 位阶码（包含一个符号位），9 位尾数（包含一个符号位）。若阶码用移码、尾数用规格化的补码表示，则浮点数所能表示数的范围是（）。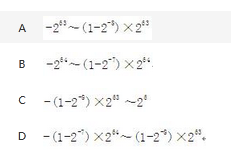


    答案：A
    解析：
    浮点数所能表示的数值范围如下：最大的正数

  • 第21题：

    若浮点数的阶码和尾数都用补码表示，则判断运算结果是否为规格化数的方法是（）。

    • A、阶符与数符相同为规格化数
    • B、阶符与数符相异为规格化数
    • C、数符与尾数小数点后第一位数字相异为规格化数
    • D、数符与尾数小数点后第一位数字相同为规格化数

    正确答案:C

  • 第22题：

    问答题
    设某浮点数格式为：字长12位，阶码6位，用移码表示，尾数6位，用原码表示，阶码在前，尾数（包括数符）在后，则按照该格式：已知X=-25/64，Y=2.875，求数据X、Y的规格化的浮点数形式。

    正确答案： [X]=-0.011001=-0.11001*2-1
    X.的符号：1
    X.的阶码：-1=-00001=（移码）011111
    X.的尾数：11001
    解析： 暂无解析

  • 第23题：

    单选题
    如果浮点数用补码表示，则判断下列哪一项的运算结果是规格化数（）。
    A

    1.11000

    B

    0.01110

    C

    1.00010

    D

    0.01010


    正确答案： B
    解析： 暂无解析

相关内容