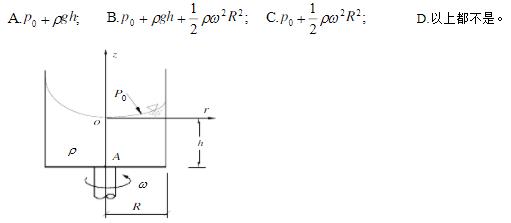如图所示圆环以角速度ω绕铅直轴AC自由转动,圆环的半径为R,对转轴的转动惯量为I;在圆环中的A点放一质量为m的小球,设由于微小的干扰,小球离开A点。忽略一切摩擦,则当小球达到B点时,圆环的角速度是( )。
题目
如图所示圆环以角速度ω绕铅直轴AC自由转动,圆环的半径为R,对转轴的转动惯量为I;在圆环中的A点放一质量为m的小球,设由于微小的干扰,小球离开A点。忽略一切摩擦,则当小球达到B点时,圆环的角速度是( )。

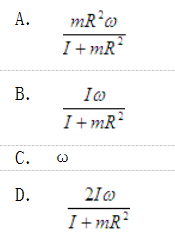

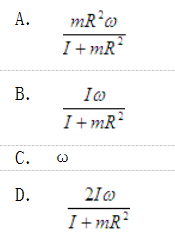
相似考题
更多“如图所示圆环以角速度ω绕铅直轴AC自由转动,圆环的半径为R,对转轴的转动惯量为I;在圆环中的A点放一质量为m的小球,设由于微小的干扰,小球离开A点。忽略一切摩擦,则当小球达到B点时,圆环的角速度是( )。 ”相关问题
-
第1题:
均质圆柱体半径为R,质量为m,绕关于对纸面垂直的固定水平轴自由转动,初瞬时静止(G在O轴的铅垂线上),如图所示。则圆柱体在位置θ=90°时的角速度是( )。
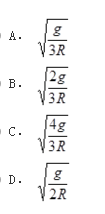 答案:C解析:
答案:C解析:
-
第2题:
忽略质量的细杆OC=l,其端部固结匀质圆盘圆心,盘质量为m,半径为r。系统以角速度w绕轴O转动。系统的动能是: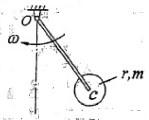
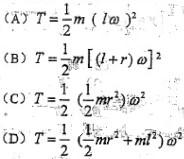 答案:D解析:此为定轴转动刚体,动能表达式为
答案:D解析:此为定轴转动刚体,动能表达式为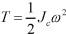 ,其中Jc为刚体通过质心且垂直于运动平面
,其中Jc为刚体通过质心且垂直于运动平面
的轴的转动惯量。
此题中,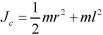 ,带入动能表达式,选(D)。
,带入动能表达式,选(D)。 -
第3题:
如图,半径为R的圆轮以匀角速度作纯滚动,带动AB杆绕B作定轴转动,D是轮与杆的接触点,如图所示。若取轮心C为动点,杆BA为动坐标系,则动点的牵连速度为( )。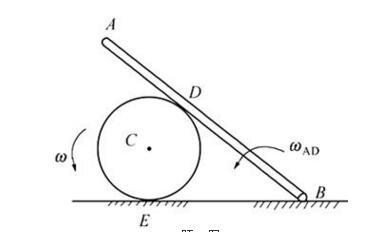
 答案:C解析:
答案:C解析:
-
第4题:
水平管以角速度w绕铅垂轴Z转动。管内有一小球M以速度V=rw沿管运动,r为小球到转轴的距离。球M的绝对速度是( )。

 答案:C解析:
答案:C解析: -
第5题:
图示均质圆轮,质量为m,半径为r,在铅垂图面内绕通过圆轮中心O的水平轴以匀角速度ω转动。则系统动量、对中心O的动量矩、动能的大小为: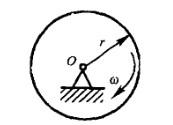
 答案:A解析:提示:根据动量、动量矩、动能的定义,刚体做定轴转动时p=mvc, LO=JOω,T=1/2JOω2。
答案:A解析:提示:根据动量、动量矩、动能的定义,刚体做定轴转动时p=mvc, LO=JOω,T=1/2JOω2。 -
第6题:
忽略质量的细杆OC=l,其端部固结匀质圆盘。杆上点C为圆盘圆心。盘质量为m,半径为r。系统以角速度ω绕轴O转动。系统的动能是: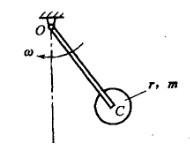
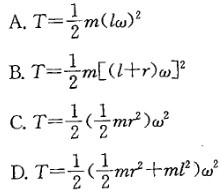 答案:D解析:提示:圆盘绕轴O作定轴转动,其动能为T=1/2JOω2。
答案:D解析:提示:圆盘绕轴O作定轴转动,其动能为T=1/2JOω2。 -
第7题:
在Oyz平面内有一半径为R的圆环,均匀带有电荷量q,试计算圆环轴线(ox轴)上任意一点P处的电场强度及电势的大小。
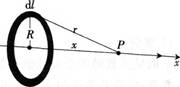 答案:解析:
答案:解析:

-
第8题:
图示一半径为R的圆柱形容器,内盛有密度为ρ的液体,若容器以等角速度ω绕OZ轴旋转,则A点的压强为()
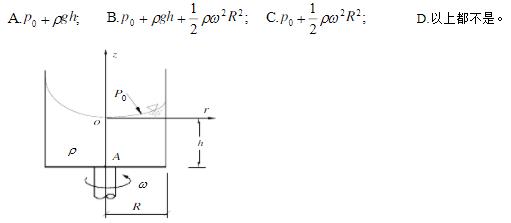
AA
BB
CC
DD
A
略 -
第9题:
设质量分布均匀的圆柱体的质量为m,半径为R,绕中心旋转时的角速度为ω,则圆柱体的转动惯量为()。
- A、mR2
- B、mR2/2
- C、mRω
正确答案:B -
第10题:
一半径为R的均匀带电圆环,电荷线密度为λ设无穷远处为电势零点,则圆环中心O点的电势U=()
正确答案:λ/(2ε0) -
第11题:
均匀带电圆环带电量q,圆环半径为R,则圆环中心点处的电场强度大小为()。
正确答案:0 -
第12题:
单选题质量为2m,半径为R的偏心圆板可绕通过中心O的轴转动,偏心距OC= 。在OC连线上的A点固结一质量为m的质点,OA=R如图示。当板以角速度w绕轴O转动时,系统动量K的大小为()。(注:C为圆板的质心)。AK=0
BK=mRw
CK=mRw
DK=2mRw
正确答案: A解析: 暂无解析 -
第13题:
忽略质量的细杆OC=l,其端部固结匀质圆盘。杆上点C为圆盘圆心。盘质量为m,半径为r。系统以角速度ω绕轴O转动,如图所示。系统的动能是: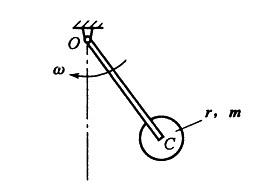
 答案:D解析:
答案:D解析: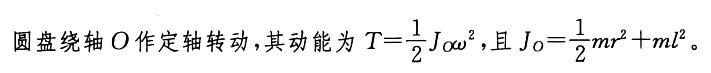
-
第14题:
均质圆柱体半径为R,质量为m,绕与纸面垂直的固定水平轴自由转动,初瞬时静止(θ=0°),如图所示,则圆柱体在任意位置θ时的角速度是( )。
 答案:B解析:
答案:B解析:
-
第15题:
如图所示,曲柄OA长R,以匀角速度ω绕O轴转动,均质圆轮B在水平面上做纯滚动,其质量为m,半径为r。在图示瞬时,OA杆铅直。圆轮B对接触点C的动量矩为( )mRrω。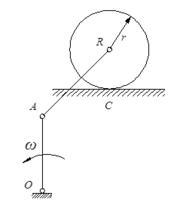 A.0.5
A.0.5
B.1.0
C.1.5
D.2.0答案:B解析:图示瞬时,点A和点B的速度方向均沿水平方向, AB杆作平动,圆轮B的轮心速度
-
第16题:
如图所示圆环以角速度ω绕铅直轴AC自由转动,圆环的半径为R,对转轴的转动惯量为I;在圆环中的A点放一质量为m的小球,设由于微小的干扰,小球离开A点。忽略一切摩擦,则当小球达到B点时,圆环的角速度是( )。

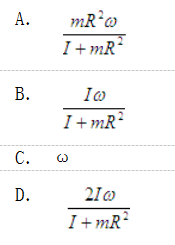 答案:B解析:
答案:B解析:
-
第17题:
均质细直杆OA长为l ,质量为m,A端固结一质置为m的小球(不计尺寸),如图所示。当OA杆以匀角速度w绕O轴转动时,该系统时O轴的动量矩为: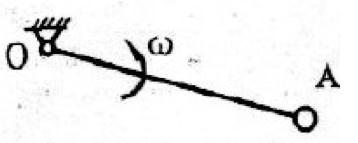
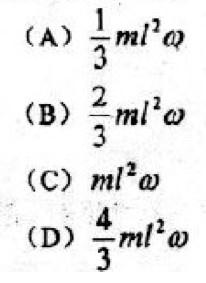 答案:D解析:
答案:D解析:
-
第18题:
如图所示,半径为R的光滑圆环竖直放置,环上套有质量分别为m和2m的小球A和B。A、B之间用一长为/2R的轻杆相连。开始时A在圆环的最高点,现将A、B静止释放,则( )。 A.B球从开始运动至到达圆环最低点的过程中.杆对B球所做的总功不为零
A.B球从开始运动至到达圆环最低点的过程中.杆对B球所做的总功不为零
B.A球运动到圆环的最低点时.速度为零
C.B球可以运动到圆环的最高点
D.在A、B运动的过程中,A、B组成的系统机械能守恒答案:D解析:
误;设B球到右侧最高点时,OB与竖直方向的夹角为0,圆环圆心处为势能零点.则由系统机械能守恒可得:mAgR=mBgRcosθ—magRsinθ,代人数据得θ:37。B球不能运动到最高点.故C项错误。在A、B运动的过程中,A、B组成的系统只有重力做功,机械能守恒,故D项正确。 -
第19题:
图4-67示均质圆轮,质量为m,半径为r,在铅垂图面内绕通过圆轮中心O的水平轴以匀角速度ω转动。则系统动量、对中心O的动量矩、动能的大小为( )。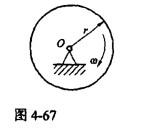
 答案:A解析:提示:根据动量、动量矩、动能的定义,刚体作定轴转动时,ρ = mvc、LO= JOω, T=1/2JOω2。
答案:A解析:提示:根据动量、动量矩、动能的定义,刚体作定轴转动时,ρ = mvc、LO= JOω, T=1/2JOω2。 -
第20题:
在用三线摆测转动惯量实验中,是如何测出圆环的转动量的?在m0示圆环的质量,r内、r外分别表示圆环的半径,它的转动量理论值(绕中心)是什么?
正确答案:先测带孔圆盘的转动惯量。再测带孔圆盘与圆环的转动惯量圆环的转动惯量为I1=I0-I -
第21题:
一飞轮以角速度ω0绕光滑固定轴旋转,飞轮对轴的转动惯量为J1;另一静止飞轮突然和上述转动的飞轮啮合,绕同一转轴转动,该飞轮对轴的转动惯量为前者的二倍,啮合后整个系统的角速度ω=()。
正确答案:(1/3)ω0 -
第22题:
均质圆环的质量为m,半径为R,圆环绕O轴的摆动规律为φ=ωt,ω为常数。图4-74所示瞬时圆环对转轴O的动量矩为()。
- A、mR2ω
- B、2mR2ω
- C、3mR2ω
正确答案:B -
第23题:
单选题均质圆环的质量为m,半径为R,圆环绕O轴的摆动规律为φ=ωt,ω为常数。图4-74所示瞬时圆环对转轴O的动量矩为()。AmR2ω
B2mR2ω
C3mR2ω
正确答案: C解析: 暂无解析 -
第24题:
单选题设质量分布均匀的圆柱体的质量为m,半径为R,绕中心旋转时的角速度为ω,则圆柱体的转动惯量为()AmR2;
BmR2/2;
CmRω。
正确答案: C解析: 暂无解析