某周期为T的非正弦周期信号分解为傅里叶级数时,其三次谐波的角频率为300πrad/s,则该信号的周期T为( )s。A.50 B.0.06 C.0.02 D.0.05
题目
B.0.06
C.0.02
D.0.05
相似考题
参考答案和解析
更多“某周期为T的非正弦周期信号分解为傅里叶级数时,其三次谐波的角频率为300πrad/s,则该信号的周期T为( )s。”相关问题
-
第1题:
若周期信号f(t)是时间t的奇函数,则其三角形傅里叶级数展开式中()。A.没有余弦分量
B.既有正弦分量和余弦分量,又有直流分量
C.既有正弦分量和余弦分量
D.仅有正弦分量
正确答案:D
-
第2题:
下列( )是周期为T的非正弦信号可以分解为傅里叶级数的条件。A.满足狄利赫利条件
B.频谱是连续的
C.必须平均值为零
D.频谱是断续的答案:A解析:周期为T的非正弦信号可以分解为傅里叶级数的条件是满足狄利赫利条件。 -
第3题:
一个非正弦周期信号,利用傅里叶级数展开一般可以分解为( )。A.直流分量
B.基波分量
C.振幅分量
D.谐波分量答案:A,B,D解析:非正弦周期信号,利用傅里叶级数展开为:直流分量、基波均量、谐波分量。 -
第4题:
()是指对周期性非正弦交流量进行傅里叶级数分解所得到的大于基波频率整数倍的各次分量。
A谐波
B基波
C偶次谐波
D奇次谐波
A
略 -
第5题:
工频电流的频率f=()Hz,周期T=()s,角频率ω=()rad/s
正确答案:50;0.02;314 -
第6题:
某周期为0.02s的非正弦周期信号,分解成傅立叶级数时,角频率为300p rad/s的项称为()。
- A、三次谐波分量
- B、六次谐波分量
- C、基波分量
正确答案:A -
第7题:
一个正弦交流电的周期是0.02秒;则其频率为角频率ω为314rad/s。
正确答案:正确 -
第8题:
所谓谐波分析,就是对一个已知()的非正弦周期信号,找出它所包含的各次谐波分量的()和(),写出其傅里叶级数表达式的过程。
正确答案:波形;振幅;频率 -
第9题:
某周期为0.02s的非正弦周期信号,分解成傅里叶级数时,角频率为300πrad/s的项称为()。
- A、三次谐波分量
- B、六次谐波分量
- C、基波分量
- D、高次谐波分量
正确答案:A -
第10题:
单选题某周期为T的非正弦周期信号分解为傅里叶级数时,其三次谐波的角频率为300nrad/s,则该信号的周期T为()S。A50
B0.06
C0.02
D不确定
正确答案: C解析: 暂无解析 -
第11题:
单选题周期为丁的非正弦信号可以分解为傅里叶级数的条件为()。A满足狄利赫利条件
B无条件
C必须平均值为零
正确答案: A解析: 暂无解析 -
第12题:
填空题已知某周期信号的周期为0.2s,则该信号的3次谐波分量的频率为()Hz。正确答案: 15解析: 暂无解析 -
第13题:
某周期为0.02s的非正弦周期信号,分解成傅里叶级数时,角频率为300πrad/s的项被称为( )。A.三次谐波分量
B.六次谐波分量
C.基波分量
D.五次谐波分量答案:A解析: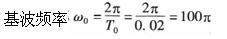
-
第14题:
某方波信号的周期T=5μs,则此方波的三次谐波频率为( )。 答案:C解析:
答案:C解析: -
第15题:
关于谐波分析,下列说法正确的是( )A.一个非正弦周期波可分解为无限多项谐波成分,这个分解的过程称为谐波分析
B.谐波分析的数学基础是傅里叶级数
C.所谓谐波分析,就是对一个已知波形的非正弦周期信号,找出它所包含的各次谐波分量的振幅和频率,写出其傅里叶级数表达式的过程
D.方波的谐波成分中只含有正弦成分的各偶次谐波答案:A,B,C解析:谐波分析的数学基础是傅里叶级数,将非正弦周期信号分解为无限多项谐波成分、基波分量和直流分量。方波的谐波成分中有奇、偶次谐波。谐波分析即求解各次谐波分量的振幅和频率。 -
第16题:
某方波信号的周期T=5μs,则此方波的三次谐波频率为()
- A、106Hz
- B、23106Hz
- C、63105Hz
正确答案:C -
第17题:
已知某周期信号的周期为0.2s,则该信号的3次谐波分量的频率为()。
正确答案:15Hz -
第18题:
一个非正弦周期波可分解为无限多项谐波成分,这个分解的过程称为(),其数学基础是傅里叶级数。
正确答案:谐波分析 -
第19题:
若周期信号f(t)是周期偶函数,则其傅氏级数中只有偶次谐波
正确答案:错误 -
第20题:
周期为丁的非正弦信号可以分解为傅里叶级数的条件为()。
- A、满足狄利赫利条件
- B、无条件
- C、必须平均值为零
正确答案:A -
第21题:
对于一个非正弦的周期量,可利用傅里叶级数展开为各种不同频率的正弦分量与直流分量,其中角频率等于ωt的称为基波分量, 角频率等于或大于2ωt的称为高次谐波。
正确答案:正确 -
第22题:
单选题如下不正确的描述是()。A满足狄里赫利条件的周期信号可描述为傅里叶级数形式
B满足狄里赫利条件的周期信号可分解为一系列谐波分量
C满足狄里赫利条件的周期信号的频谱是离散的频谱
D满足狄里赫利条件的周期信号的谱线密度与周期信号的周期无关
正确答案: D解析: 暂无解析 -
第23题:
单选题某周期为0.02s的非正弦周期信号,分解成傅里叶级数时,角频率为300πrad/s的项称为()。A三次谐波分量
B六次谐波分量
C基波分量
D高次谐波分量
正确答案: A解析: 暂无解析
