某企业资料如下：(1)定量判断产量与单位产品成本间的相关系数;(2)用最小二乘法建立线性回归方程，并说明回归系数的经济含义;(3)计算估计标准误差(以上问题均保留四位小数)。

题目

某企业资料如下：

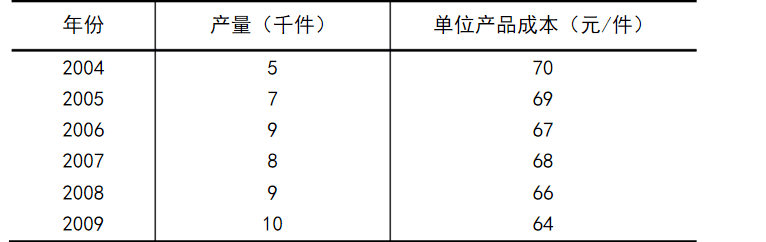
(1)定量判断产量与单位产品成本间的相关系数;

(2)用最小二乘法建立线性回归方程，并说明回归系数的经济含义;

(3)计算估计标准误差(以上问题均保留四位小数)。

相似考题

1.一元线性回归方程中的两个待定系数1β与2β的估计值，一般要用最小二乘法作出估计。此题为判断题(对，错)。

2.通常以测得的响应信号与被测浓度作图，用最小二乘法进行线性回归，求出回归方程和相关系数，需用至少()个不同浓度的样品A、2B、3C、5D、10

3.产量（X，台）与单位产品成本（Y，元/台）之间的回归方程为Y=365-2X，这说明（）。A.产品产量每增加1台，单位产品成本减少2元B.产品产量每增加1台，单位产品成本增加2元C.产品产量每增加1台，单位产品成本减少365元D.产品产量每增加1台，单位产品成为增加365元

4.设单位产品成本(元)对产量(千件)的一元线性回归方程为ŷ=67－4.2x,这表示( )。A. 产量为1000件时，单位产品成本为67元B. 产量为1000件时，单位产品成本为62.8元C. 产量每增加1000件时，单位产品成本下降67元D. 产量每增加1000件时单位产品成本下降62.8元

更多“某企业资料如下:(1)定量判断产量与单位产品成本间的相关系数;(2)用最小二乘法建立线性回归方程 ”相关问题

  • 第1题：

    下列关于回归方程的显著性检验的说法正确的有（ ）。
    A.检验两个变量间是否存在线性相关关系的问题便是对回归方程的显著性检验问题
    B.建立回归方程的目的是表达两个具有线性相关的变量间的定量关系，因此只有当两个变量间具有线性关系，即回归是显著的，这时建立的回归方程才是有意义的
    C.求两个变量间相关系数，对于给定的显著水平，仅当相关系数r的绝对值大于临界值r1-a/2(n-2)时，便认为两个变量间存在线性相关关系，所求得的回归是显著的，即回归方程是有意义的
    D.为了推广到多元线性回归场合，另一种检验方法是方差分析的方法
    E.当SR，SE，fA，fE已知，对于给定的显著性水平a，F1-a(fA，fE)时，认为回归方程显著，即是有意义的


    答案：A,B,C,D
    解析：
    E项，当SR，SE，fA，fE已知，对于给定的显著性水平a，F>F1-a(fA，fE)时，认为回归方程显著，即是有意义的。

  • 第2题：

    某工厂生产的某种产品的产量与单位成本的数据如下：



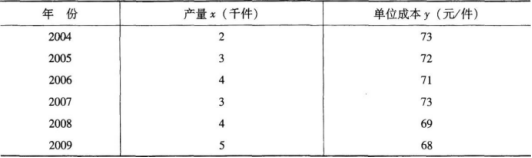
    要求：(1)计算相关系数r；
    (2)建立产量对单位成本的直线回归方程，并解释斜率的经济学意义；
    (3)该工厂计划2010年大幅度提高产量，计划产量达到7000件，则单位成本将为多少?


    答案：
    解析：
    先列出计算表：



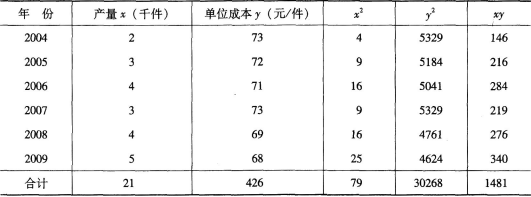
    (1)



    计算结果表明产量与单位成本高度负相关。
    (2)确定直线回归方程：



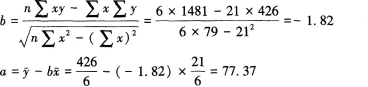
    直线回归方程为y=77．37-1．82x
    斜率即回归系数b=-1．82的经济意义，该产品的产量每增加1千件，则该产品的生产成本将平均降低1．82元。
    (3)将销售额7000件代人回归方程，算得y=77．37-1．82×7=64．63
    即当产量达到7000件的时候，产品的生产成本会降低到64．63元。

  • 第3题：

    2、数据1.sav中。 （1）判断年龄与收入间相关性和相关系数，2个变量间能否构造线性回归方程？为什么？ （2）如果可以的话，试构造线性回归方程，判断回归直线的拟合度。（ps：该数据为2002年调查数据，年龄以2002年为基准）（α＝0.05） （3）结合相关理论和观点，对统计结果进行解释（统计结果说明了什么问题，反应了什么社会现象） 注意：请在答案中附上SPSS输出结果的对应代码。


    对

  • 第4题：



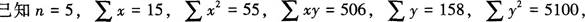
    (1)计算相关系数；
    (2)建立直线回归方程。


    答案：
    解析：
    (1)相关系数：



    (2)



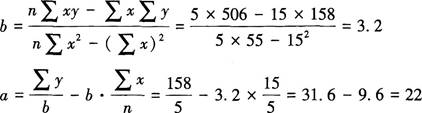
    直线回归方程为：y=22+3．2x

  • 第5题：

    产量（X，台）与单位产品成本（Y，元/台）之间的回归方程为Y=362-2X，这说明（）。

    A.产品产量每增加1台，单位产品成本减少2元
    B.产品产量每增加1台，单位产品成本增加2元
    C.产品产量每增加1台，单位产品成本减少365元
    D.产品产量每增加1台，单位产品成本增加365元

    答案：A
    解析：
    本题考查的是运筹学中的线性规划，正确选项为A产品产量每增加1台，单位产品成本减少2元。
    产量X，单位产品成本Y，回归方程为Y=362-2X，X增加1，Y减少2，X越大Y越小，所以就是产品产量每增加1台，单位产品成本减少2元。

相关内容