设条件甲为：0A.乙是甲的充分条件，但不是甲的必要条件． B.乙是甲的必要条件，但不是甲的充分条件． C.乙是甲的充要条件． D.乙不是甲的充分条件，也不是甲的必要条件．
题目
设条件甲为：0
A.乙是甲的充分条件，但不是甲的必要条件．
B.乙是甲的必要条件，但不是甲的充分条件．
C.乙是甲的充要条件．
D.乙不是甲的充分条件，也不是甲的必要条件．
B.乙是甲的必要条件，但不是甲的充分条件．
C.乙是甲的充要条件．
D.乙不是甲的充分条件，也不是甲的必要条件．
相似考题
更多“设条件甲为：0A.乙是甲的充分条件，但不是甲的必要条件． B.乙是甲的必要条件，但不是甲的充分条件． C.乙是甲的充要条件． D.乙不是甲的充分条件，也不是甲的必要条件．”相关问题
-
第1题：
假设“如果甲是经理且乙不是经理。那么丙是经理”为真．由以下哪个前提可推出“乙是经理”的结论?（）
A.甲和丙都不是经理
B.甲和丙都是经理
C.甲不是经理，丙是经理
D.甲是经理．丙不是经理答案：D解析：题干假设是一个充分条件的假言命题，要推出“乙是经理”，即要否定前件，由否定后件则否定前件可知，需否定后件，即要求“丙不是经理”作为前提．而由否定的后件可以得到否定的前件，即甲不是经理或者乙是经理。进而要推出“乙是经理”的结论。需要否定另一个选言肢“甲不是经理”，即要求“甲是经理”作为前提。故正确答案是D。 -
第2题：
甲、乙、丙、丁四人的职业是：教师、医生、设计师、演员。其中：
(1)甲不是教师，也不是演员。
(2)乙不是设计师，也不是教师。
(3)如果甲不是设计师，那么丁不是教师。
(4)丙不是演员，也不是教师。
根据以上陈述．可知下列哪项为真?A: 甲是设计师，乙是医生
B: 丙是教师．丁是演员
C: 甲是设计师，丁是医生
D: 乙是演员．丙是医生答案：D解析：由(1)(2)(4)可知，甲、乙、丙都不是教师’，所以教师是丁。由(3)可知，
甲是设计师。再由(4)丙不是演员可知，丙应该是医生，故乙是演员。答案为D。 -
第3题：
命题甲：lgx，lgy，lgz成等差数列；命题乙：y2＝x·z则甲是乙的（）A.充分而非必要条件
B.必要而非充分条件
C.既充分又必要条件
D.既非充分也非必要条件答案：A解析：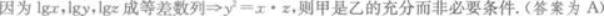
-
第4题：
命题甲：实数a，b，c成等比数列；命题乙：b2＝ac，则甲是乙（ ）A.充分条件但不是必要条件
B.必要条件但不是充分条件
C.充分必要条件
D.不是充分条件也不是必要条件答案：A解析：
-
第5题：
设甲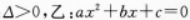
有两个不相等的实数根，则( )A.甲是乙的必要条件，但不是充分条件
B.甲是乙的充分条件，但不是必要条件
C.甲是乙的充分必要条件
D.甲不是乙的充分条件，也不是必要条件答案：C解析：【考情点拨】本题主要考查的知识点为简易逻辑． 【应试指导】
有两个不相等的实数根． -
第6题：
若甲：x>1；乙：ex>1，则（ ）A.甲是乙的必要条件，但不是乙的充分条件
B.甲是乙的充分必要条件
C.甲不是乙的充分条件，也不是乙的必要条件
D.甲是乙的充分条件，但不是乙的必要条件答案：D解析： -
第7题：
［0202］设甲：x>3，乙：x>5，则（）A.甲是乙的充分条件，但不是乙的必要条件
B.甲是乙的必要条件，但不是乙的充分条件
C.甲是乙的充分必要条件
D.甲不是乙的充分条件，也不是乙的必要条件答案：B解析： -
第8题：
甲、乙、丙和丁是同班同学。
甲说：“我班同学都是团员。”
乙说：“丁不是团员。”
丙说：“我班有人不是团员。”
丁说：“乙也不是团员。”
已知只有一个人说假话，则可推出以下判定肯定是真的一项为（ ）。A.说假话的是甲，乙不是团员
B.说假话的是乙，丙不是团员
C.说假话的是丁，乙不是团员
D.说假话的是甲，丙不是团员答案：A解析：A -
第9题：
甲是乙的必要条件,丙是乙的充分条件但不是乙的必要条件，那么_____。A.丙是甲的充分条件但不是甲的必要条件
B.丙是甲的必要条件但不是甲的充分条件
C.丙是甲的充分必要条件
D.丙既非甲的充分条件，又非甲的必要条件答案：A解析：由“甲是乙的必要条件”可知：甲—乙；由“丙是乙的充分条件”可知：丙—乙；因此可得： 丙―乙—甲；但由甲不能推出丙，故丙是甲的充分条件但不是甲的必要条件。故答案选A。 -
第10题：
单选题设甲：x＝1，乙：x2＝1，则（ ）．A甲是乙的必要条件，但不是乙的充分条件
B甲是乙的充分必要条件
C甲是乙的充分条件，但不是乙的必要条件
D甲既不是乙的充分条件，也不是乙的必要条件
正确答案： D解析：
由题意可知，x＝1→x2＝1；反之，x2＝1→x＝±1． -
第11题：
单选题已知p是r的充分条件而不是必要条件，q是r的充分条件，s是r的必要条件，q是s的必要条件，现有下列命题：①s是q的充要条件；②p是q的充分条件而不是必要条件；③r是q的必要条件而不是充分条件；④﹁p是﹁s的必要条件而不是充分条件；⑤r是s的充分条件而不是必要条件。则正确命题的序号是（ ）。A①④⑤
B①②④
C②③⑤
D②④⑤
正确答案： D解析：
由“q是r的充分条件”和“s是r的必要条件”可以得到“q是S的充分条件”，又由于“q是s的必要条件”可知“s是q的充要条件”，①成立；由“p是r的充分条件”和“s是r的必要条件”可以得到“p是s的充分条件”，又由“q是s的必要条件”可以得到“p是q的充分条件”，但得不到“p是q的必要条件”，所以②成立；由“q是r的充分条件”、“s是r的必要条件”和“q是s的必要条件”可以得到“r是q的充要条件”，③不成立；因为“p是s的充分条件但不是必要条件”是真命题，那么逆否命题也是真命题，即“﹁p是﹁s的必要条件而不是充分条件”正确，④成立；由“q是r的充分条件”、“s是r的必要条件”和“q是s的必要条件”可以得到“r是s的充要条件”，⑤不成立。 -
第12题：
甲、乙、丙、丁四人的职业是：教师、医生、设计师、演员。其中，（1）甲不是教师，也不是演员。 （2）乙不是设计师，也不是教师。 （3）如果甲不是设计师，那么丁不是教师。 （4）丙不是演员，也不是教师。
根据以上陈述，可知下列哪项为真？A.甲是设计师，乙是医生
B.丙是教师，丁是演员
C.甲是设计师，丁是医生
D.乙是演员，丙是医生答案：D解析：第一步，确定题型。
题干有明显的信息匹配特征，确定为分析推理。
第二步，分析条件，进行推理。
翻译题干：①?甲教师且?甲演员
②?乙设计师且?乙教师
③?甲设计师→?丁教师
④?丙演员且?丙教师
根据以上信息，优先使用最大信息法，先确定教师是谁，根据①②④可知甲、乙、丙都不是教师，那么丁是教师；
“丁是教师”是对③的“否后”，根据“否后必否前”，可得甲是设计师；
因此，还剩演员和医生的身份没确定，由④可知丙不是演员，因此丙是医生，而乙是演员。 -
第13题：
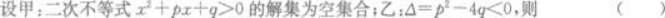A.甲是乙的必要条件，但不是乙的充分条件
B.甲是乙的充分条件，但不是乙的必要条件
C.甲不是乙的充分条件，也不是乙的必要条件
D.甲是乙的充分必要条件答案：D解析：
-
第14题：
已知两条异面直线m；n，且m在平面α内，n在平面β内，设甲：m//β，n//α；乙：平面α//平面β，则（ ）A.甲为乙的必要但非充分条件
B.甲为乙的充分但非必要条件
C.甲非乙的充分也非必要条件
D.甲为乙的充分必要条件答案：D解析：两条异面直线m，n，且m在平面α内，n在平面β内，因为m//β，n//α←→平面α∥平面β，则甲为乙的充分必要条件．(答案为D) -
第15题：
设甲：a＞0且b＞0；乙：ab＞0，则甲是乙的（ ）A.充分条件，但非必要条件
B.必要条件，但非充分条件
C.既非充分条件，也非必要条件
D.充分必要条件答案：A解析：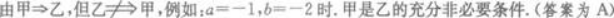
-
第16题：
[0402]设甲：四边形ABCD是平行四边形，乙：四边形ABCD是正方形，则（ ）A.甲是乙的充分条件，但不是乙的必要条件
B.甲是乙的必要条件，但不是乙的充分条件
C.甲是乙的充分必要条件
D.甲不是乙的充分条件，也不是乙的必要条件答案：B解析： -
第17题：
设命题甲：x+1=0，命题乙：x2-2x-3=0，则（）。A.甲是乙的充分条件，但不是乙的必要条件
B.甲是乙的必要条件，但不是乙的充分条件
C.甲是乙的充分必要条件
D.甲不是乙的必要条件，也不是乙的充分条件答案：A解析： -
第18题：
以“甲和乙不都是律师”为前提，再增加（ ）为一个前提，就可以有效地推出结论“乙不是律师”。
A.甲是律师 B.如果甲不是律师，则乙是律师
C.甲不是律师 D.如果甲是律师，则乙不是律师答案：A解析：本题考查逻辑学，所给前提结合“甲是律师”，可以推出结论“乙不是律师”。 -
第19题：
甲是乙的必要条件，丙是乙的充分条件但不是乙的必要条件，那 么_。A.丙是甲的充分条件但不是甲的必要条件
B.丙是甲的必要条件但不是甲的充分条件
C.丙是甲的充分必要条件
D.丙既非甲的充分条件，又非甲的必要条件答案：A解析：由“甲是乙的必要条件”可知：甲—乙；由“丙是乙的充分条件”可知：丙—乙；因此可得： 丙—乙—甲；但由甲不能推出丙，故丙是甲的充分条件但不是甲的必要条件。故答案选A。 -
第20题：
设“甲和乙都不是美国人”、“若甲不是美国人，则：是美国人”和“乙不是美国人，而甲是美国人”这三个判断中只有一个为假，则可必然推出下列判断中为真的是（）。
- A、“甲和乙都是美国人”
- B、“甲是而乙不是美国人”
- C、“甲不是而乙是美国人”
- D、“甲和乙都不是美国人”
正确答案:B -
第21题：
单选题已知a，b，c∈R，命题甲为“a＞b”，命题乙为“ac4＞bc4”，那么（ ）．A甲是乙的充分条件，但不是必要条件
B甲是乙的必要条件，但不是充分条件
C甲是乙的充分必要条件
D甲既不是乙的充分条件，也不是乙的必要条件
正确答案： C解析：
由命题甲不能得到命题乙，因为当c＝0时，结论就不成立；由命题乙可以得到命题甲，因为由乙可知c≠0，所以c4＞0，从而得到命题甲成立． -
第22题：
单选题设甲：2a＞2b，乙：a＞b，则（ ）．A甲是乙的必要条件，但不是乙的充分条件
B甲是乙的充分条件，但不是乙的必要条件
C甲不是乙的充分条件，也不是乙的必要条件
D甲是乙的充分必要条件
正确答案： B解析：
由于y＝2x是（－∞，＋∞）内的增函数，所以2a＞2b等价于a＞b．即甲是乙的充分必要条件．