某类灯泡使用时数在1000小时以上的概率为0.2,三个灯泡在使用1000小时以后最多只有一个坏的概率为( )A.0.008 B.0.104 C.0.096 D.1
题目
B.0.104
C.0.096
D.1
相似考题
更多“某类灯泡使用时数在1000小时以上的概率为0.2,三个灯泡在使用1000小时以后最多只有一个坏的概率为( )”相关问题
-
第1题:
抽样方案的接收概率为95%,表示( )。
A.交检100个产品,可接收95个
B.该批产品被接收的概率为95%
C.所交检的每个产品被接收的概率为95%
D.使用此方案的概率为95%
正确答案:B
解析:根据规定的抽检方案,把具有给定质量水平的交检批判为接收的概率称为接收概率。接收概率户。是用给定的抽样方案验收某交检批,其结果为该批产品被接收的概率。 -
第2题:
某企业只生产一种产品,单价、单位变动成本、销售量和固定成本都是不确定因素。在按照联合概率法进行概率分析时,已知在一种组合下,单价的概率为0.4,单位变动成本的概率为0.2,销售量的概率为0.5,固定成本的概率为0.8。则计算该组合下加权的保本量所依据的联合概率应等于()
A、0.032
B、0.5
C、0.064
D、4
参考答案:C
-
第3题:
小浦家电话在家中有人时,打进的电话响第一声时被接的概率为0.1,响第二声时被接的概率为0.2,响第三声时被接的概率为0.4,响第四声时被接的概率为0.2,那么电话在响前4声内被接的概率是多少?( )
A.0.0016
B.0.2
C.0.9
D.1
正确答案:C
根据生活中的经验可知,电话在响4声内,每次声响是否被接听互相不影响,因此它们是和的关系,概率P=0.1+0.2+0.4+0.2=0.9,C项正确。本题易错选A项,
P=0.1×0.2×0.4×0.2=0.0016,错在将和事件当做了积事件。 -
第4题:
电灯泡耐用时间在1000小时以上的概率为0.2,求三只灯泡使用l000小时以后恰有一只坏与最多只有一只坏的概率.答案:解析:

-
第5题:
某次考试小明全对的概率为80%,小宁全对的概率为70%,那么这次考试只有一人全对的概率为多少?A.0.24
B.0.38
C.0.56
D.0.94答案:B解析:第一步,本题考查概率问题中的分类分步型。
第二步,根据题意可知小明做对小宁做错的概率是80%×30%=24%;小宁做对小明做错的概率是70%×20%=14%。
第三步,故只一个人全对的概率为24%+14%=38%。 -
第6题:
小明骑车上学,要经过三个路口,已知在第一个路口遇见红灯的概率为1/3。若前一个路口遇见红灯,则下一个路口遇见红灯的概率为1/2 ;若前一个路口不遇见红灯,则下一个路口遇见红灯的概率为1/4。问小明连续两天都是遇见两个红灯的概率约是多少?
A.0.027
B.0.034
C.0.043
D.0.05答案:C解析: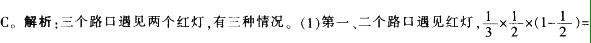
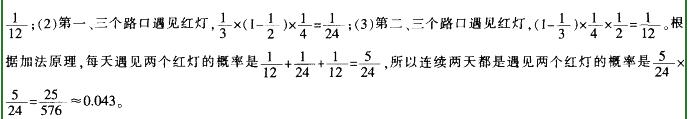
-
第7题:
速算比赛,小李全对的概率为95%,小杨全对的概率为92%,问这次比赛两人中只有一个人全对的概率为:
- A、0.046
- B、0.076
- C、0.122
- D、0.874
正确答案:C -
第8题:
在含量为n的二项分布中,Q(x)表示的含义是()
- A、最多有x例阳性的概率
- B、至少有x例阳性的概率
- C、恰巧有x例阳性的概率
- D、恰巧有n-x例阳性的概率
- E、以上都不对
正确答案:C -
第9题:
设某种动物有出生起活20岁以上的概率为80%,活25岁以上的概率为40%.如果现在有一个20岁的这种动物,问它能活25岁以上的概率()
- A、0.25
- B、0.5
- C、0.6
- D、0.75
正确答案:B -
第10题:
单选题10个灯泡中5个是好的,5个是坏的,混合在一起:(1)若随机有放回的抽取3个灯泡,这3个全是好的概率为多少?(2)如果一开始采用不放回的抽样,抽中3个全是好的概率为多少?正确答案: A解析: -
第11题:
单选题两只相同灯泡在并联使用时,电源电压等于灯泡的额定电压U,现在两只灯泡串联使用,要使灯泡在其额定电压下工作,电源电压为()。A1U
B2U
C3U
D4U
正确答案: D解析: 暂无解析 -
第12题:
单选题某设备使用10年的概率为0.8,能使用15年的概率为0.4,现已使用了10年的设备能继续使用5年的概率为()。A0.5
B0.4
C0.8
D0.2
正确答案: A解析: 条件概率:0.4÷0.8=0.5 -
第13题:
某种灯泡能用到3000小时以上的概率为0.8,能用到3500小时以上的概率为0.7,则一只已用到3000小时仍没有损坏的这种灯泡还可以用500小时以上的概率为?参考答案:P(A)=0.8,P(B)=0.7,P(AB)=P(B),∴P(B|A)=0.7/0.8=7/8
-
第14题:
电灯泡使用时数在1000小时以上的概率为0.2,求三个灯泡在1000小时以后最多有一个坏了的概率()
A、0.7
B、0.896
C、0.104
D、0.3
参考答案:C
-
第15题:
小浦家电话在家中有人时,打进的电话响第一声时被接的概率为0.i,响第二声时被接的概率为0.2,响第三声时被接的概率为0.4,响第四声时被接的概率为0.2,那么电话在响前4声内被接的概率是多少?( )
A.O.0016
B.0.2
C.0.9
D.1
正确答案:C
-
第16题:
速算比赛,小李全对的概率为95%,小杨全对的概率为92%,问这次比赛两人中只有一个人全对的概率为:
A0.046
B0.076
C0.122
D0.874答案:C解析:
-
第17题:
设每次试验成功的概率为0.2,失败的概率为0.8,设独立重复试验直到成功为止的试验次数为X,则E(X)=_______.答案:1、5解析: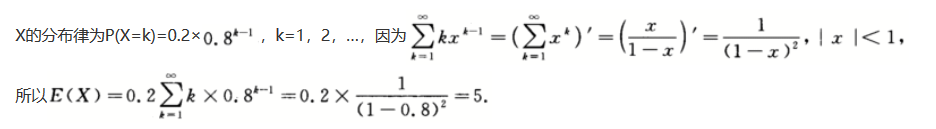
-
第18题:
对某厂日产10000个灯泡的使用寿命进行抽样调查,抽取100个灯泡,测得其平均寿命为1800小时,标准差为6小时。要求: (1)按68.27%概率计算抽样平均数的极限误差; (2)按以上条件,若极限误差不超过0.4小时,应抽取多少只灯泡进行测试; (3)按以上条件,若概率提高到95.45%,应抽取多少灯泡进行测试? (4)若极限误差为0.6小时,概率为95.45%,应抽取多少灯泡进行测试? (5)通过以上计算,说明极限误差、抽样单位数和概率之间的关系。
正确答案: (1)极限误差为0.6小时
(2)应抽取225只灯泡进行测试
(3)应抽取900只灯泡进行测试
(4)应抽取400只灯泡进行测试
(5)极限误差大小、抽样单位数的多少和概率保证程度成正比关系。 -
第19题:
某公司正在考虑在两个项目之间作出选择,X项目净现值为-350000元的概率为0.6,净现值为3000000元的概率为0.2,净现值为5000000元的概率为0.2,X项目的预期净现值为()。
- A、1390000元
- B、7210000元
- C、800000元
- D、679000元
正确答案:A -
第20题:
某公司对两个互斥项目进行评价。其中一个项目的净现值为-400000元的概率为0.7,净现值为1500000元的概率为0.2,净现值为5000000元的概率为0.1,该项目净现值的期望值为()。
- A、520000元
- B、1080000元
- C、800000元
- D、6100000元
正确答案:A -
第21题:
某设备使用10年的概率为0.8,能使用15年的概率为0.4,现已使用了10年的设备能继续使用5年的概率为()。
- A、0.5
- B、0.4
- C、0.8
- D、0.2
正确答案:A -
第22题:
单选题速算比赛,小李全对的概率为95%,小杨全对的概率为92%,问这次比赛两人中只有一个人全对的概率为:A0.046
B0.076
C0.122
D0.874
正确答案: A解析: -
第23题:
单选题故障模式发生的概率等级一般可分为A、B、C、D、E五个等级,其中A等级是指( )。A经常发生,产品在工作期间发生的概率是很高的,即一种故障模式发生的概率大于总故障概率的0.1~0.2
B经常发生,产品在工作期间发生的概率是很高的,即一种故障模式发生的概率大于总故障概率的0.2
C偶然发生,产品在工作期间发生故障是偶然的,即一种故障模式发生的概率为总故障概率的0.01~0.1
D很少发生,产品在工作期间发生故障的概率是很小的,即一种故障模式发生的概率为总故障概率的0.001~0.01
正确答案: D解析:
故障模式发生的概率等级一般可分为:①A级,产品在工作期间发生的概率是很高的,即一种故障模式发生的概率大于总故障概率的0.2;②B级,产品在工作期间发生故障的概率为中等,即一种故障模式发生的概率为总故障概率的0.1~0.2;③C级,产品在工作期间发生故障是偶然的,即一种故障模式发生的概率为总故障概率的0.01~0.1;④D级,产品在工作期间发生故障的概率是很小的,即一种故障模式发生的概率为总故障概率的0.001~0.01;⑤E级,产品在工作期间发生故障的概率接近于零,即一种故障模式发生的概率小于总故障概率的0.001。
